複素関数グラフのワークブック「複素関数5.xls」のダウンロード下記のワークブック「複素関数5.xls」をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「複素関数5.xls」をダウンロードする。ワークブック「複素関数5.xls」説明- ワークブック「複素関数5.xls」は複素関数機能を使用しています。
- 複素関数機能を使うには、メニューの「ツール(T)」＿「アドイン(I)」を選択し、アドインリストの「分析ツール」にチェックマークを設定する必要があります。
- 「複素関数5.xls」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
- シート「操作」はパラメータの設定と操作を行います。
- シート「Yｒ」は関数Yの実数部３Dグラフです。
- シート「Yi」は関数Yの虚数部３Dグラフです。
シート「操作」- Xｒ分割数 Nr：変数Xの実数部範囲の分割数を設定します。
- Xｒ初期値 Xr1：変数Xの実数部の初期値を設定します。
- Xr終値 Xr2：変数Xの実数部の終値を設定します。
- Xi分割数 Ni：変数Xの虚数部範囲の分割数を設定します。
- Xi初期値 Xi1：変数Xの虚数部の初期値を設定します。
- Xi終値 Xi2：変数Xの虚数部の終値を設定します。
- 定数 A：関数Y=A*X^nの係数を設定します。
- 累乗 X^n：=IMPOWER(C16,2)の累乗値2を変更します。
- 「計算実行」ボタンを押すと３Dグラフを作成します。
デフォルト条件での実行結果複素関数Y=X^2の実数部３Dグラフを図5-1に示します。
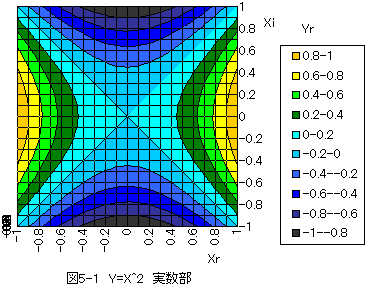
複素関数Y=X^2の虚数部３Dグラフを図5-2に示します。
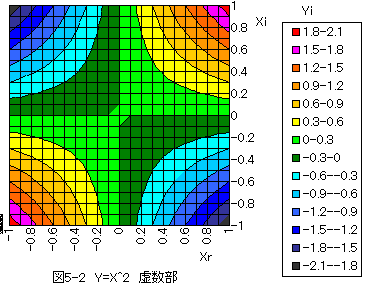
複素関数Y=X^2の微分複素関数Y=X^2の微分はdY/dX＝2Xです。
Yの変化量ΔYはXが実数軸上で変化した場合、すなわち
X＝1、ΔX=0.1の時
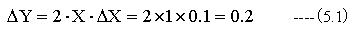
Yの変化量ΔYはXが虚数軸上で変化した場合、すなわち
X＝i、ΔX=0.1×iの時
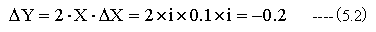
(5.1)式と（5.2）式の計算結果は、図5-1の実数部結果と良く一致していることがわかります。
図5-1において、X＝1の時Yはプラスに変化します。X=Iの時はYはマイナスに変化します。
X=1+i、 ΔX=0.1×（1+i）の時
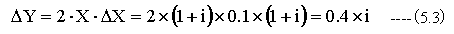
となり、Yの虚数部がプラスに変化することがわかります。この結果は図5-2の虚数部の結果と良く一致します。
トリックのような複素関数の微分公式は、ＥＸＣＥＬの複素関数機能で計算した３Ｄグラフの結果と良く一致します。
６章：複素指数関数に行く。