複素関数の不定積分複素関数も実数の関数と全く同様に不定積分することが可能です。
一般に関数F(X)の微分関数がｆ（X)であるとき、F(X)をｆ（X)の原始関数といいます。
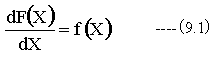
一般に関数ｆ（X)の原始関数がF(X)であるならば、すべての原始関数G(X)はF(X)+Cで表すことができます。ここにCは定数を表します。
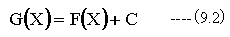
関数ｆ（X)の原始関数を表すに
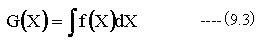
なる記号を用いる。例えば
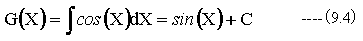
また、X＾3の微分関数は3X^2であるから
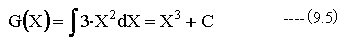
和の原始関数U,VをXの関数、A,Bを定数とすれば
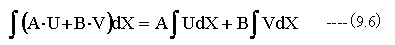
置換積分法ｆ（X)をXの関数とし、
とおくならば
今、Xを変数ｔの関数U(t)で置き換える。すなわち、X=U(t)なる置換を行う。すると、ｆ（X)はｔの関数となり、従ってGもtの関数となる。
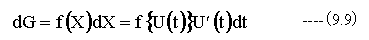
これを積分すれば
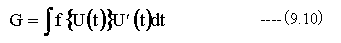
部分積分法U,VをXの関数とすれば
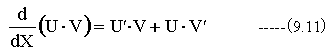
ゆえに積分して
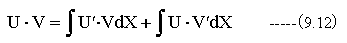
移項して、
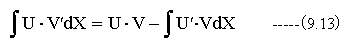
(9.13)式は以下のようにも変形できる。
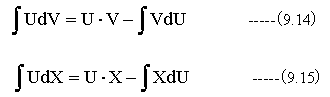
実数での不定積分の公式は上記以外にもたくさんあるが、公式集を参照されたい。
複素関数においても、ほとんど例外なく実数での不定積分の公式がそのまま適用できます。
１０章：複素関数の定積分に行く。