スカラースカラーとは方向を持たず大きさだけを持つ量のことです。スカラー関数は一般に下記式のようになります。
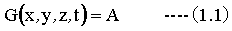
（1.1）式において、x,y,zは3次元の座標です。tは時間であり、Aは任意の実数または複素数です。
ベクトルベクトルとは方向と大きさを持つ量のことです。ベクトル関数は一般に下記式のようになります。
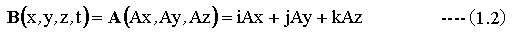
（1.2）式において、x,y,zは3次元の座標です。tは時間であり、Aはベクトルです。Axはベクトルのｘ成分、Ayはベクトルのｙ成分、Azはベクトルのｚ成分です。
i,j,kはベクトルの成分方向を表す記号です。
位置ベクトル位置ベクトルとは、位置を表すベクトルのことで、下記の条件を満たすとき位置ベクトルとなります。
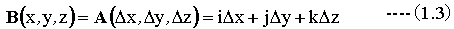
（1.3）式において、x,y,zは3次元の座標です。Δx、Δｙ、Δｚはそれぞれxyx方向の変化量をしめします。
（1.3）式において、 x,y,zはベクトルの始点、x+ Δx 、y+Δｙ、z+Δｚはベクトルの終点となります。この場合、位置ベクトルは相対移動量を表します。
ベクトルの始点を座標原点にした場合は、 Δx、Δｙ、Δｚがベクトルの終点となり、終点がxyz座標値に一致します。
ここでは、相対移動量の位置ベクトルと始点が座標原点の位置ベクトルを区別して、それぞれ「相対位置ベクトル」、「絶対位置ベクトル」と呼ぶことにします。
位置ベクトル以外にも、物理量を表すベクトルもありますので注意する必要があります。
ベクトルの加算と減算2個以上のベクトルは加算または減算が可能です。
ベクトルは加算または減算は下記のように定義されます。
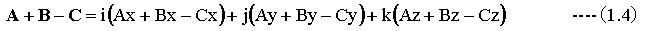
（1.4）式において、ベクトルの加算または減算はそれぞれ、ｘｙｚ成分毎に加算または減算すればよいことを示しています。
位置ベクトルの作図演習EXCELを用いて、位置ベクトルの作図演習を行い、ベクトルの加算のイメージアップを図りましょう!!
ワークブック「ベクトル解析1.xls」のダウンロード下記のワークブック「ベクトル解析1.xls」（ベクトル作図プログラム）をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「ベクトル解析1.xls」をダウンロードする。ワークブック「ベクトル解析1.xls」説明- ワークブック「ベクトル解析1.xls」は複素関数機能を使用していません。
- 「ベクトル解析1.xls」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
- シート「操作」はパラメータの設定と操作を行います。
- シート「XY平面」はXY平面上の作図を行います。
- シート「YZ平面」はYZ平面上の作図を行います。
シート「操作」- ベクトル数(Nb) ：ベクトル数を設定します。
- ΔX：ベクトルのX成分を設定します。
- ΔY：ベクトルのY成分を設定します。
- ΔZ：ベクトルのZ成分を設定します。
- 「作図実行」ボタンを押すと作図を実行します。
作図結果入力条件を下記表に示します。
ベクトル数 Nb＝3
| No | ΔX | ΔY | ΔZ |
| 1 | 20 | 50 | 10 |
| 2 | -60 | -40 | -80 |
| 3 | 40 | -10 | 70 |
作図結果を下記に示します。
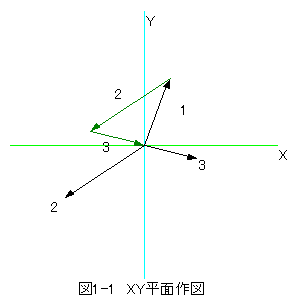
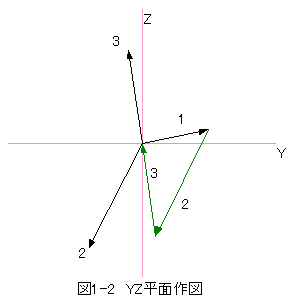
図1-1と図1-2において、黒色の矢印が絶対位置ベクトル、緑色の矢印が相対位置ベクトルです。
絶対位置ベクトルでは3個の矢印が独立していますが、相対位置ベクトルでは逐次ベクトルの加算処理 が行われ、最後に原点に戻っていることが確認できます。
この逐次ベクトルの加算処理は各成分毎に行っており、加算処理の変化を確認できます。（減算は符号をマイナスにするだけです。）
ベクトル数やΔX ΔY ΔZ の値を変化させて、相対位置ベクトルの加算・減算の変化イメージを確認 しましょう。
２章：直線のベクトル方程式に行く。