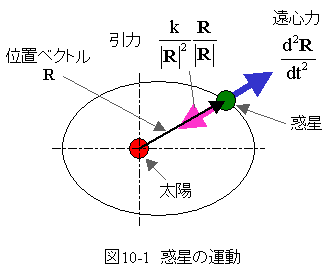
惑星の運動方程式惑星は太陽を中心とし、楕円軌道で運動します。
このとき、太陽からの距離の２乗に反比例した引力を受けます。
また、惑星は楕円軌道で運動することにより遠心力が働きます。
惑星の運動方程式は、引力と遠心力がバランスした下記の方程式となります。
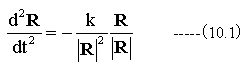
（10.1）式のkは比例定数です。
（10.1）式は簡単な形をしており、すぐ解が求まりそうですが、実際には簡単ではありません。
（10.1）式をX、Y、Z成分に分離して表すと下記のようになります。
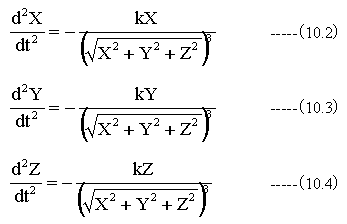
（10.1）式は（10.2）式〜（10.4）式の連立微分方程式を表しています。このような連立微分方程式を代数的に解くのはかなり厄介です。
ルンゲ・クッタ法による数値計算ルンゲ・クッタ法を使用すれば、このような連立微分方程式を容易に計算することができます。
ルンゲ・クッタ法を使用するために以下のように式を変形します。
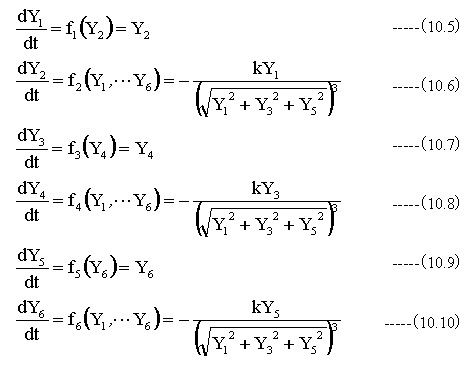
上記の式の変数において下記の関係があります。
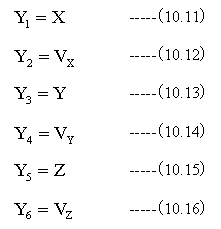
惑星の運動演習EXCELを用いて、惑星の運動演習を行い、惑星の運動のイメージアップを図りましょう!!
ワークブック「ベクトル解析10.xls」のダウンロード下記のワークブック「ベクトル解析10.xls」（ルンゲ・クッタ法プログラム）をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「ベクトル解析10.xls」をダウンロードする。ワークブック「ベクトル解析10.xls」説明- ワークブック「ベクトル解析10.xls」は複素関数機能を使用していません。
- 「ベクトル解析10.xls」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
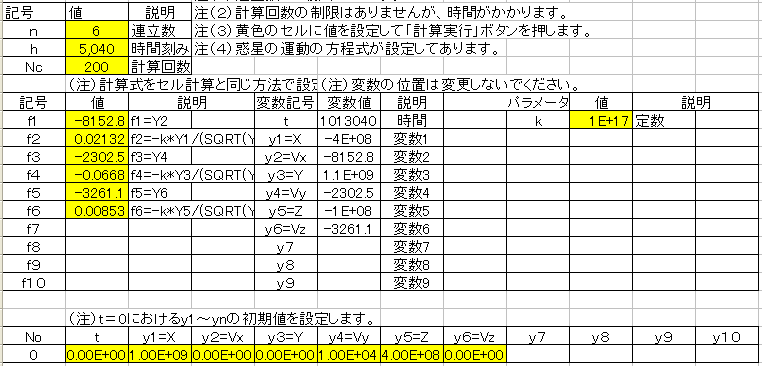
- シート「Sheet1」はパラメータの設定と操作を行います。
- シート「XY平面」はXY平面上のグラフです。
- シート「YZ平面」はYZ平面上のグラフです。
シート「Sheet1」- ｎ 6 連立数 を設定します。
- h 5,040 時間刻み を設定します。
- Nc 200 計算回数 を設定します。
- k 1E+17 定数 を設定します。
- ｆ1 =F12 f1=Y2 を設定します。
- ｆ２ =-J10*F11/(SQRT(F11^2+F13^2+F15^2))^3 f2=-k*Y1/(SQRT(Y1^2+Y3^2+Y5^2))^3 を設定します。
- ｆ３ =F14 f3=Y4 を設定します。
- ｆ４ =-J10*F13/(SQRT(F11^2+F13^2+F15^2))^3 f4=-k*Y3/(SQRT(Y1^2+Y3^2+Y5^2))^3を設定します。
- ｆ５ =F16 f5=Y6 を設定します。
- ｆ６ =-J10*F15/(SQRT(F11^2+F13^2+F15^2))^3 f6=-k*Y5/(SQRT(Y1^2+Y3^2+Y5^2))^3 を設定します。
- ｔ t=0 を設定します。
- ｙ1=X t=0におけるXを設定します。
- ｙ２=Vx t=0におけるVxを設定します。
- ｙ３=Y t=0におけるYを設定します。
- ｙ4=Vy t=0におけるVyを設定します。
- ｙ５=Z t=0におけるZを設定します。
- ｙ６=Vz t=0におけるVzを設定します。
- 「計算実行」ボタンを押すと計算を実行します。
計算結果入力条件を下記表に示します。
グラフを下記に示します。
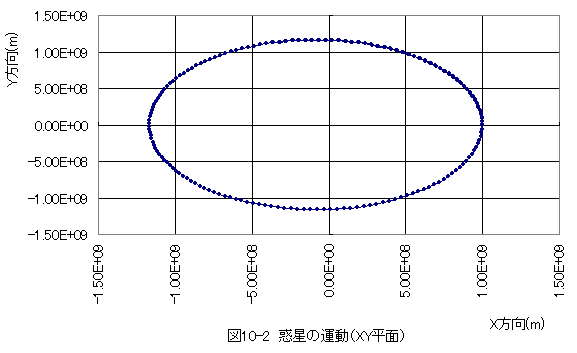
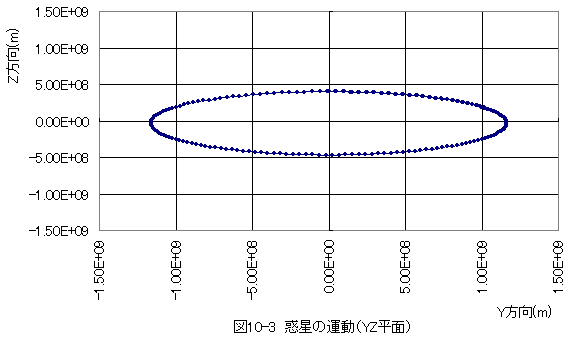
図10-2と図10-3から惑星は楕円軌道となることがわかります。
１１章：引力と重力場に行く。