ベクトルの発散は、電磁気学でよく見かけられる数学記号です。ベクトルの発散の定義と意味を理解する必要があります。
ベクトルの発散の定義ベクトル関数をA(X,Y,Z)とするとき、ベクトルの発散は下記式で定義されます。
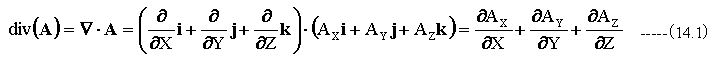
（14.1）式の等号は、全て同じ意味です。ベクトルの発散をdiv(A)書く場合もあれば、▽・Aと書く場合もあります。
具体的な演算は左辺のXYZの各成分の偏微分の和として計算されます。
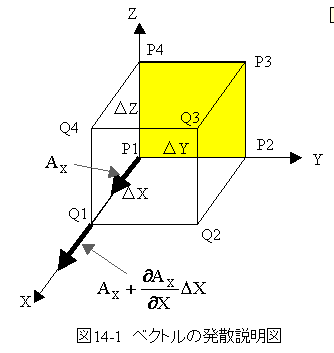
ベクトルの発散の意味図14-1にベクトルの発散説明図を示します。
図14-1において、位置（X,Y,Z)がP1点です。
位置（X+ ΔX,Y,Z)がQ1点、位置（X,Y + ΔY,Z)がP2点、位置（X,Y,Z + ΔZ)がP4点となっています。
また、位置（X,Y,Z)と位置（X+ ΔX,Y,Z)におけるベクトルAのX成分はそれぞれ
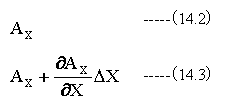
従って、P1,P2,P3,P4,Q1,Q2,Q3Q4で構成される立方体に流れ込むベクトル量と流失するベクトル量はそれぞれ
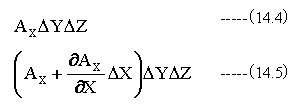
となります。Y,Z方向も同様であり、下記の関係式が成立します。
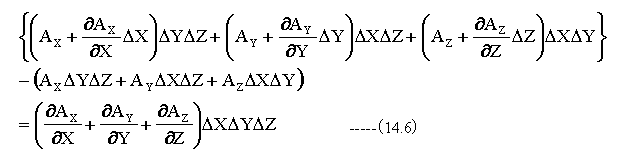
（14.6）式の左辺はベクトルの発散の定義式と一致します。したがって、ベクトルの発散は単位立方体に流れ込むベクトル量と流失するベクトル量の差分を意味しています。
ガウスの発散定理（14.6）式を変形するとガウスの発散定理が得られます。
ベクトルAと面積ベクトルdSの内積は下記式となります。
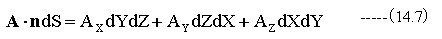
（14.6）式の左辺と（14.7）式は同じ形になっていることに注目する必要があります。 （14.6）式の左辺では立方体に流れ込むベクトル量と流失するベクトル量の差分となっています。
閉曲面Sで囲まれた領域から流失するベクトル量とするならば、単位法線ベクトルは内部から外部に向かうベクトルとし、 （14.7）式を積分を積分します。
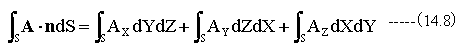
一方、閉曲面Sで囲まれた領域をVとして（14.6）式の右辺を積分すると
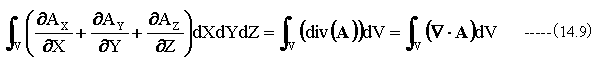
（14.8）式と（14.9）式は等しくなければなりません。従って
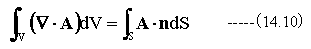
となります。 （14.10）式がガウスの発散定理です。ガウスの発散定理は体積積分が面積積分に置き換えられることを示しています。またその逆も成立します。
グリーンの定理グリーンの定理はガウスの発散定理
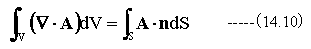
の変形です。
閉曲面Sに囲まれた領域Vにおいて、スカラー点関数φとψが定義されているとします。
ここでベクトルの下記の発散の公式を用います。
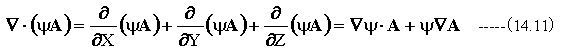
A=▽φの時、（14.11）式は
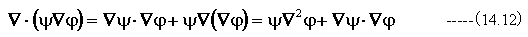
一方
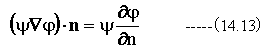
の関係が成立します。（14.10）式に（14.12）式と（14.13）式を代入すると
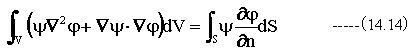
（14.14）式のφとψを入れ替えると
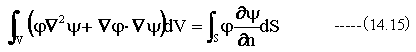
（14.14）式と（14.15）式の差をとると
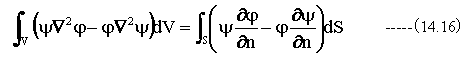
（14.14）式と（14.16）式をグリーンの定理といいます。したがって、グリーンの定理はガウスの発散定理の変形にすぎないことがわかります。
１５章：重力場における発散と地球の重力場に行く。