重力場における発散と地球の重力場ベクトルの発散とガウスの発散定理とグリーンの定理の式の展開をみていると誘導の過程は理解できますが、さっぱりイメージがわきません。
ベクトルの発散のイメージをつかむため、重力場における発散を検討してみましょう。
重力場のポテンシャルエネルギーは下記のスカラー関数となります。
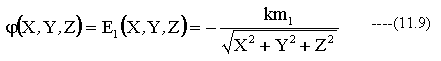
重力場におけるスカラーの勾配（加速度）は方向と大きさを持つベクトルαとなります。この加速度ベクトルαは下記式となります。
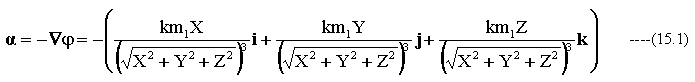
重力場における発散は
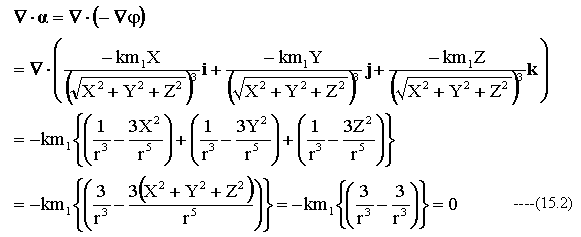
（15.2）式において、記述スペース節約のため
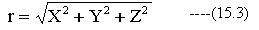
としています。式の展開は複雑ですが、結果的に重力場における発散はゼロとなります。ただし、r=0は特異点であり発散の計算は成立しません。
r=0を除く全ての領域で発散はゼロです。なぜ？このような結果になったかいうと巨大な質量m1が無限小の点に存在すると仮定して、重力場のポテンシャルエネルギーを定義したためです。
このような仮定においては、 、r=0が特異点となります。
質量m1から流出するベクトル量の総和質量m1から流出するベクトル量の総和はガウスの発散定理
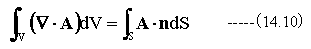
から求めることができます。（14.10）式の左辺は特異点を含むため計算できませんが、右辺は特異点を避けることができます。
従って、質量m1から流出するベクトル量の総和Smは
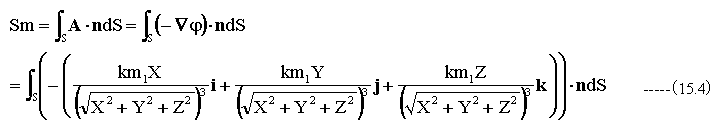
（15.4）式の計算を行うため、極座標に変換します。
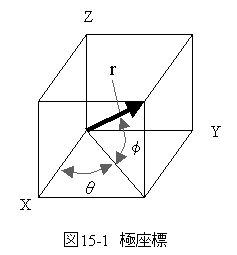図15-1に示す極座標において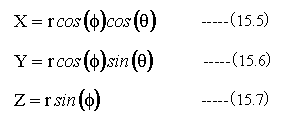
（15.5）式〜 （15.7）式式を用いて（15.4）式を変形すると
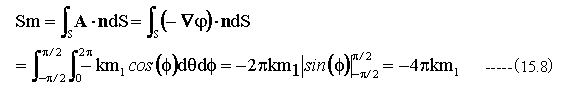
となります。（15.8）式の4πは球面の全立体角に一致します。
これから、質量m1から流出するベクトル量の総和は-4πkm1ということになります。
ちなみに2つの電荷QとQ’の間に生じる力は
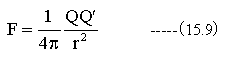
電荷Qによって生じる電界は
となって、重力場と類似の式となります。ここにも全立体角4πが定数として関係しています。
地球の重力場地上の重力加速度は9.8ｍ/ｓ＾2ですが、これがどのように生じるかをベクトル解析的に検討して見たいと思います。
重力加速度をベクトルAとします。また、単位体積あたりの質量をρとします。比例定数をｋとします。
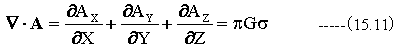
ここで重力加速度をベクトルAを
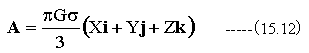
とすると
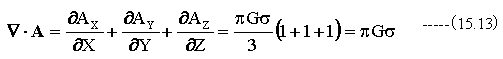
（が（15.11）式を満足することがわかります。
ここで地球を半径ｒの球体とすると質量ｍ1は
地上での重力加速度ベクトルAは距離ｒの2乗に反比例するので、球体を仮定すると下記の式が成立します。
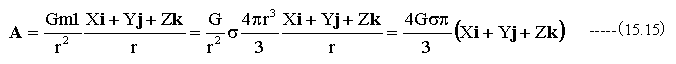
(15.15)式は（15.12）式に一致します。ベクトルの発散の式を使っても距離ｒの2乗に反比例の法則を使っても同じ結果が得られるということになります。
(15.15)式と（15.12）式は数学的テクニックの違いにすぎません。ただし (15.15)式と（15.12）式は球体を仮定した特殊解となっています。
地球の重力加速度の計算具体的に地球の重力加速度を計算してみましょう。 計算結果は下記表のようになります。
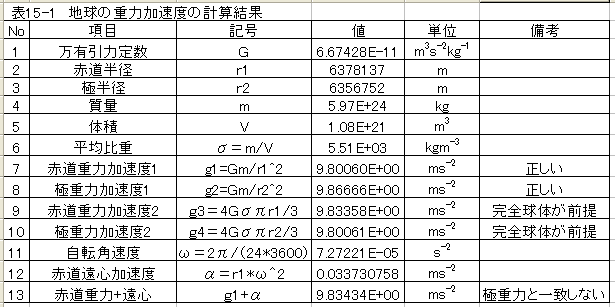
地球は完全な球体でなく、赤道半径と極半径が異なります。このため、完全球体を前提とした平均比重を用いた計算式では誤差が生じることがわかります。
単純に半径の２乗に反比例の式では、正確な値が求まります。赤道の方が極よりも重力加速度が小さくなります。
地球の赤道半径と極半径が異なる理由地球の赤道半径と極半径が異なる理由としては地球の自転による遠心力の影響が 考えられます。
具体的に遠心力の影響を計算した結果が表15-1のNo13です。この結果からすると 現在の自転速度では、赤道半径と極半径の差が小さくなるはずです。
太古の地球の誕生期には、現在よりも自転速度が速く、1日の時間が短かった のかもしれません？
ワークブック「ベクトル解析15.xls」のダウンロード表15-1のEXCELファイルは下記からダウンロードできます。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「ベクトル解析15.xls」をダウンロードする。
１６章：ベクトルの回転とストークスの定理に行く。