ベクトルの回転は、電磁気学でよく見かけられる数学記号です。ベクトルの回転の定義と意味を理解する必要があります。
ベクトルの回転の定義ベクトル関数をA(X,Y,Z)とするとき、ベクトルの回転は下記式で定義されます。
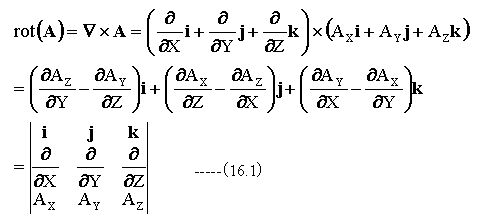
（16.1）式の等号は、全て同じ意味です。ベクトルの回転をrot(A)書く場合もあれば、▽×Aと書く場合もあります。
具体的な演算はベクトルの成分別に偏微分の差として計算されます。
ベクトルの回転の意味ベクトルの回転の意味を考える上でベクトルAを力のベクトルFに置き換えます。またrot(F)のｋ成分を考えます。
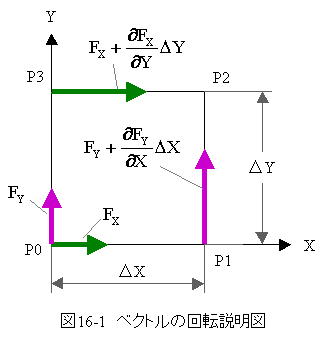
図16-1にベクトルの回転説明図を示します。
図16-1において、ΔX,ΔYの四角形P0,P1,P2,P3を考えます。
ここで、力Fと移動量の積の総和、すなわちエネルギーの総和をもとめます。
各辺のエネルギーは
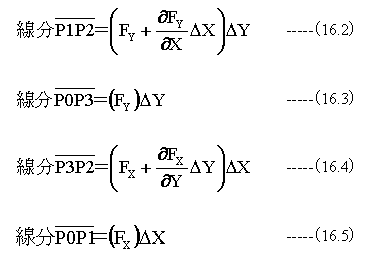
反時計方向を正にして各線分でのエネルギーの総和を求めると
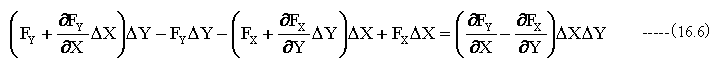
となって、ベクトルの回転の式と一致します。すなわちベクトルの回転を面で積分すると面の外周を一周した場合のエネルギーと一致します。
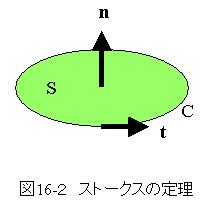
ストークスの定理図16-２にストークスの定理説明図を示します。
ベクトル関数をA(X,Y,Z)とするとき、閉曲線Cで囲まれた曲面Sとすれば下記式が成立します。
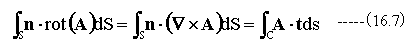
（16.7）式の右辺はベクトルAの回転と面の法線との内積の面積分です。
（16.7）式の左辺はベクトルAと接線との内積の線積分です。
ストークスの定理（16.7）式を成分別に展開すると以下のようになります。
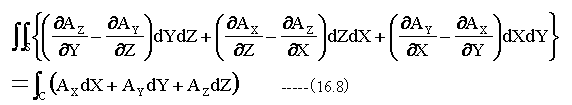
（16.8）式は、下記の（ベクトルの回転の意味での式）
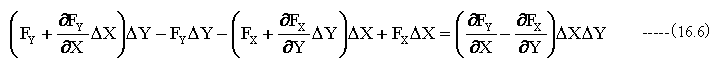
を一般化したものです。 （16.8）式の証明は省略しますが、ベクトル回転の面積分はベクトルの線積分に変換できます。またその逆も可能です。
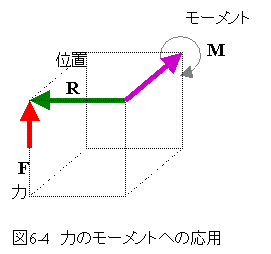
ベクトルの外積の回転図6-4に示す力のモーメントへの応用のように
の時
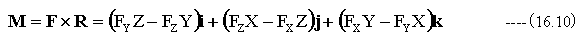
です。
Fx、Fy、Fzが定数の場合、ベクトルMの回転は
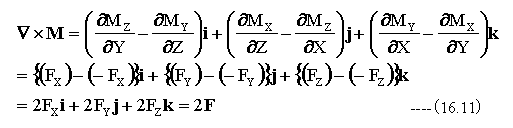
従って
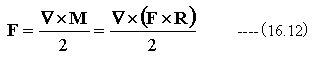
の関係が成立します。
１７章：涌点と吸点のある場での流れに行く。