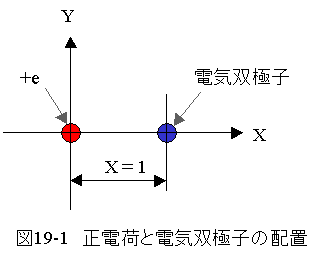
正電荷と電気双極子のある場正電荷と電気双極子のある場について考えてみたいと思います。
図1９-1における静電ポテンシャルは
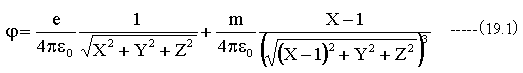
（19.1）式の３Dグラフを作成するにあたって、簡単化のため
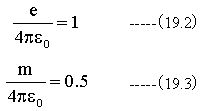
とします。
（19.1）式の計算結果を下記に示します。
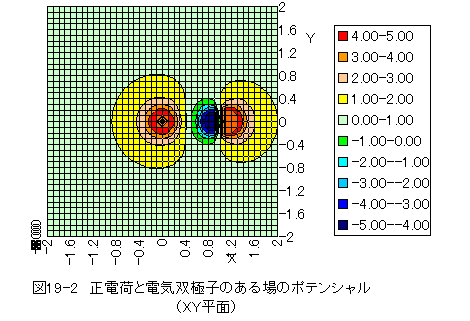
図19-2において、流れはポテンシャルの高い点から低い点に流れます。流れの方向はポテンシャルの等高面に垂直となります。
スカラーの勾配具体的にはスカラーの勾配であり、下記の式となります。
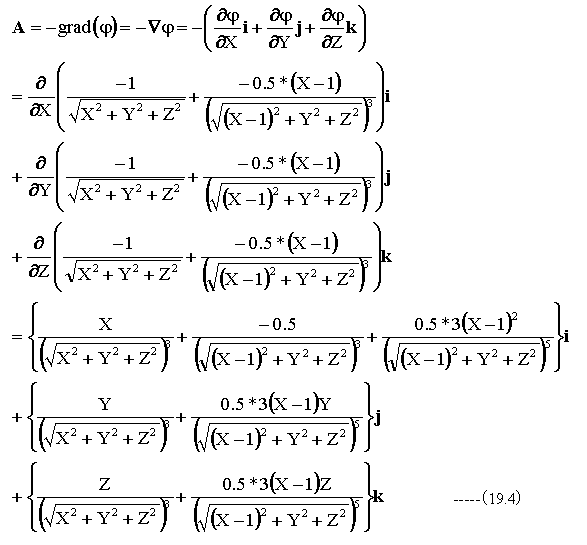
流線を描くにあたって、Z=0とします。 流線の方向はベクトルAの方向とします。 描く流線の長さをSとすると
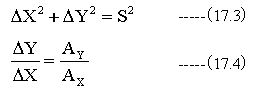
を満足するようにΔXとΔYを決定します。
従って
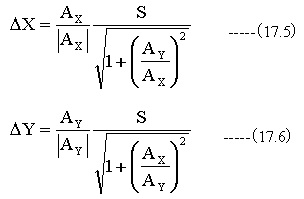
また、流線のスタートは涌点とし、角度Uを変数とします。
以上の条件で作図プログラムを作成します。
正電荷と電気双極子のある場演習EXCELを用いて、正電荷と電気双極子のある場演習を行い、正電荷と電気双極子のある場のイメージアップを図りましょう!!
ワークブック「ベクトル解析19.xls」のダウンロード下記のワークブック「ベクトル解析19.xls」（ベクトル作図プログラム）をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「ベクトル解析19.xls」をダウンロードする。ワークブック「ベクトル解析19.xls」説明- ワークブック「ベクトル解析19.xls」は複素関数機能を使用していません。
- 「ベクトル解析19.xls」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
- シート「操作」はパラメータの設定と操作を行います。
- シート「XY平面」はXY平面上の作図を行います。
- シート「ポテンシャル」はポテンシャルの３Dグラフを示します。
シート「操作」- X作図倍率 Mx：作図上のXの倍率を設定します。
- Y作図倍率 My：作図上のYの倍率を設定します。
- 角度間隔 dU(度)：作図上の角度間隔を設定します。
- 計算回数 N：角度の計算回数を設定します。
- 線分長さ dS：作図上の線分長さを設定します。
- 「作図実行」ボタンを押すと作図を実行します。
計算・作図結果入力条件を下記表に示します。
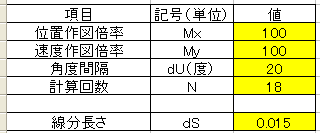
作図結果を下記に示します。
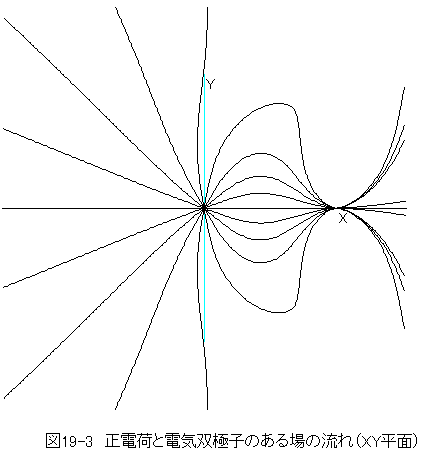
図19-3の0度の流れは吸点が無いため無限大に向かって流れます。
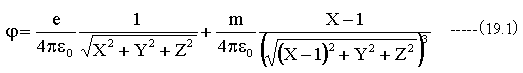
電束密度（19.1）式において、右辺の第1項は電荷によるポテンシャルであり、第2項は電気双極子によるポテンシャルです。
電束密度（でんそくみつど、electric flux density）は、電磁気学におけるベクトル場のひとつを表す物理量。国際単位系における単位は[C/m2]。電場と類似した概念であるが、誘電体を含む系において、電場の発散(div)を考える際には分極電荷の影響を加味しなければならないのに対し、電束密度の発散は真電荷のみによって定まるという違いがある。電気変位(electric displacement)とも呼ばれる。
電束密度D [C/m2] は、次のように定義される。
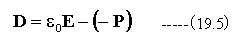
ここで、
ε0: 真空の誘電率 [F/m]
E: 電場 [V/m]
P : 分極 [C/m2]
具体的な正電荷による電束密度D [C/m2] は
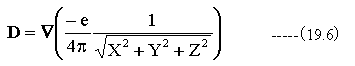
となり、（19.1）式の電気双極子の影響を除いた式となります。
ここで、分極Pは
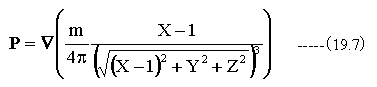
となります。分極Pの符号が反転していますが、ベクトルの方向の定義に関係していると思われます。
電束密度Dも分極Pもε0（真空の誘電率）が消えているのが特徴的です。
ここで、電束密度Dの発散を求めると
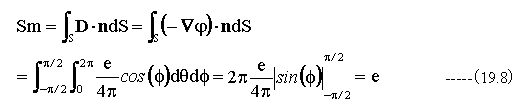
となり、特異点X=0における発散は電荷量eに一致します。また、特異点X=0以外での発散はゼロとなります。
以上のモデルでは、電荷は1点にあるとしましたが、空間的に分布した場合、電荷密度ρを用います。
電荷密度ρの空間の電束密度Dの発散は
（19.9）式はマクスウェルの方程式のひとつです。
また、物質の誘電率をεとした場合
ここで
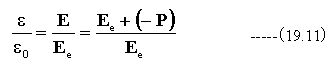
の関係があり、分極が大きいほど物質の誘電率εが大きくなることがわかります。
２０章：静磁場に行く。