静磁場の本質磁石は地球の南北を知る手段として古くから知られています。
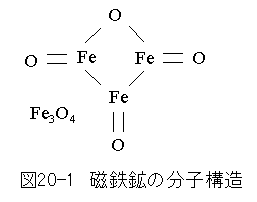
磁石の原料は自然界には図20-1に示す磁鉄鉱の形で存在します。
地球内部には酸化鉄が多く存在し、地球全体が磁石となり磁界を形成しているため、磁石を使って南北の方向を知ることができるのだと思います。
この磁力は、どのような仕組みで発生しているのか？厳密な説明はできませんが、電子のスピン（角運動）によって磁場が発生しているといわれています。
しかし、一般の物質は電子のスピン方向が正逆うまくバランスしており、磁場は発生しません。
酸化鉄のように特別の物質で電子のスピン方向のバランスが崩れ、磁場が発生するという説が一般的です。
磁石に対するクーロンの法則静磁場の本質は物理学で解明すべきです。ここでは、静磁場を数学モデルとしてどう扱うか？を検討したいと思います。
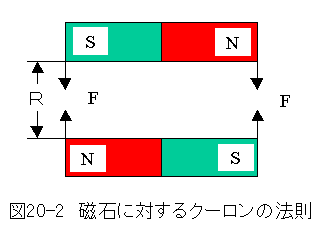
地球の北極にはS極があり、南極にはN極があります。磁石のN極は北極のS極に引かれ、磁石のS極は南極のN極に引かれます。従って、磁石のN極は北極の方向を指します。
クーロンはねじり天秤の実験によって、静電気の場合と同様に磁極の間に下記の力
が成立するのを確かめました。静電気の時と同様に（20.1）式を書き直すと
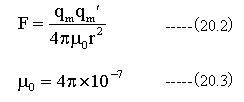
となります。
静磁場のポテンシャル磁石はN極とS極が必ず同じ大きさでペアーになり単独では存在しません。この性質は電気双極子と同じです。
電気双極子のポテンシャルは
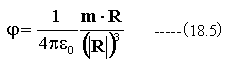
に対して、静磁場のポテンシャルは
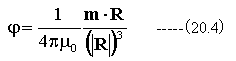
となります。 （20.4）式は磁気双極子のポテンシャルです。
磁場と磁束密度磁気においても、電気の場合と同様に磁気力の場を考えることができます。これを磁場といい、その強さをHで表します。
磁場Hはスカラーポテンシャルφの傾斜として求めることができます。
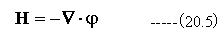
磁化ケイ素鋼のように、通常は磁力がなくても磁場中で磁石に変化する材料があります。これは通常は電子のスピン方向がランダムでトータルの磁気がゼロの状態から、磁場中で電子のスピン方向がそろってしまい、結果的に磁気を持つためといわれています。
このような現象を磁化といい、その大きさをMで表します。
磁束密度静電気において、電束密度Dを
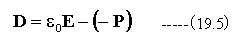
としました。同様に磁束密度Bを
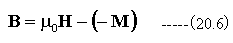
と定義できます。
また、静電気において、Dの発散は
でした。これに対して、磁気では「真磁荷」が存在しないことから
（20.7）式もマクスウェルの方程式のひとつです。
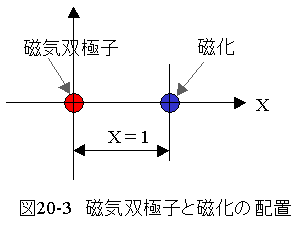
磁気双極子と磁化のある場磁気双極子と磁化のある場について考えてみたいと思います。
図20-3におけるポテンシャルは
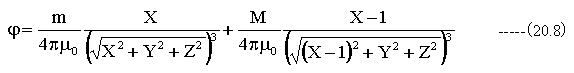
（20.8）式の３Dグラフを作成するにあたって、簡単化のため
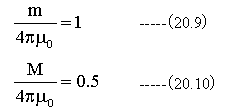
とします。
（20.8）式の計算結果を下記に示します。
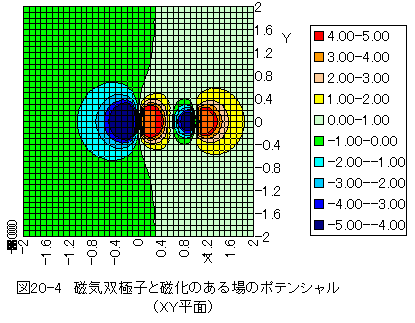
図20-4において、流れはポテンシャルの高い点から低い点に流れます。流れの方向はポテンシャルの等高面に垂直となります。
スカラーの勾配具体的にはスカラーの勾配であり、下記の式となります。
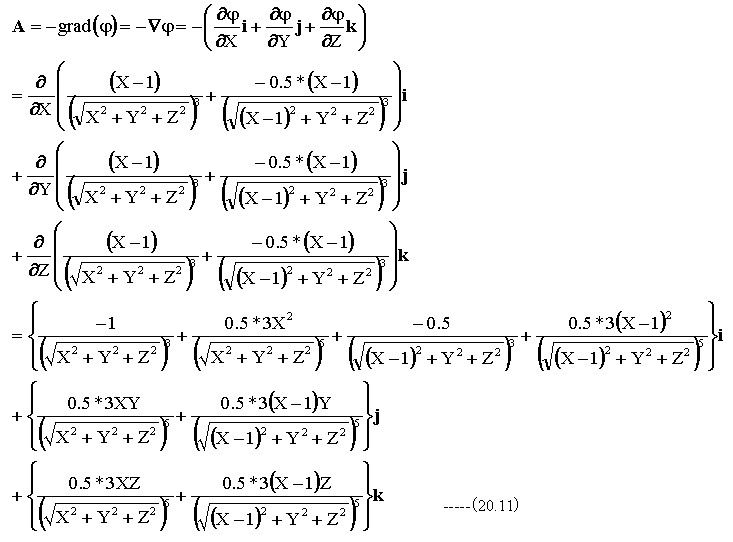
流線を描くにあたって、Z=0とします。
流線の方向はベクトルAの方向とします。
描く流線の長さをSとすると
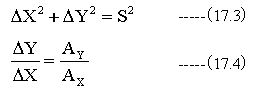
を満足するようにΔXとΔYを決定します。
従って
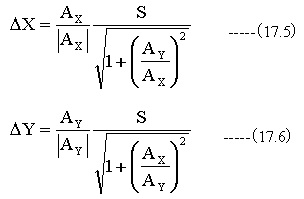
また、流線のスタートはX=-2とし、Yを変数とします。
以上の条件で作図プログラムを作成します。
磁気双極子と磁化のある場演習EXCELを用いて、磁気双極子と磁化のある場演習を行い、磁気双極子と磁化のある場のイメージアップを図りましょう!!
ワークブック「ベクトル解析20.xls」のダウンロード下記のワークブック「ベクトル解析20.xls」（ベクトル作図プログラム）をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「ベクトル解析20.xls」をダウンロードする。ワークブック「ベクトル解析20.xls」説明- ワークブック「ベクトル解析20.xls」は複素関数機能を使用していません。
- 「ベクトル解析20.xls」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
- シート「操作」はパラメータの設定と操作を行います。
- シート「XY平面」はXY平面上の作図を行います。
- シート「ポテンシャル」はポテンシャルの３Dグラフを示します。
シート「操作」- X作図倍率 Mx：作図上のXの倍率を設定します。
- Y作図倍率 My：作図上のYの倍率を設定します。
- Y間隔 dU：作図上のY間隔を設定します。
- 計算回数 N：Yの計算回数を設定します。
- 線分長さ dS：作図上の線分長さを設定します。
- 「作図実行」ボタンを押すと作図を実行します。
計算・作図結果入力条件を下記表に示します。
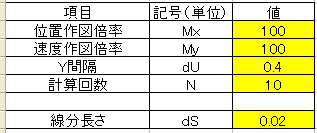
作図結果を下記に示します。
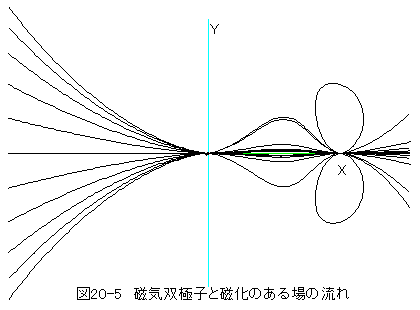
図20-5の流れは左から右に向かって流れます。
２１章：アンペアーの法則に行く。