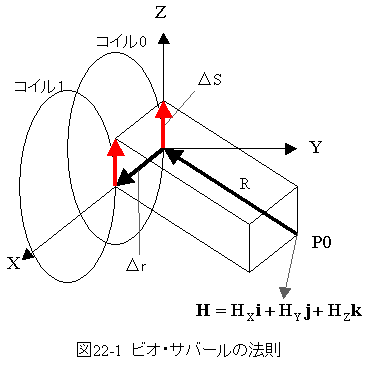
ビオ・サバールの法則アンペアーの法則では、コイルに流れる電流と磁位（ポテンシャル）の関係式が与えられたが、立体角で与えられるため、電流の微小部分による磁場への影響を知ることができません。
ビオ・サバールの法則は、この問題を解決します。
図22-1 ビオ・サバールの法則においてコイル0によるP0の磁場は
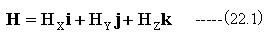
コイルをΔｒだけずらしたときP0点のポテンシャル変化Δφは
コイルをΔｒだけずらしたときP0点からの立体角の変化は スカラー3重積を用いて求めます。
Δｒ、 ΔS、Rの３重積は
スカラー3重積は３個のベクトルで作られた平行６面体の体積を与えます。これを長さ|R|で割れば、断面の面積が求まります。さらにこれを長さ|R|で割れば立体角が求まります。
従って、
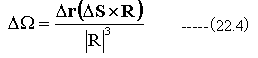
また、スカラー3重積は下記の関係が成立します。
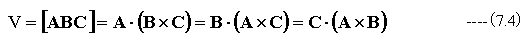
（22.2）式と（22.4）式から
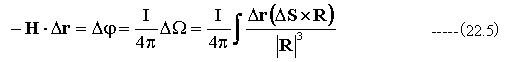
また
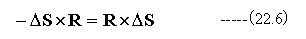
従って
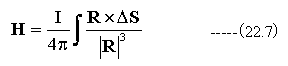
位置ベクトルRとΔSの成す角度をθとするならば
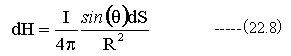
となり、電流の微小部分による磁場への影響を知ることができる。
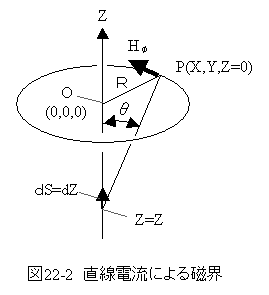
直線電流による磁界図22-2の直線電流による磁界に示す条件での磁界の強さを 求めます。
電流はZ軸にそって流れるとします。微小長さdS=dZとします。
Z=0で半径R上の磁界をHφとします。
（22.8）式から
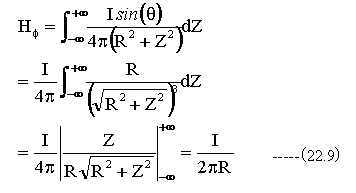
となります。
磁場の円周上積分磁場を円周上に1周積分するとどうなるであろうか？
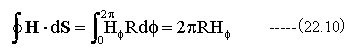
（22.9）式の結果を（22.10）式に代入すると
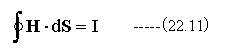
を得ます。
（22.10）式、 （22.11）式の結果は、一周して同一点に戻っても、積分値であるポテンシャルがゼロになりません。
この結果は、電流による磁場は一様連続なスカラーポテンシャルを持たないことを意味しています。これは、電流が流れる点で磁場が特異点となることを意味しています。
従って、電流による磁場はスカラーポテンシャルの勾配としての数学モデルが適用できないことを意味しています。
したがって、電流による磁場のグラフ表示はかなり厄介となります。
磁場の微分方程式電流が空間的に有限な密度を分布しているとき、下記式がどうゆう形をとるかを検討しましょう。
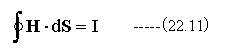
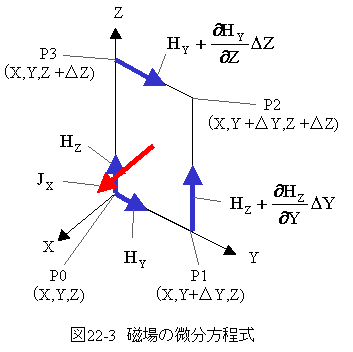
図22-3は電流密度JのX成分Jxと磁場の関係を示した図です。
図22-3おいて四角形P0,P1,P2,P3,P0の順に磁場の積分を行います。
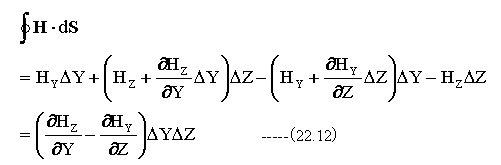
一方、X方向の電流Ixは
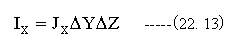
22.12)式と（22.13）式は等しくなければなりません。従って
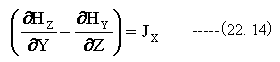
同様にして
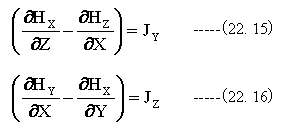
(22.14)式、(22.15)式、(22.16)式をベクトルの方程式で記載すると
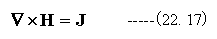
（22.17）式もマクスウェルの方程式のひとつです。
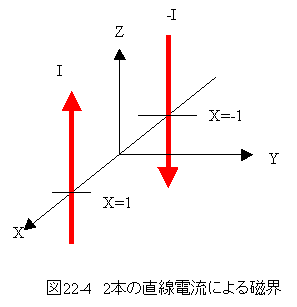
2本の直線電流による磁界図22-2の直線電流による磁界に示す条件での磁界の強さの 式（22.9）式から
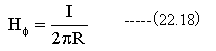
（22.18）式は円周方向の磁界を求める式であり、これを X,Y,Zの3次元ベクトルの式に変換すると
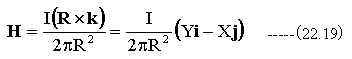
となります。XとY方向成分は
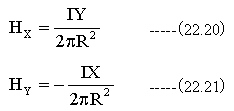
となります。図22-4に示す2本の直線電流による磁界は下記式となります。
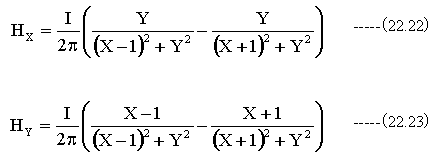
となります。磁界の強さは
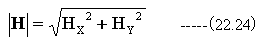
となります。
2本の直線電流による磁界の作図作図は簡単化のため下記条件とします。
（１）図22-5に2本の直線電流による磁界Hxを示します。
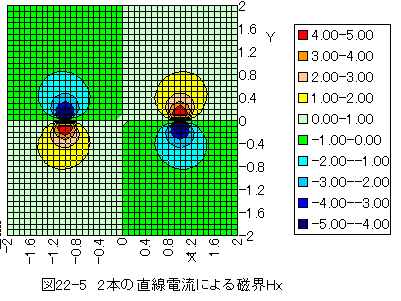
（１）図22-6に2本の直線電流による磁界Hｙを示します。
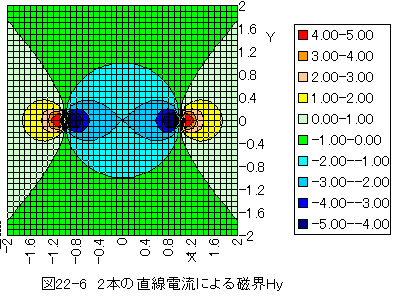
（１）図22-7に2本の直線電流による磁界|H|を示します。
図22-5、図22-6、図22-7に示すように、電流による磁界はスカラーポテンシャル で表示できません。
電流による磁界は大きさと方向を持ったベクトルです。全ての値を同時にグラフ化 できません。
X,Y,Z成分ごとのグラフと絶対値（大きさ）のグラフに分割して表示するきりありません。
方向については、X,Y,Z成分ごとのグラフから推定する必要があります。
図22-7から、2本の直線電流による磁界の領域は長円形になり、電流の近傍が 強くなることがわかります。
ワークブック「ベクトル解析22.xls」のダウンロードグラフのEXCELファイルは下記からダウンロードできます。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「ベクトル解析22.xls」をダウンロードする。
２３章：ベクトルポテンシャルに行く。