ファラデーの誘導則電流と電流は互いに力を及ぼしあい、また電流と磁石との間にも力が作用する。
この逆の現象、すなわち電流と運動、または磁石と運動から電流を生ずる現象がないか？ということをファラデーが予測して実験を行った。
電磁誘導それ自身を見出したのはファラデーである。（1831年）
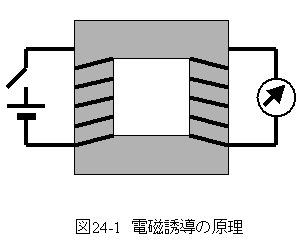
図24-1に示すような回路において、一方に電流を定常的に流しても、もう一方の回路に電流は流れない。
しかし、スイッチを入れた時と切る時にもう一方の回路に電流が流れる。
スイッチを入れた時と切る時は電流計が逆に振れる。
この実験結果から得られた結論をノイマンは次の様に言い表した。
ある回路に誘起される起電力(Em)はその回路を貫く磁束（Φ）が減少する速度の比例する。すなわち
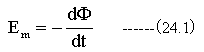
磁気抵抗図24-1に示すトランスの磁気抵抗を求めてみましょう。
電流と磁場の関係式は巻き数をnとすると
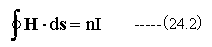
磁束密度と磁場の関係は
鉄心断面についてのBn（断面の法線方向成分）の面積積分（S)が磁束（Φ）です。
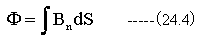
ここで、磁気抵抗Rmを下記ように定義します。
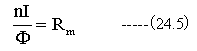
図24-1に示すトランスにおいて、透磁率μの鉄心で作った磁気回路で内部が一様な磁場Hが存在するならば、鉄心の一周の長さをLとして
となる。これを（24.5）式に代入すると
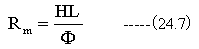
を得る。鉄心の断面積をSとすると、断面に磁束密度μHが通っているから、磁束Φは
(24.7)式に（24.8）式を代入して
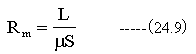
が得られる。磁気抵抗Rmは鉄心の透磁率μと断面積Sと一周の長さLのみで決定されることがわかる。 磁気抵抗Rmが既知の場合、磁束（Φ）は
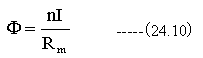
となります。
地磁気での発電電磁誘導は、モータ、発電機、変圧器等さまざま応用されています。
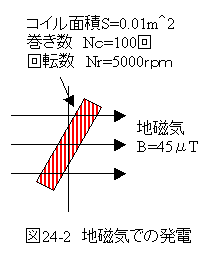
一例として、地磁気の測定について検討してみたいとおもいます。
図23-2の地磁気での発電における起電力は
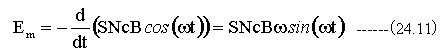
となります。実際に計算すると図24-3のグラフに示すように なります。
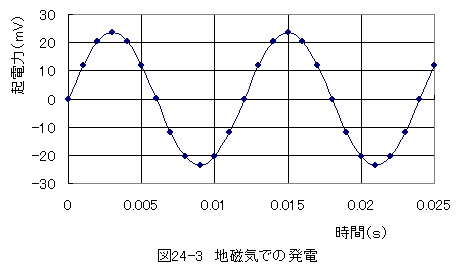
実際には外乱ノイズがありますので、十分な外乱ノイズ対策を行えば、このような方法で地磁気の測定が可能と思われます。
ファラデーの誘導則の諸形式磁場Hの中で導線が速度Vで動くとき、導線には起電力を生じ、もし導線が一つの閉回路を作っていれば、電流が流れる。
この時の起電力Emは、回路を貫く磁束の時間的変化に等しい。すなわち
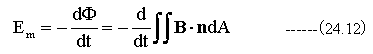
ここで、Aはコイルのふちを含む曲面であり、B・ｎそれに垂直な磁束成分である。
ところが、コイルの要素dSが速度Vで動く場合には、dSが通った面積を貫く磁束の量はdtの時間において下記となります。
従って
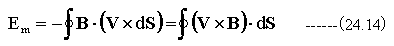
となります。
マクスウェルの方程式また、コイルの起電力Emははコイルの道筋に沿って電場を線積分することによっても得ることができます。
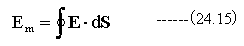
（24.12）式と（24.15）式から
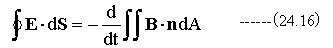
（24.16）式の左辺にストークスの定理を適用すると
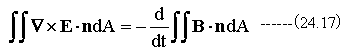
（24.17）式を変形すると
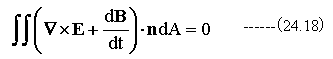
従って
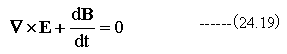
となります。
（24.19）式はマクスウェルの方程式の内の一つです。
２５章：マクスウェルの方程式に行く。