これまでに導いた式これまでに導いた式は以下の通りです。
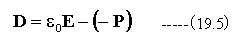
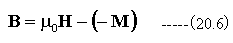
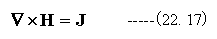
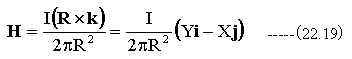
上記の式の中で（22.17）式は一つの矛盾を含んでいます。
（22.17）式の補正電流密度Jの発散は
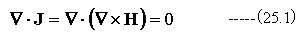
となり、発散はゼロとなります。これは定常状態では成立しますが、過渡応答時は場所により電荷密度の変化が生じるため、発散はゼロとなりません。
過渡応答時の電荷密度の変化の影響を下記のように補正する必要があります。
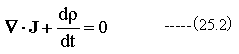
ここで、（19.9）式を微分すると
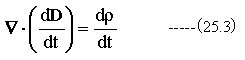
（25.2）式と（25.3）式から
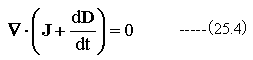
となります。ここで（22.17）式の電流密度Jを下記式で置き換えます。
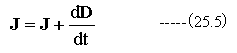
すなわち
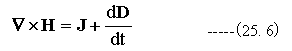
マクスウェルの方程式まとめ（25. 6）式を用いて整理すると
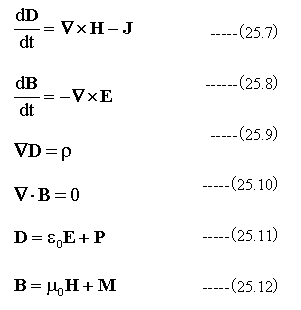
となります。（25.7）式から（25.12）式が整理されたマクスウェルの方程式です。
マクスウェルの方程式とは、電磁気の相互作用を微分形式で纏めた方程式です。微分方程式の性格上この方程式を満足する解は無限に在ります。
従って、この方程式から具体的な数学モデルを特定することはできません。
しかし、特定条件の電磁気を表現した数学モデルは、マクスウェルの方程式を満足する必要があります。
２６章：マクスウェルの方程式と電磁波に行く。