マクスウェルの基本方程式電磁波は電場Eと磁場Hの振動として、空間を伝播します。電場と磁場の関係を数式で記述した式がマックスウェルの方程式です。従って、電磁波の基礎式はマックスウェルの方程式から導びかれます。
マクスウェルの方程式は電場E、磁場H、電気変位D、磁気誘導B、電流密度Jの関係をベクトルの方程式で表しております。
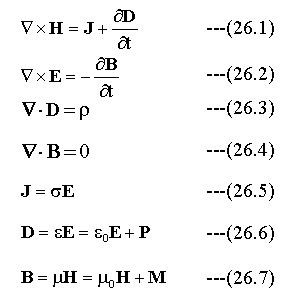
ρは電荷密度、σは導電率、εは物質の誘電率、ε0は真空の誘電率で8.854×10-12F・m-1、μは物質の透磁率、μ0は真空の透磁率で1.257 ×10-12H・m-1です。また、Pは原子・分子の電荷分布が変化して生じる分極、Mは磁化分布が変化して生じる磁化です。
（22.17）マクスウェルの基本方程式の変形波動の伝播を扱う場合、物質中の電荷密度ρを0として扱います。また、ほとんどの物質で高い周波数に磁化Mは追従できないためM=0とします。この条件でマクスウェルの方程式を変形します。
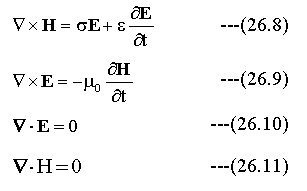
ベクトル解析の公式
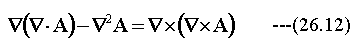
を(26.9)式に適用します。
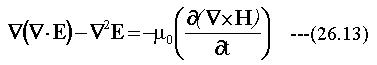
(26.13)式に(26.8)(26.10)式を代入して整理します。
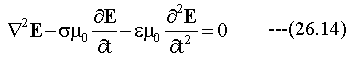
同様に、磁場Hについても下記の波動方程式を得ます。
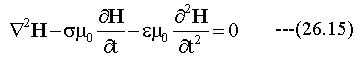
波動方程式はEとHのx,y,z方向の各成分で独立に成り立ちますが、それぞれの成分をスカラー関数V(r,t)で代表させて下記のスカラー波動方程式を得ます。
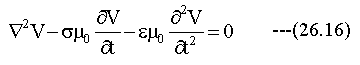
ヘルムホルツの方程式(26.16)式はスカラー関数V(r,t)の偏微分方程式の形となっています。この解として下記の調和振動波式を代入します。
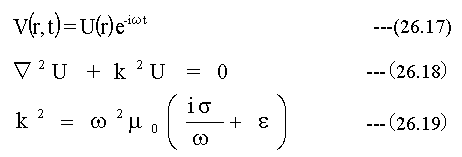
(26.18)式を偏微分の形式で表すと
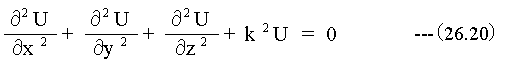
となります。このように、調和振動する波を考えると波動方程式を位置rのみに関する微分方程式に帰着できます。この式を解くことで波動の空間的な伝播特性を知ることができます。
誘電体中での波動方程式導電率σが0の場合、電磁波の電場よる電流の発生がなく、電磁波のエネルギー損失が発生しません。このため電磁波のエネルギーは失われず物質は透明となります。ガラス、空気、真空などの場合で、この様な物質を誘電体または絶縁体といいます。
この場合の波動方程式は下記のように単純化できます。
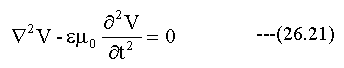
（26.21）式をｘ方向の1次元の式に置き換えます。
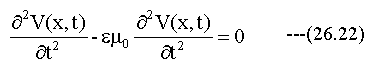
(26.22)式を満足する解として
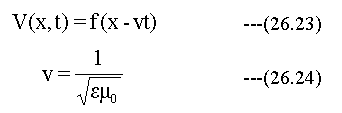
(26.23)式は下記の図26.1に示すように速度vで波が伝播することを示しています。
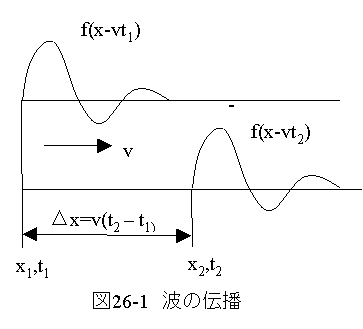
真空中の光速度Cはε0を真空中の誘電率として
誘電体の屈折率nは
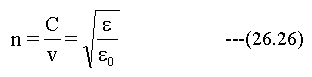
誘電体中の波数kは（26.19） 式のσ＝0として
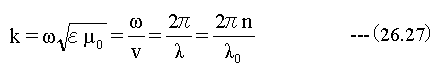
の関係が成立します。
導体中での波動方程式ヘルムホルツの方程式（26.18） （26.19）式をｘ方向の1次元の式に置き換えます。
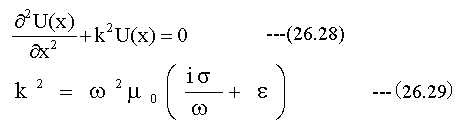
(26.28)式を満足する解として
を得ます。ここで導体中ではσ≠0であり波数ｋは複素数となります。
(26.31)式を(26.30)式に代入します。
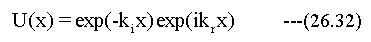
波数kの虚数部kiは減衰項として作用することがわかります。
同様に導体中の屈折率も真空中の波長をλ0として下記のように定義できます。
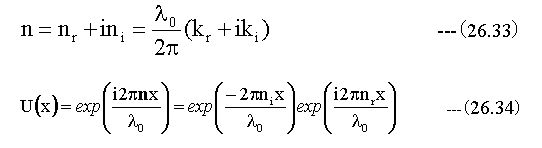
複素屈折率の虚数部は電磁波の減衰として作用します。
電場と磁場の関係電磁波は電場（電界）と磁場（磁界）の振動が伝搬（伝わる）する現象のことです． 真空中を伝わる電磁波は，光速ｃで伝搬し， 電場と磁場の振動方向は互いに垂直でかつ進行方向に垂直です． ふつう，電場はベクトルEで，磁場はベクトルHで表現されます。
ここで，電磁波の進行方向と磁場Hを含む面を電磁波の偏りの面又は「偏光面」，また． 電場Eを含む面を「振動面」といいます． また， 偏光面の方向が揃っている場合を「偏光」といいます。
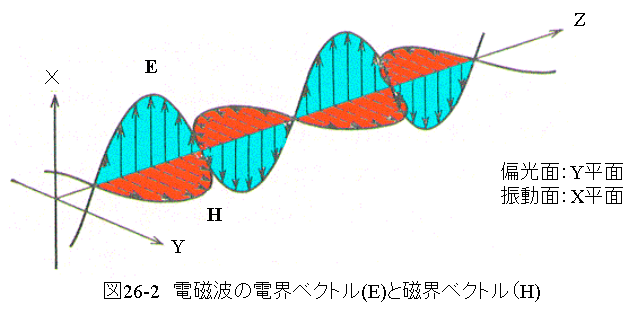
図26-2に示す電磁波を式で表すと下記のようになります。
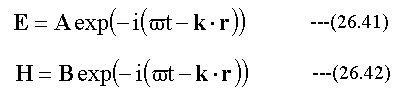
(26.41)(26.42)式においてAとBはベクトルの定数です。またωは角速度、ｋは波数ベクトル、ｒは位置ベクトルです。
波数ベクトルｋは（26.26） または（26.29）式のｋに電磁波の進行方向単位ベクトルをかけたものです。図26-2の条件においては単純に
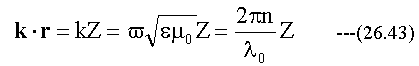
となります。 (26.41)(26.42)式を(26.9)式に代入します。
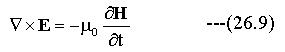
まず、(26.9)式の左辺を計算します。▽×Eはベクトルの回転と呼ばれる計算式であり、下記のように行列式で展開できます。
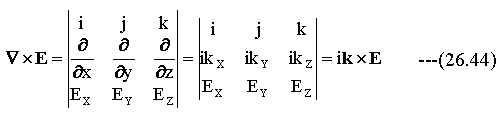
(26.9)式の右辺は
(26.44)と(26.45)式から
同様にして
の関係式が得られます。(26.46) (26.47)式は電磁波の進行方向を表す波数ベクトル(ｋ) と電界ベクトル(E)と磁界ベクトル（H)がベクトルの外積の形で与えられ、お互いに垂直であることを表しています。
２７章：ベクトル解析の公式まとめに行く。