ベクトルの微分ベクトルも実数と同様に微分が可能です。
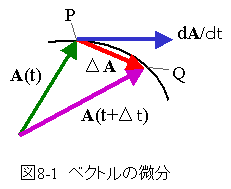
ベクトルＡをスカラー変数ｔに一価連続関数として微分の説明図を図8-1に示します。
ｔにおけるベクトルＡをＡ（ｔ）とします。これをＰ点とします。t+ΔｔにおけるベクトルＡをＡ（ｔ+Δｔ）とします。これをＱ点とします。
また、ΔＡ＝Ａ（ｔ+Δｔ）-Ａ（ｔ）です。
ベクトルＡの微分は下記式で定義できます。
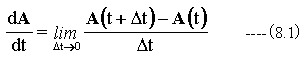
図8-1に示すように、dA/dtは曲線の接線となります。
ベクトルAを基本ベクトルに分解して表示すると下記のようになります。
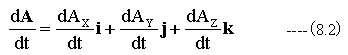
（8.2）式において、Ax、Ay、Azはスカラー変数であり、実数の微分がそのまま適用できることがわかります。
単位接線ベクトル図8-1においてΔAの絶対値Δｓは下記式となります。
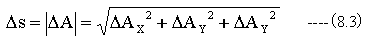
ベクトルAをΔSで微分すると
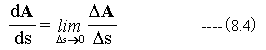
となり、ｄA/ｄsは絶対値が1の単位接線ベクトルとなります。
高次の微分ベクトルAの高次の微分も全く同様行うことができます。
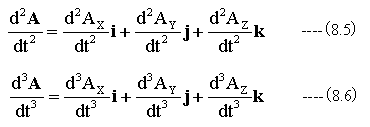
ベクトルの微分公式ベクトルの微分法については、ベクトルを基本ベクトルに分解し、ijkの方向別のスカラー変数に分解するならば、実数の微分公式が適用できます。
分解しない場合の微分公式を下記に示します。
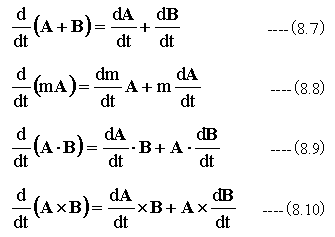
（8.7）式の証明下記式の展開から明らかです。
（8.8）式の証明下記のように式を展開します。
（8.9）式の証明下記のように式を展開します。
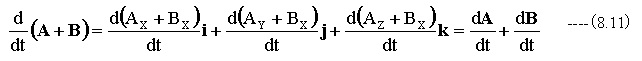
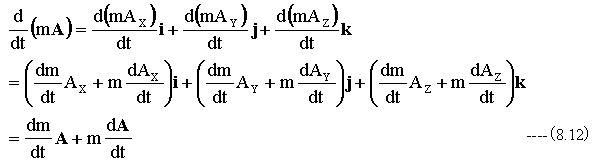
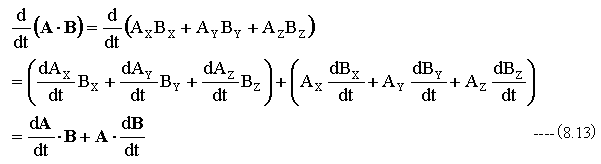
（8.10）式の証明下記のように式を展開します。
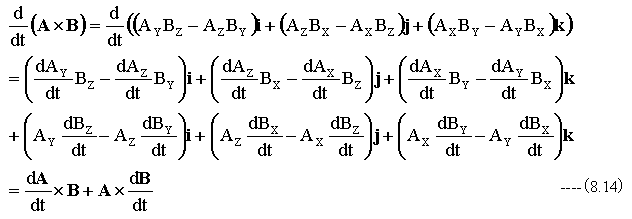
ベクトルの具体的な演算は一般的に基本ベクトルijkの成分に分割し、スカラー変数にして行う必要があります。この場合、実数の公式は適用できますので、ベクトルの微分公式使わなくても微分は可能です。
ベクトルの不定積分ベクトルも実数と同様に不定積分ができます。
もし、下記式が成立する場合
下記の不定積分が成立します。
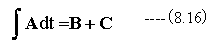
（8.16）式において、Cはｔに無関係な定ベクトルです。
ベクトルのベクトルの定積分ベクトルも実数と同様に定積分ができます。
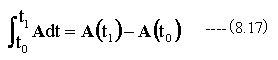
空気抵抗が無い場合の放射物体の運動重力の加速度をg、重力の方向をZ軸に-kとすれば、放射体のいちベクトルをｒとすれば、
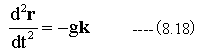
積分して
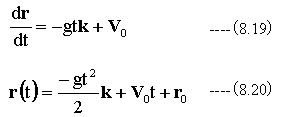
（8.20）式において、V0はｔ＝0の速度ベクトル、ｒ0はｔ＝0における位置ベクトルです。
（8.20）式をXYZ成分に分解すると
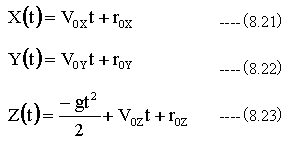
となります。実際の計算はXYZ成分に分解して行います。
空気抵抗が無い場合の放射物体の運動演習EXCELを用いて、空気抵抗が無い場合の放射物体の運動演習を行い、空気抵抗が無い場合の放射物体の運動のイメージアップを図りましょう!!
ワークブック「ベクトル解析8.xls」のダウンロード下記のワークブック「ベクトル解析8.xls」（ベクトル作図プログラム）をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「ベクトル解析8.xls」をダウンロードする。ワークブック「ベクトル解析8.xls」説明- ワークブック「ベクトル解析8.xls」は複素関数機能を使用していません。
- 「ベクトル解析8.xls」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
- シート「操作」はパラメータの設定と操作を行います。
- シート「XY平面」はXY平面上の作図を行います。
- シート「YZ平面」はYZ平面上の作図を行います。
- シート「数値」は計算結果の数値データです。
シート「操作」- 位置作図倍率 Mr：作図上の位置の倍率を設定します。
- 速度作図倍率 Mv：作図上の速度の倍率を設定します。
- 時間間隔 dt(s)：計算時間間隔を設定します。
- 計算回数 N：計算回数を設定します。
- 重力加速度 ｇ(m/s^2)：重力加速度を設定します。
- 初期速度 V0(m/s)：初期速度のXYZ成分を設定します。
- 初期位置 ｒ0(m)：初期位置のXYZ成分を設定します。
- 「作図実行」ボタンを押すと作図を実行します。
計算・作図結果入力条件を下記表に示します。
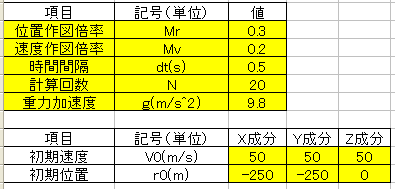
作図結果を下記に示します。
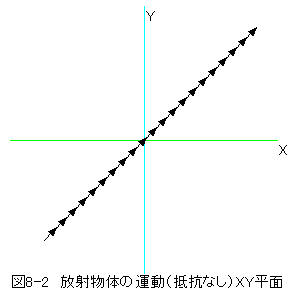
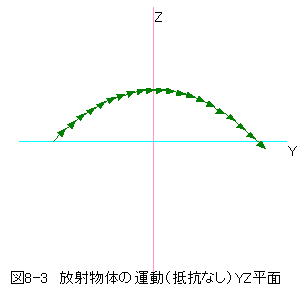
図8-2と図8-3において、ベクトルの始点はXYZの位置座標、ベクトルの方向と長さが速度 ベクトルで表示しています。
９章：空気抵抗がある場合の放射物体の運動に行く。