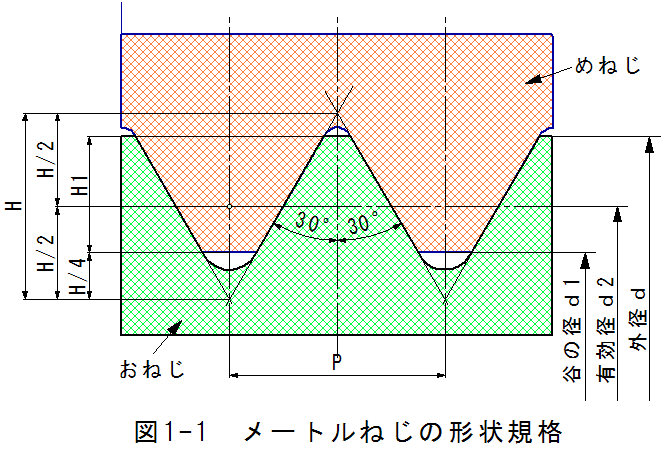
メートルねじの形状規格図1-1にメートルねじの形状規格図を示します。
図1-1において
H=0.866025×P ----（1.1）式
H1=0.541266×P ----（1.2）式
d1=d-1.082532×P ----（1.3）式
d2=d-0.649519×P ----（1.4）式
の関係式で規定されています。
従ってメートルねじは、ねじ外形dとピッチPが決定されると、 ねじの形状が全て計算で求まることになります。
上記の関係式はメートル並目ねじ、細目ねじ共通に成立します。
メートルねじの寸法と標準締付けトルクメートルねじの寸法と標準締付けトルクを以下の表に示します。
| ねじの呼び | ピッチP | 外径d | "谷の径 d1=d-0.649519*P" | "有効径 d2=d-1.082532*P" | 標準締め付けトルク（N・m） |
| M2 | 0.4 | 2 | 1.567 | 1.740 | 0.176 |
| M2.5 | 0.45 | 2.5 | 2.013 | 2.208 | 0.36 |
| M3 | 0.5 | 3 | 2.459 | 2.675 | 0.63 |
| M4 | 0.7 | 4 | 3.242 | 3.545 | 1.5 |
| M5 | 0.8 | 5 | 4.134 | 4.480 | 3 |
| M6 | 1 | 6 | 4.917 | 5.350 | 5.2 |
| M8 | 1.25 | 8 | 6.647 | 7.188 | 12.5 |
| M10 | 1.5 | 10 | 8.376 | 9.026 | 24.5 |
| M12 | 1.75 | 12 | 10.106 | 10.863 | 42 |
| M16 | 2 | 16 | 13.835 | 14.701 | 106 |
| M20 | 2.5 | 20 | 17.294 | 18.376 | 204 |
| M24 | 3 | 24 | 20.752 | 22.051 | 360 |
| M30 | 3.5 | 30 | 26.211 | 27.727 | 700 |
| M36 | 4 | 36 | 31.670 | 33.402 | 1240 |
| M42 | 4.5 | 42 | 37.129 | 39.077 | 2000 |
推力・応力・歪計算に必要なSUS304の物性メートルねじを標準締付けトルクで締付けた場合の推力・応力・歪を計算するために 必要な物性を以下の表に示します。
| 項目 | 値 | 単位 |
| 摩擦係数 | 0.5〜0.6 | 無次元 |
| 縦弾性係数 | 193000 | N/mm2 |
| 耐力 | 206 | N/mm2 |
| 引張強度 | 520 | N/mm2 |
上記の表において、摩擦係数は推力計算に大きく影響する物性ですが、一般的に 不安定であり、大きなバラツキが生じます。ここでは、摩擦係数=0.55として計算することに します。
縦弾性係数は、発生する応力による歪量を計算するとき必要となる物性です。
耐力とは、弾性変形が限界に達する応力の値です。 耐力を越える応力がかかった 場合、SUS304は永久変形が残ります。
引張強度とは完全に破壊する応力の値です。
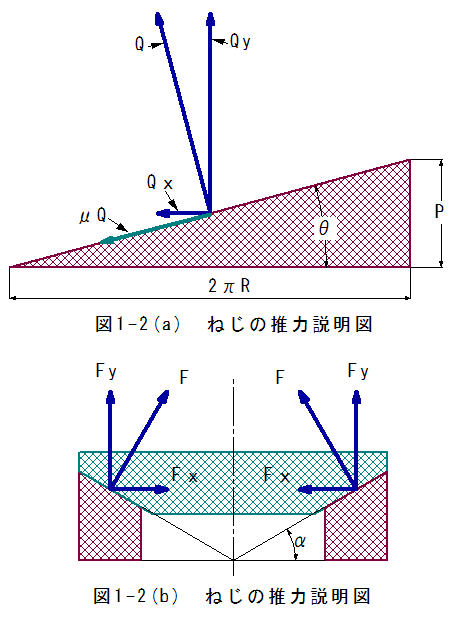
推力の計算式図1-2(a)にねじを有効径ｄ2で円周方向に展開した図を示します。
図1-2(a)において、
P＝ねじピッチ
R＝ねじ有効半径＝ｄ2/2
θ＝斜面の角度
Qy＝Y方向の力（軸方向）
Qx＝X方向の力（円周方向）
Q=斜面と直角方向の力
μ＝摩擦係数
です。
図1-2(a)から下記の関係式が成立します。
Q＝Qy/COS（θ） ---（1.1）式
Qによる摩擦力Gは斜面の方向に下記式の大きさとなります。
G=μQ ---（1.2）式
摩擦力GのX方向成分Gxは
Gx＝G・COS（θ） ---（1.3）式
X方向（円周方向）合計の力Hｘは
Hｘ＝Qx+Gx ---（1.4）式
（1.4）式に（1.3）式、（1.2）式、（1.1）式を代入して整理すると
Hｘ＝Qｙ（P/（2πR) + μ） ---（1.5）式
となります。
ここで、トルクTは
T=Hｘ・R ---（1.6）式
の関係があります。
（1.5）式に（1.6）式を代入すると
T＝Qｙ（P/（2π) + μR） ---（1.7）式
となります。
（1.7）式は、矩形ねじの場合は成立するのですが、図1-1に示すメートルねじの断面形状には 適用できません。
ねじの断面形状の影響を補正する必要があります。
図1-2(b)にこの説明図を示します。
図1-2(b)のαはねじ断面の角度です。メートルねじの場合α＝30°となります。
図1-2(a)のQの力が図1-2(b)のFｙに対応します。 これは、図1-2(a)が円周方向成分を示しているのに対して、図1-2(b)は半径方向成分を示している ためです。ねじの斜面は立体斜めになっているのです。
摩擦力は、立体斜めのねじの斜面と垂直の力に摩擦係数を掛けた値となります。
立体斜めを考慮した摩擦力Gは
G=μQ/COS(α） ---（1.8）式
摩擦力GのX方向成分Gxは
Gx＝μQCOS（θ）/COS(α） ---（1.9）式
となります。
従って、トルクTは
T＝Qｙ（P/（2π) + μR/COS(α）） ---（1.10）式
となります。
（1.10）式を変形して推力Qｙ
Qｙ＝T/（P/（2π) + μR/COS(α）） ---（1.11）式
（1.10）式はねじを締めるときに必要なトルクの式です。 ねじを緩めるときは、摩擦力は逆方向に働きます。従って、
Tb＝Qｙ（P/（2π) - μR/COS(α）） ---（1.12）式
となります。
ねじの推力と緩める場合のトルク計算結果ねじの推力と緩める場合のトルク計算結果を下記の表に示します。
計算条件
・摩擦係数 μ＝0.55
・ねじ断面の角度 α＝30°
| ねじの呼び | ピッチP | 外径d | "有効半径 R" | 標準締め付けトルク（N・m） | "推力 N" | 緩めるトルク（N・mm） |
| M2 | 0.4 | 2 | 0.870 | 0.176 | 286 | -140 |
| M2.5 | 0.45 | 2.5 | 1.104 | 0.360 | 466 | -293 |
| M3 | 0.5 | 3 | 1.338 | 0.630 | 678 | -522 |
| M4 | 0.7 | 4 | 1.773 | 1.500 | 1212 | -1230 |
| M5 | 0.8 | 5 | 2.240 | 3.000 | 1935 | -2507 |
| M6 | 1 | 6 | 2.675 | 5.200 | 2798 | -4309 |
| M8 | 1.25 | 8 | 3.594 | 12.500 | 5037 | -10496 |
| M10 | 1.5 | 10 | 4.513 | 24.500 | 7891 | -20732 |
| M12 | 1.75 | 12 | 5.432 | 42.000 | 11266 | -35724 |
| M16 | 2 | 16 | 7.350 | 106.000 | 21257 | -92467 |
| M20 | 2.5 | 20 | 9.188 | 204.000 | 32728 | -177956 |
| M24 | 3 | 24 | 11.026 | 360.000 | 48130 | -314039 |
| M30 | 3.5 | 30 | 13.863 | 700.000 | 74775 | -616695 |
| M36 | 4 | 36 | 16.701 | 1240.000 | 110289 | -1099575 |
| M42 | 4.5 | 42 | 19.539 | 2000.000 | 152383 | -1781728 |
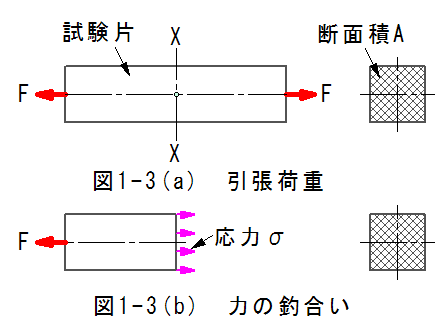
応力の計算図1-3(a)に試験片に引張荷重Fをかけた状態の図をしめします。
試験片の断面積はAとします。
ここで、任意の断面XXの左側の力の釣合いを考えます。
力の釣合いを図1-3(b)に示します。
断面XXには均一に分布した力が発生し、これを応力（σ）と呼びます。
応力（σ）は単位面積あたりの力で定義されます。 力の釣合いから
σA＝F ---（1.13）式
が成立します。（1.13）式から応力（σ）は
σ＝F/A ---（1.14）式
となります。
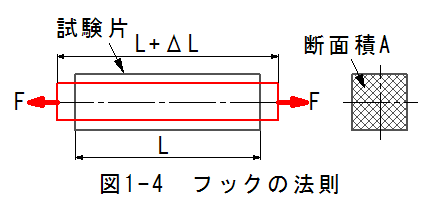
歪の計算図1-4にフックの法則の説明図を示します。
図1-4において、黒は引張荷重Fをかける前、赤は引張荷重Fをかけた 状態を示します。
ここで長さLの変化量ΔLは、比例定数をCとして 下記の関係式が成立します。
ΔL＝CFL/A ---（1.15）式
（1.15）式に（1.14）式を代入すると
ΔL＝CLσ ---（1.16）式
となります。
ここで歪εは下記のように定義されます。
ε＝ΔL/L ---（1.17）式
（1.16）式と（1.17）式式から
ε＝Cσ ---（1.18）式
が得られます。
ここで、縦弾性係数Eは下記のように定義されています。
E=1/C ---（1.19）式
（1.18）式に（1.19）式を代入して
ε＝σ/E ---（1.20）式
が得られます。 これをフックの法則と呼びます。
長さLの変化量ΔLは
ΔL＝εL ---（1.21）式
として求めることができます。
長さL、ピッチPのメートルねじの締め上げ回転角度βは
β＝360×ΔL/P ---（1.22）式（単位 °）
として求めることができます。
応力と歪の計算結果応力と歪の計算結果を下記の表に示します。
計算条件
・摩擦係数 μ＝0.55
・ねじ断面の角度 α＝30°
・縦弾性係数 E=193000 （N/mm2）
・面積計算は谷の半径を使用
・ねじの有効長さ L=100mm
| ねじの呼び | ピッチP | 外径d | "谷の半径 R" | 標準締め付けトルク（N・m） | "推力 N" | "応力 σ" | 歪 | "100mm 当たりの伸び" | "回転角度 （度）" |
| M2 | 0.4 | 2 | 0.7834936 | 0.176 | 286 | 148 | 0.000767 | 0.0767 | 69.1 |
| M2.5 | 0.45 | 2.5 | 1.0064303 | 0.36 | 466 | 146 | 0.000759 | 0.0759 | 60.7 |
| M3 | 0.5 | 3 | 1.229367 | 0.63 | 678 | 143 | 0.000740 | 0.0740 | 53.3 |
| M4 | 0.7 | 4 | 1.6211138 | 1.5 | 1212 | 147 | 0.000761 | 0.0761 | 39.1 |
| M5 | 0.8 | 5 | 2.0669872 | 3 | 1935 | 144 | 0.000747 | 0.0747 | 33.6 |
| M6 | 1 | 6 | 2.458734 | 5.2 | 2798 | 147 | 0.000763 | 0.0763 | 27.5 |
| M8 | 1.25 | 8 | 3.3234175 | 12.5 | 5037 | 145 | 0.000752 | 0.0752 | 21.7 |
| M10 | 1.5 | 10 | 4.188101 | 24.5 | 7891 | 143 | 0.000742 | 0.0742 | 17.8 |
| M12 | 1.75 | 12 | 5.0527845 | 42 | 11266 | 140 | 0.000728 | 0.0728 | 15.0 |
| M16 | 2 | 16 | 6.917468 | 106 | 21257 | 141 | 0.000733 | 0.0733 | 13.2 |
| M20 | 2.5 | 20 | 8.646835 | 204 | 32728 | 139 | 0.000722 | 0.0722 | 10.4 |
| M24 | 3 | 24 | 10.376202 | 360 | 48130 | 142 | 0.000737 | 0.0737 | 8.8 |
| M30 | 3.5 | 30 | 13.105569 | 700 | 74775 | 139 | 0.000718 | 0.0718 | 7.4 |
| M36 | 4 | 36 | 15.834936 | 1240 | 110289 | 140 | 0.000725 | 0.0725 | 6.5 |
| M42 | 4.5 | 42 | 18.564303 | 2000 | 152383 | 141 | 0.000729 | 0.0729 | 5.8 |
上記の表で何よりも注意すべきは、応力がSUS304の耐力 206（N/mm2 ）よりも 小さいことです。
計算結果は 応力 ＜ SUS304の耐力 を満足しており、標準締付けトルクで 永久変形が発生することはありません。
100mm 当たりの伸びや回転角度 （度）は参考値です。
２章：摩擦力の話に行く。