摩擦力は変動しやすく安定しません。しかし、エネルギーの伝達効率、位置制御性、振動、磨耗劣化等 さまざまな影響をもたらします。
摩擦力をいかにうまく制御するかは、工学関係の雑学として非常に良いテーマです。
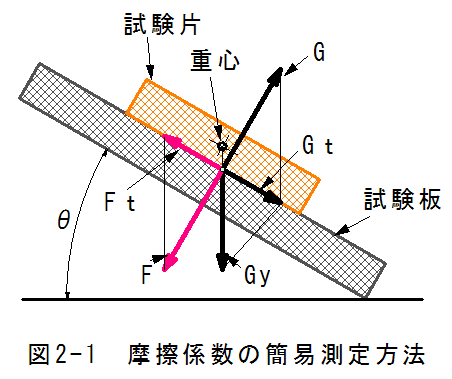
摩擦係数の測定摩擦係数の簡易測定方法を図2-1に示します。
図2-1において、試験片を試験板にのせて、じょじょに傾けていきます。 そして、試験片が動き出す傾斜角度を測定することにより、摩擦係数μを測定できます。
図2-1において、試験片は重心より下方に重力による力Gyを生じます。
試験板からは、下記式の反力を受けます。
G=Gy/COS(θ） ----（2.1）式
試験片は試験板の傾斜方向に
Gt=Gtan（θ） ----（2.2）式
の力が生じます。
試験片と試験板の垂直荷重は
F=G ----（2.3）式
であり、試験板の傾斜方向に生じる摩擦力は
Ft＝μF ----（2.4）式
となります。
θが小さい時は
Ft ＞ Gt ----（2.5）式
となり、静止状態を保ちます。
試験板が動き始める条件は
Ft ＝ Gt ----（2.6）式
（2.6）式、（2.4）式、（2.3）、（2.2）式から
μG＝Gtan（θ） ----（2.7）式
すなわち
μ＝tan（θ） ----（2.8）式
となります。
測定条件としては、基準面が水平である必要があります。
基準面が水平誤差をキャンセルするために左右両方に傾けて 平均値を求めると正確な測定が可能となります。
摩擦係数の変動要因の考察図2-1に示す方法で測定した摩擦係数が一般的な実用条件で安定して再現するのか？
経験的には、安定して再現しないと思っています。
苦い経験としては、焼付きの問題があります。
ステンレスのボルトとナットを強く締めた状態で約300℃程度まで加熱すると 焼付を生じて外れなくなることがあります。
強く締めた状態で約300℃程度まで加熱するとステンレス表面の酸化膜が破壊され ステンレスどうしの結合が生じるためと思います。
同様に同種の金属どうしを潤滑剤無しで荷重をかけて摺動した場合、摩擦熱により 金属どうしの結合が生じる場合があります。
この現象を積極的に利用した技術にアルミ線の超音波ボンディングがあります。 アルミとアルミを加圧しながら、超音波による振動を与えると表面の酸化膜が 破壊して結合します。
ステンレスボルトとナットの表面酸化膜の厚さは必ずしも一定ではありません。 加工直後は薄く、徐々に厚くなると思われます。さらに、大気中で加熱処理を 行うと表面酸化膜が厚くなり、焼付が生じにくくなります。
また、摺動部は全く組成の異なる金属を組み合わせると焼付が生じにくくなります。
摩擦係数は加圧力、表面粗さ、表面形状、汚れ、弾性率等の影響を受け 変動しやすいと考えるべきでしょう。
実用的な摩擦力の測定は、実装状態に近い状態を再現して測定すべきであり、 図2-1に示すような簡易測定のみでは不十分です。
メートルねじの摩擦力測定ねじは、固定用以外に回転運動を直線運動に変換、あるいは直線運動を回転運動に変換 等に用いられます。
運動用ねじは、摩擦係数が大きいと伝達効率が悪化したり、磨耗劣化したりすること が問題となります。
このため、運動用にはボールネジが多く用いられます。実用化された例は聞かないのですが 原理的には静圧ねじも可能です。
１章：メートルネジの規格、締付けトルクと推力で検討した計算式は、ねじの摩擦力測定に 応用することができます。
・締付けトルク＝T
・ねじピッチ＝P
・摩擦係数＝μ
・ねじ有効半径＝R
・ねじ断面傾斜角度＝α
・推力＝Qｙ
Qｙ＝T/（P/（2π) + μR/COS(α）） ---（1.11）式
ねじを緩めるときのトルクTbは
Tb＝Qｙ（P/（2π) - μR/COS(α）） ---（1.12）式
です。ここで、締めるときと緩めるときのトルクの差分ΔTは
ΔT＝T-Tb ---（2.9）式
（2.9）式に（1.12）式と（1.11）式を代入すると
ΔT＝T（1-（P/（2π) - μR/COS(α）/（P/（2π) + μR/COS(α））） ---（2.10）式
（2.10）式を整理すると
ΔT＝T（4πμR/（PCOS(α）+2πμR） ---（2.11）式
（2.11）式を摩擦係数μを求める式に変換すると
μ＝PCOS(α）/（4πR（T/ΔT-0.5）） ---（2.12）式
となります。
（2.12）式において、ΔT＝0のとき計算不能となりますが、 このとき分母が無限大となり、μ＝0となります。
また、T/ΔT＝0.5のとき、分母が無限小となり、μ＝∞となります。
締めるときと緩めるときのトルクを測定すれば、ねじの実装状態での 摩擦係数を測定できることがわかります。
摩擦と推力の関係図一例としてM6のメートルねじの摩擦と推力の関係図を作成します。
M6のメートルねじの標準締付けトルクは5.2N・mですが、この条件で 摩擦係数がゼロの場合、推力が大きくなりすぎて破壊してしまします。
応力がSUS304の耐力206N/mm2となるトルクは0.62N・mです。
従って計算条件は
・締付けトルク：T＝0.62N・m
・ねじピッチ：P＝1mm
・摩擦係数：μ＝0〜1.0
・ねじ有効半径：R＝2.675mm
・ねじ断面傾斜角度：α＝30°
とします。
摩擦と推力の関係図を図2-2に示します。
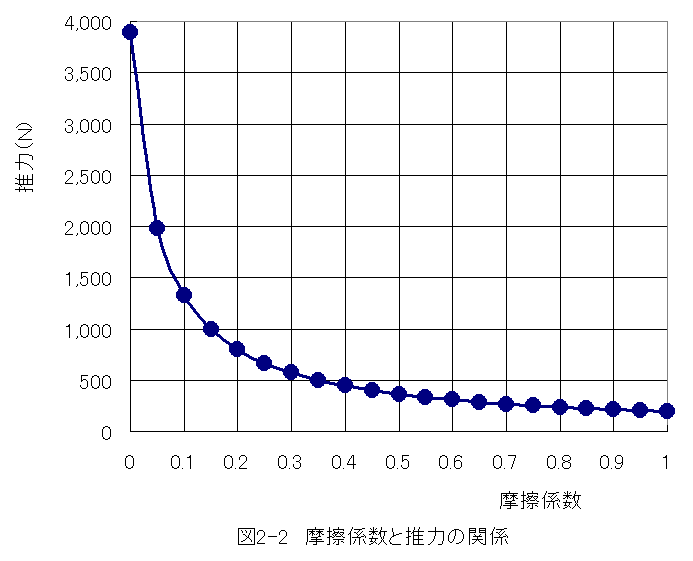
図2-2から、摩擦係数が0〜0.05の間で、推力が大幅に減少することが わかります。
推力の減少はエネルギーの伝達効率と等しく、失われたエネルギーは 摩擦熱となります。
エネルギーの伝達を考慮した場合、摩擦係数は0.05以下が必要なことが わかります。
差分トルクと摩擦係数の関係図一例としてM6のメートルねじの摩擦と推力の関係図を作成します。
M6のメートルねじの標準締付けトルクは5.2N・mですが、この条件で 摩擦係数がゼロの場合、推力が大きくなりすぎて破壊してしまします。
応力がSUS304の耐力206N/mm2となるトルクは0.62N・mです。
従って計算条件は
・締付けトルク：T＝0.62N・m
・差分トルク：ΔT＝0〜1.2N・m
・ねじピッチ：P＝1mm
・ねじ有効半径：R＝2.675mm
・ねじ断面傾斜角度：α＝30°
とします。
差分トルクと摩擦係数の関係図を図2-3に示します。
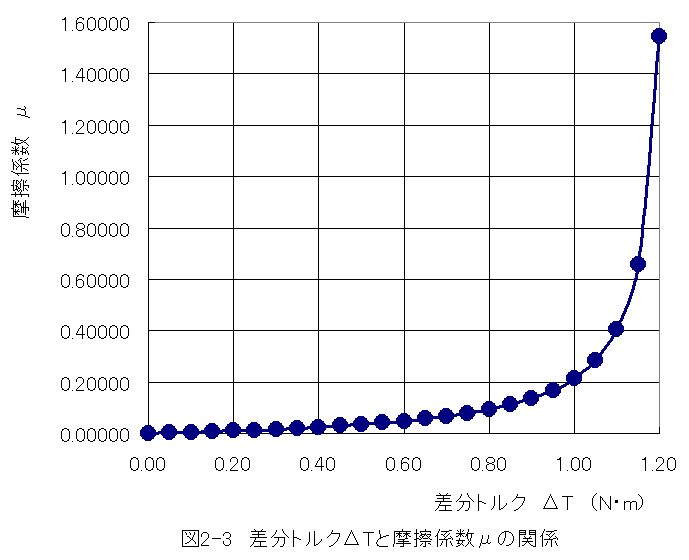
図2-3から、差分トルクがΔT＝1.00〜1.2N・mの範囲で摩擦係数が急激に変化することが わかります。
逆に差分トルクがΔTが小さい時は摩擦係数の変化が少なく、より正確に摩擦係数の測定が可能である ことがわかります。
３章：摩擦力の制御に行く。