１１章：台形近似積分による梁の撓み解

    作成2011.11.24
  1. 　梁の基礎方程式は
    　梁の撓みの基礎方程式は

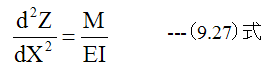
    　梁の応力の基礎方程式は

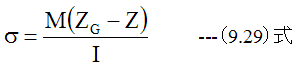
    　として与えられます。（9.27）式を代数的に解くのはさほど難しいことではありませんが、集中荷重点や断面形状が変化する点で式が不連続となります。
    　不連続点では境界条件を一致させる必要があり、多点集中荷重や断面形状が変化する梁のモデルの代数解を求める作業が煩雑となります。

    　台形近似積分を使用すると、多点集中荷重や断面形状が変化する梁のモデルの計算を容易に行うことができます。


  2. 　台形近似積分による梁の撓み解法
    　予め
    ・縦弾性係数　E
    ・断面2次モーメント　I
    ・重心距離　Zu＝Zg-Z
    ・モーメント　M
    　は求めておきます。
    　　X=0　における初期値

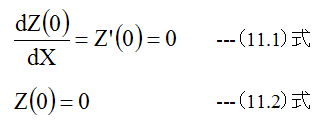
    　として、計算を開始します。2番目以降は整数iに対して以下の計算を実施します。

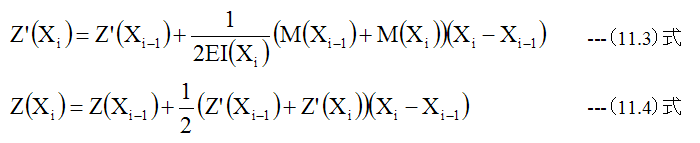
    　（11.3）式、 （11.4）式において、縦弾性係数（E）は定数、断面2次モーメント（I）はXの関数、モーメント（M）はXの関数としています。
    　Xの変化する間隔は必ずしも等間隔である必要はありません。Xiの値が最終端まで達したら、計算が終了します。

    　最後に初期条件の最適化を行う必要があります。X=0における傾斜角度Z'＝0、高さZ=0としたためであり、各梁のモデルの境界条件 に合わせて、初期条件を最適化する必要があります。

    　初期条件の最適化処理はEXCELの「ツール」＿「ゴールシーク」の機能を使用します。
    　 「ツール」＿「ゴールシーク」を選択し、「数式入力セル」にモデルの境界条件セルを設定、「目標値」に境界条件値、 「変化させるセル」に初期条件セルを設定し最適化を実施します。


  3. ワークブック「2台形近似梁計算.xls」のダウンロード
    　下記のワークブック「台形近似梁計算.xls」をダウンロードしてください。

    　ダウンロード後はダブルクリックで解凍してから使用してください。
    　     ワークブック「台形近似梁計算.xls」をダウンロードする。


  4. 台形近似積分による片持梁の撓み解
    　計算条件として、
    ・縦弾性率　E=193000（N/mm2）
    ・梁の幅　B=10mm
    ・梁の厚さ　H=2mm
    ・梁の長さ　L=100mm
    ・荷重　　　　W=10N
    　とします。断面2次モーメントは

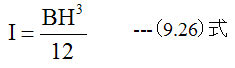
    　重心距離（Zg)は

    　モーメントは

    　を設定します。
    　X=0の初期条件（ピンクセル）にｄZ/dX=0、Z=0を設定した場合、X=100mmにおいて、ｄZ/ｄX=0.0389、Z=1.2970mmとなります。
    　片持梁の境界条件として、 X=100mmにおいて、ｄZ/ｄX=0、Z=0mmでなければなりません。
    　以下の手順で初期条件を最適化します。
    1. EXCELの「ツール」＿「ゴールシーク」を選択します。
    2. 「数式入力セル」にモデルのX=100mmのｄZ/ｄXセルを設定、「目標値」に0、「変化させるセル」にX=0のｄZ/ｄXセルを設定し最適化を実行します。
    3. EXCELの「ツール」＿「ゴールシーク」を選択します。
    4. 「数式入力セル」にモデルのX=100mmのZセルを設定、「目標値」に0、「変化させるセル」にX=0のZセルを設定し最適化を実行します。
      　以上で初期条件の最適化処理は完了です。

    　最適化処理実行結果を以下に示します。



  5. 代数解と台形近似計算の比較
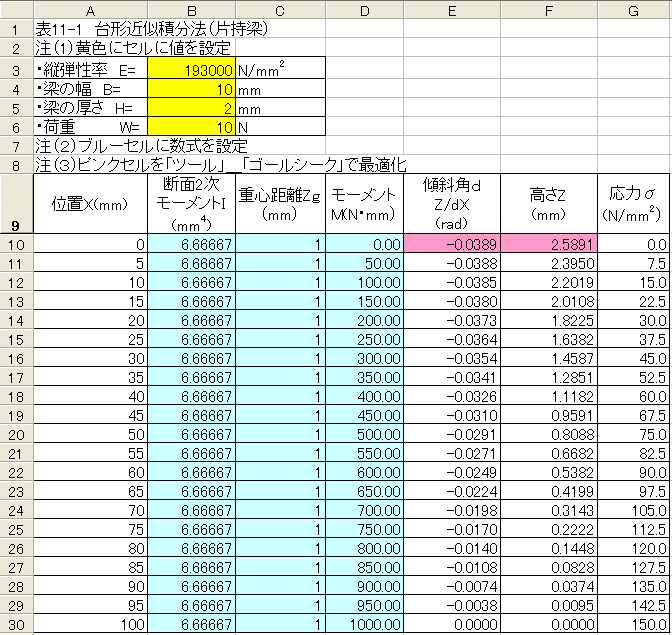
    　代数解と台形近似計算の比較を以下に示します。


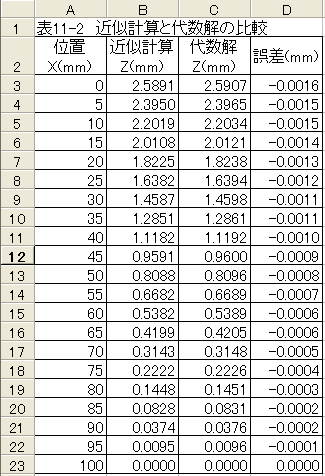
    　上記の表からわかるように、代数解と台形近似計算の値は良く一致していることがわかります。


  6. 断面が変化する多点集中荷重梁


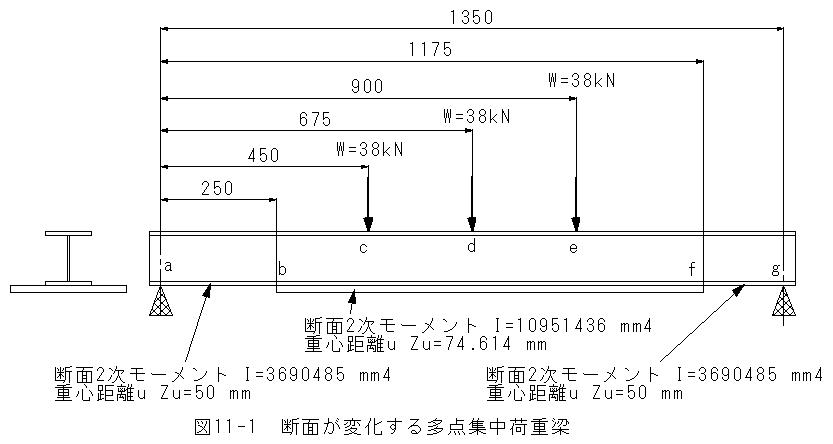
    　図11-1に示すような断面が変化する多点集中荷重梁のモデルにおいて、台形近似積分による梁の撓み解法は威力を発揮します。
    　梁の撓みの基礎方程式は断面が変化する点や荷重点で式が不連続となるため、代数解を求める手順が複雑化します。しかし、 台形近似積分による梁の撓み解法は不連続点の処理が容易になります。

    　梁の材料はSS400とします。
    ・縦弾性率　E=210000（N/mm2）
    ・耐力　205 （N/mm2）以上
    　です。
    ・荷重Wは3箇所とも38000Nで合計114000N（約11.4ｔ）とします。
    1. aｃ間のモーメントMは

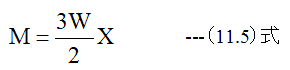
    2. ｃｄ間のモーメントMは

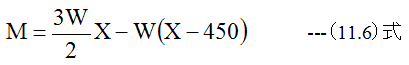
    3. de間のモーメントMは

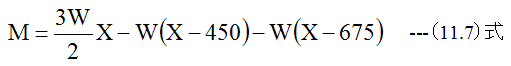
    4. eg間のモーメントMは

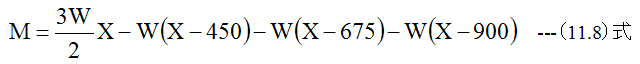
      　となります。

    1. 断面2次モーメントの変化も考慮して、計算表を作成します。
    2. 不連続点では、不連続点から僅かにずらして、はさむようにXの値を設定します。
    3. X=0の初期条件（ピンクセル）にｄZ/dX=0、Z=0を設定した場合、X=1350mmにおいて、ｄZ/ｄX=0.0135、Z=9.104mmとなります。
    4. 単純支持梁の境界条件として、 X=1350mmにおいて、Z=0mmでなければなりません。
      　以下の手順で初期条件を最適化します。
    5. EXCELの「ツール」＿「ゴールシーク」を選択します。
    6. 「数式入力セル」にモデルのX=1350mmのZセルを設定、「目標値」に0、「変化させるセル」にｄZ/ｄX=0のZセルを設定し最適化を実行します。
      　以上で初期条件の最適化処理は完了です。

    　最適化処理実行結果を以下に示します。


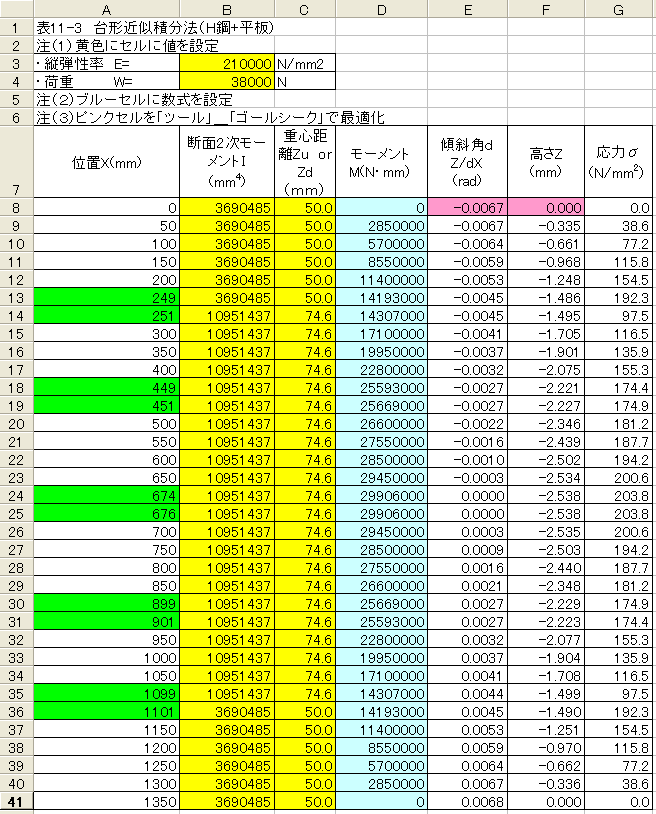
    　上記の表において、最大撓みは-2.54mm（下方向撓み）、最大応力は203.8N/mm2でS400の耐力205N/mm2 以内となっています。
    　したがって、図11-1に示す梁の最大許容荷重は合計114000N（約11.4ｔ）ということになります。


  7. 台形近似積分による梁の撓み解のまとめ
    　実用的な梁の構造において、必ずしも断面形状は均一ではありません。また、荷重点は1点とは限りません。
    　このような梁の場合、公式を見つけるのは容易ではありません。従って、基礎方程式から代数解を求める 必要が生じます。しかし、この手順は複雑で厄介です。
    　台形近似積分による梁の撓み解法は公式が見つからない場合の、解決策として極めて有効です。







12章：せん断応力と組合せ応力に行く。

トップページに戻る。