梁の基礎方程式
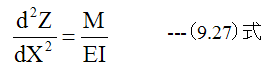
の誘導の過程において、せん断応力の影響を無視していることを忘れてはいけません。通常の梁の 撓みにおいては、曲げモーメント（M)が支配的であり、せん断応力の影響は小さくなります。
しかし、特殊条件においては、せん断応力の影響が無視できなくなります。
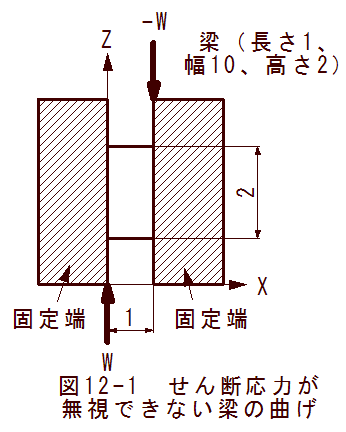
せん断応力が無視できない梁の曲げ図11-1にせん断応力が無視できない梁の曲げの例を示します。
計算条件として
・縦弾性率 E=193000 N/mm2
・梁の幅 B=10 mm
・梁の厚さ H=2mm
・荷重 W=2000 N
として、図11-1示す曲げの解を求めます。
- 曲げモーメント線図
曲げモーメントは以下のグラフのようになります。
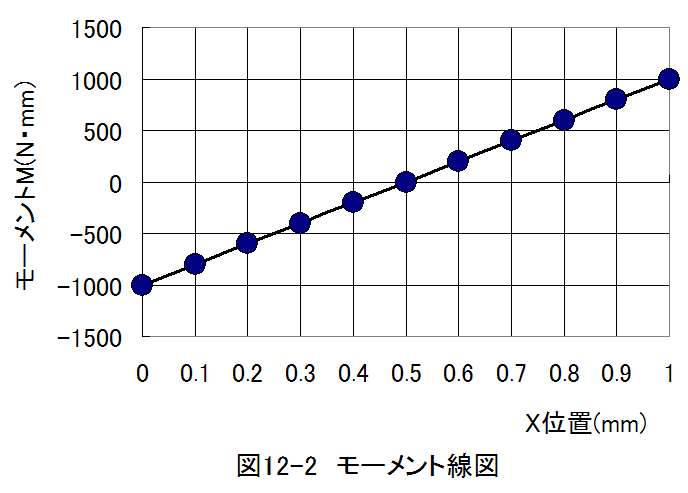
- 撓み量線図
撓み量線図は以下のグラフのようになります。
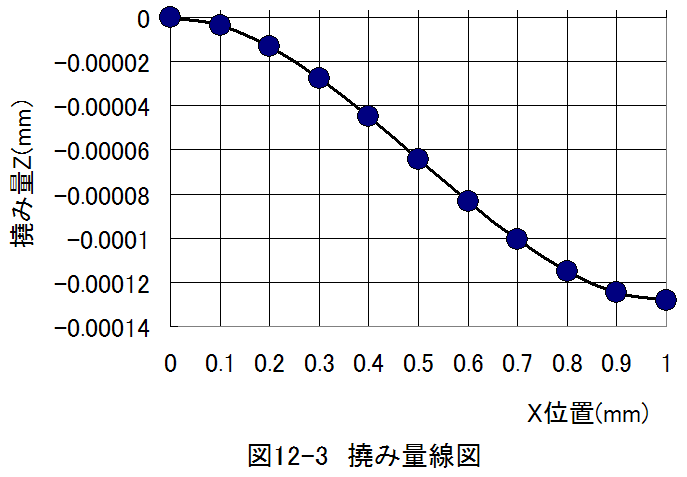
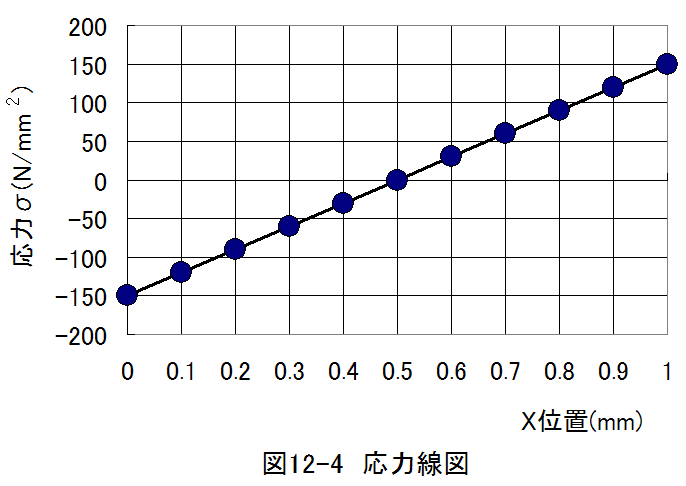
- 応力線図
応力線図は以下のグラフのようになります。
- せん断応力τ
せん断応力τの値は
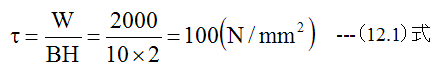
- せん断応力による歪γ
せん断弾性係数G=78500(N/mm2)
歪γの値は
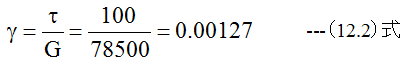
- せん断応力による変形量Z
梁の長さL=1mmとして
変形量Zの値は
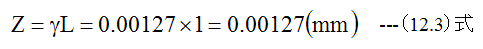
- 曲げ応力による変形量とせん断応力による変形量の比較
曲げ応力による変形量Z=0.000128mm
せん断応力による変形量＝0.00127mm
となり、せん断応力による変形量が曲げ応力による変形量の約10倍となりことがわかります。
図11-1に示す条件においては、せん断応力が支配的になることがわかります。
- せん断応力の応用
せん断応力は主にせん断加工に利用されます。身近な応用はハサミです。この例からわかるように、 梁の長さが小さくなるほどせん断応力が支配的になり、せん断加工がしやすくなります。
2枚のはさみの刃の隙間が大きくなると薄い紙が切れにくくなるのはこのためです。
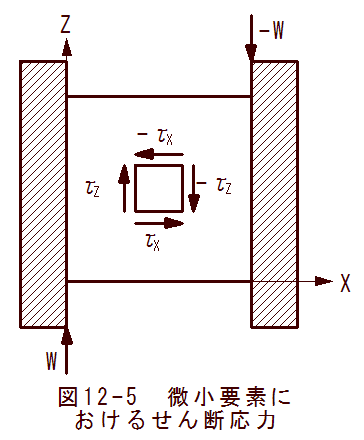
微小要素におけるせん断応力図11-5に微小要素におけるせん断応力の状態図を示します。
図11-5において、梁の中心位置でモーメントがゼロとなり曲げ応力がゼロとなります。
このような位置では純粋のせん断応力のみが作用します。
矩形の微小要素を考えた場合、Z方向のせん断応力のみですとモーメントが発生し、 力のバランスがとれなくなります。
Z方向のせん断応力で発生するモーメントを打ち消すためにX方向にもせん断応力が発生します。
これを共役せん断応力といいます。
XZ平面での共役せん断応力をτxzとした場合
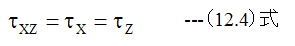
が成立します。
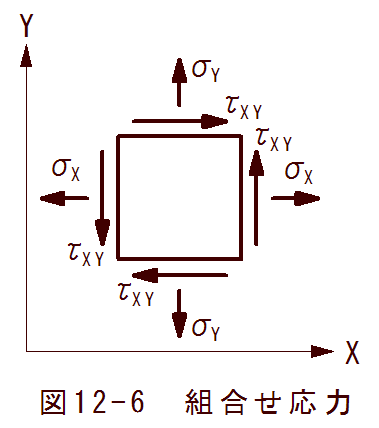
組合せ応力XYZ座標系において、図11-6に示すようなXY平面上の要素に加わる組合せ応力について考えます。
前提条件として、Z方向応力、XZ平面せん断応力、YZ平面せん断応力はゼロとします。すなわち
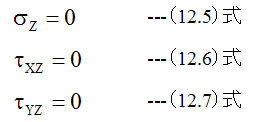
垂直応力による歪は、ポアソン比＝νとして
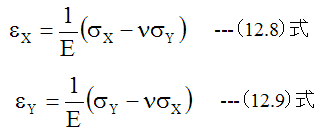
せん断応力による歪は
となります。 （12.8）式、 （12.9）式、（12.10）式を変形して
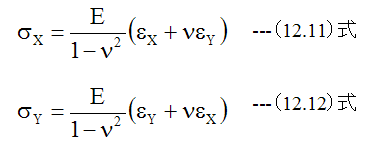
が得られます。
（12.11）式、 （12.12）式、 （12.13）式は２次元的な組合せ応力と歪の関係式です。式からわかるように、 X方向とY方向の垂直応力はポアソン比（ν）をパラメータとして相互に関係しあっています。
３次元の組合せ応力も、同様な方法で関係式を導くことができます。しかし、円筒や円板の変形を 検討する場合は、 ２次元的な組合せ応力として扱うことが可能です。
１３章：円筒の応力と変形に行く。