圧力容器は、製作のしやすさから円筒形にすることが多い。設計した圧力容器の耐圧や変形を大まか
に予測する必要が生じます。
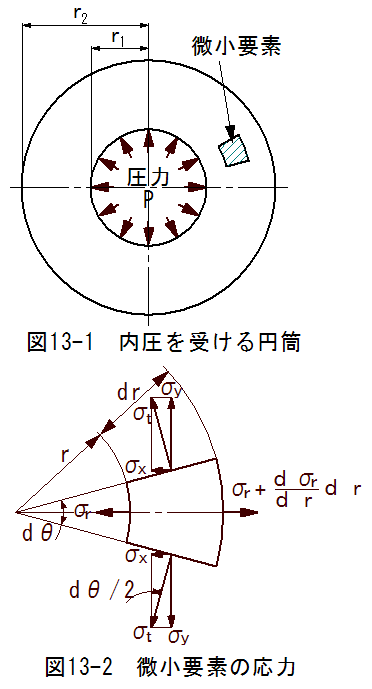
内圧を受ける円筒の応力と変形図13-1に内圧を受ける円筒の断面図を示します。円筒の微小要素を切り出し、応力の状態を示したの が図13-2です。
図13-2に示した、応力のバランス図は円筒の長さ方向に生じる応力が省略してあります。
厳密ではありませんが、ここでは円筒の長さ方向の応力はゼロと仮定して検討します。
図13-2に示す半径方向の力のバランスは
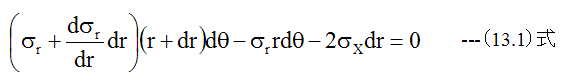
となります。また
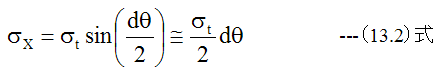
の関係式が成立します。 （13.1）式に（13.2）式を代入して、整理すると
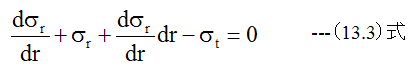
微小項を無視すると
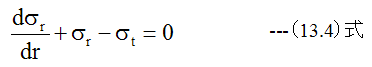
が得られます。 （13.4）式は半径方向の応力のバランス条件式です。応力が半径ｒの関数として与えら れれば方程式を解くことが可能ですが、このままでは解けません。
そこで変形の条件を考えます。変形も中心軸に対して対称ですから、半径ｒの円周は一様に伸縮 します。半径ｒにおける半径方向に変位をuとするならばr+drにおける変位は
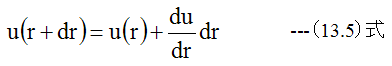
従って半径方向の歪は
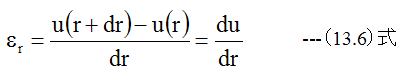
また、円周方向の歪は
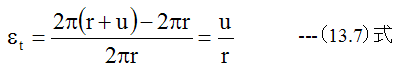
となります。
ここで２次元応力の関係式
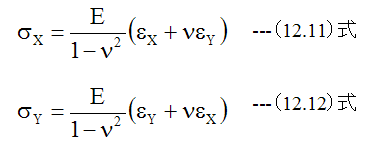
を使用します。X=ｒ、Y=ｔとして、 （12.11）式、 （12.12）式に（13.6）式、 （13.7）式を代入すると
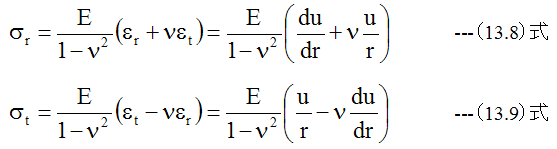
（13.4）式に（13.8）式、 （13.9）式を代入して整理すると下記のｕとｒに関する微分方程式が得られます。
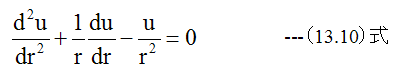
（13.10）式を代数的に解くため下記のように変形します。
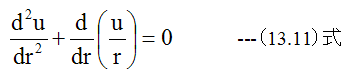
積分して
（13.12）式を変形して
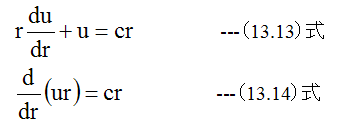
積分して
c1＝c/2として変形すると
微分すると
（13.8）式、 （13.9）式に（13.16）式、 （13.17）式を代入して、下記に示す一般解が得られます。
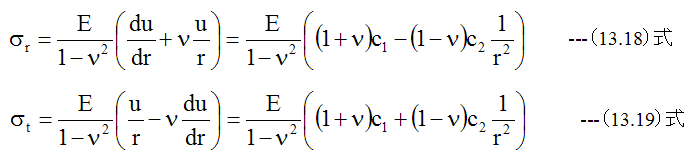
次に境界条件をいれて積分定数ｃ1とｃ2を求めます。
r=r1において
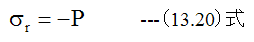
r=r2において
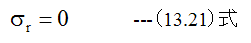
（13.18）式に（13.20）式と（13.21）式を代入して
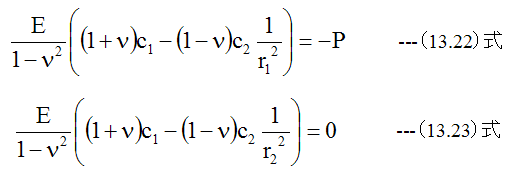
（13.22）式、 （13.23）式から
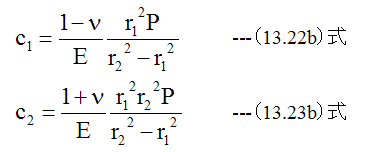
ここで
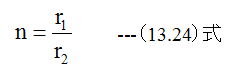
とすると
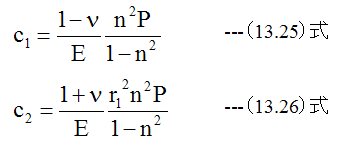
（13.18）式、 （13.19）式に（13.25）式、 （13.26）式を代入すると
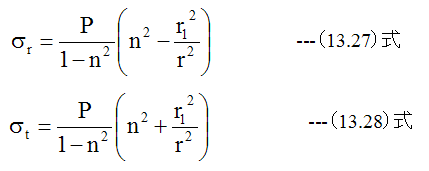
となります。半径ｒの点の半径方向変位Uは、（13.16）式に（13.25）式、 （13.26）式を代入して得られます。
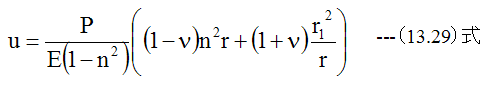
外圧を受ける円筒の応力と変形以下の境界条件をいれて積分定数ｃ1とｃ2を求めます。
r=r1において
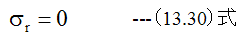
r=r2において
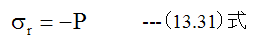
（13.18）式に（13.30）式と（13.31）式を代入して
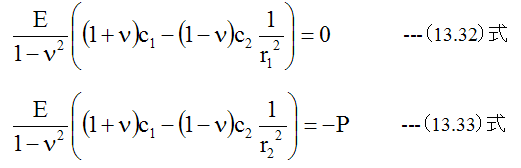
（13.32）式、 （13.33）式から
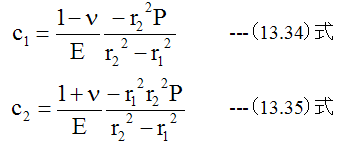
ここで
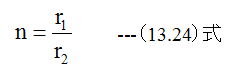
とすると
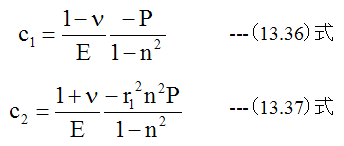
（13.18）式、 （13.19）式に（13.36）式、 （13.37）式を代入すると
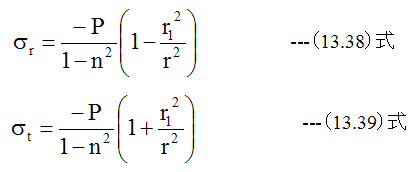
となります。半径ｒの点の半径方向変位Uは、（13.16）式に（13.38）式、 （13.39）式を代入して得られます。
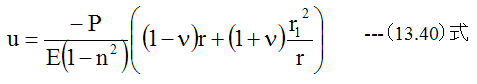
内圧を受ける円筒の応力と変形の計算例配管用ステンレスパイプ 32A(1-1/4B)TPSスケジュール40（外形Φ42.7 厚さ3.6）SUS304を使用するとします。
・縦弾性係数 193000 N/mm2
・ポアソン比 0.3
・耐力 206 N/mm2以上
・加圧圧力は、最大応力が耐力 206 N/mm2に達する圧力とします。
内圧が加わった場合の計算結果を下記表に示します。
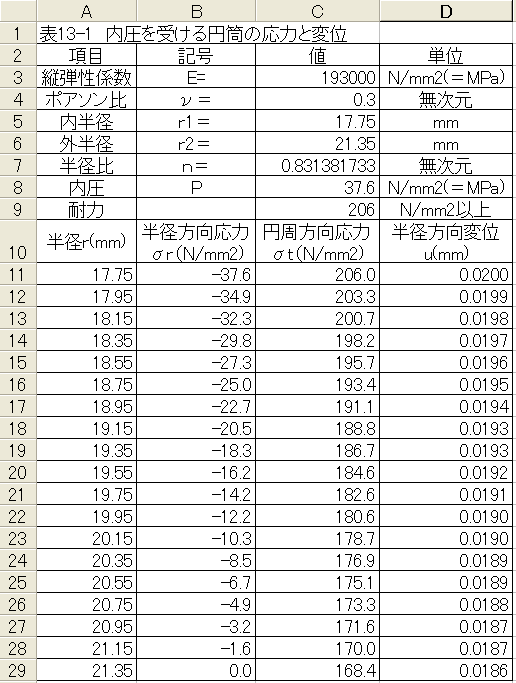
・内圧が加わった場合、圧力が37.6MPaでSUS304の耐力に達します。
・半径方向応力はマイナスとなり圧縮応力となります。圧縮応力は内壁で最大で外壁でゼロとなります。
・円周方向応力はプラスで引張応力となります。引張応力は内壁で最大となります。
・半径方向変位はプラスで半径が増大する方向に変形します。
外圧を受ける円筒の応力と変形の計算例配管用ステンレスパイプ 32A(1-1/4B)TPSスケジュール40（外形Φ42.7 厚さ3.6）SUS304を使用するとします。
・縦弾性係数 193000 N/mm2
・ポアソン比 0.3
・耐力 206 N/mm2以上
・加圧圧力は、最大応力が耐力 206 N/mm2に達する圧力とします。
外圧が加わった場合の計算結果を下記表に示します。
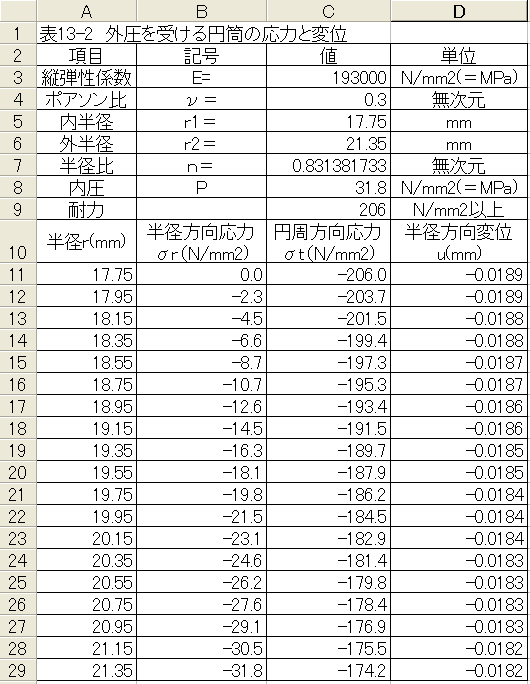
・外圧が加わった場合、圧力が31.8MPaでSUS304の耐力に達します。 ・半径方向応力はマイナスとなり圧縮応力となります。圧縮応力は内壁がゼロで外壁で最大となります。 ・円周方向応力はマイナスで圧縮応力となります。圧縮応力は内壁で最大となります。 ・半径方向変位はマイナスで半径が縮小する方向に変形します。
ワークブック「円筒応力.xls」のダウンロード下記のワークブック「円筒応力.xls」をダウンロードできます。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「円筒応力.xls」をダウンロードする。円筒の応力と変形まとめ円筒の応力と変形においては2次元方向からの応力がかかるため、計算式の誘導がかなり複雑です。
配管用ステンレスパイプ 32A(1-1/4B)TPSスケジュール40（外形Φ42.7 厚さ3.6）SUS304の耐圧 は31.8MPaとなります。これは、水深に換算すると水深3000mでの水圧に相当します。水深3000m以上 の深海においては水圧でステンレスパイプがつぶれてしまうことになります。
水深3000m以上の深海を探索する潜水艦は、かなり強固な構造にしないと強度が持たないことになります。
14章：2次元応力を考慮した平板の曲げに行く。