1次元曲げモーメントの場合の平板の曲げ1次元曲げモーメントの梁の曲げにおいては、通常応力も1次元で扱うことが一般的で多くの場合、 下記の基礎方程式が用いられます。
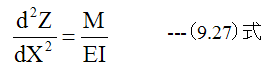
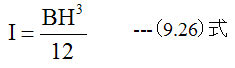
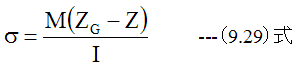
上記の式は、応力が1次元方向のみに作用することを前提としており、扱いやすいため多く場合で使用されます。しかし 、厳密に考えると応力は2次元方向に発生します。 2次元応力を考慮した平板の曲げについて検討して みたいと思います。
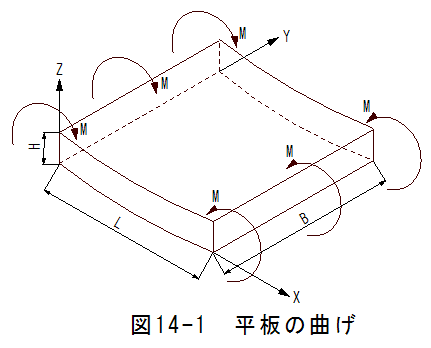
図14-1は1次元曲げモーメントのみが作用する平板の状態を示しています。ここでY軸のまわ りの単位長さ当たりのモーメントMyは
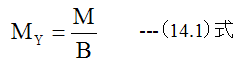
中立軸の曲率半径をRとした場合、X軸方向の歪εxは
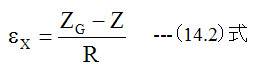
次にY方向の歪εｙとZ方向の応力σｚは、下記の条件式が成立するとします。
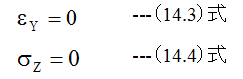
ここで下記の関係式を使用します。
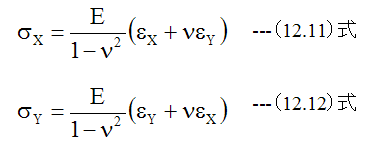
（12.11）式、 （12.12）式に（14.2）式、（14.3）式を代入します。
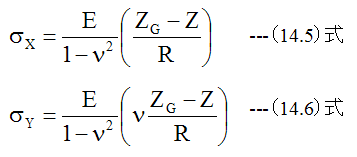
（14.6）式は上記の条件において、Y方向の応力が発生することを示しています。
応力によるモーメントの総和（M）は
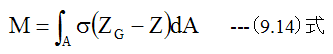
σ＝σxとして、 （9.14）式に（14.5）式を代入すると
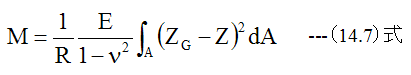
ここで
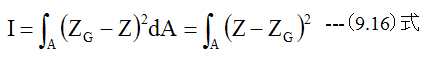
の定義式（9.16）式を（14.7）式に代入して整理すると
となります。また
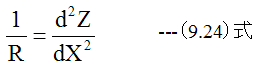
（9.24）式を（14.7）式を代入すると
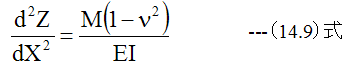
2次元応力を考慮した平板の曲げの基礎方程式を得ることがで きます。また単位長さあたりの曲げモーメントの式（14.1）式を代入すると
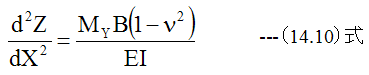
となります。また下記の定義式
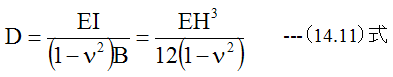
を使用すると（14.10）式は
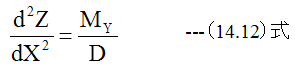
となります。Dを板の曲げ剛性といいます。 （9.27）式と（14.9）式を比較すれば明らかなように、 2次元応力を考慮した場合の撓み量は（1-ν2）倍と小さくなります。
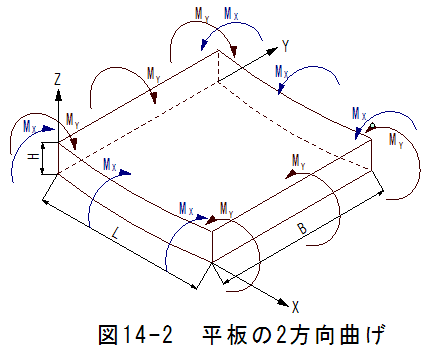
互いに直交する2方向への曲げ図14-2に互いに直交する2方向への曲げの状態を示します。
図14-2において、MxはX軸のまわりの単位長さあたりのモーメ ントであり、MｙはY軸のまわりの単位長さあたりのモーメントです。
中立軸のX方向曲率半径をRｘとした場合、X軸方向の歪εxは
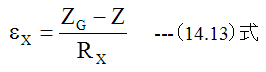
中立軸のY方向曲率半径をRｙとした場合、Y軸方向の歪εｙは
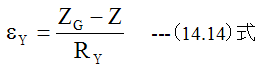
ここで下記の関係式を使用します。
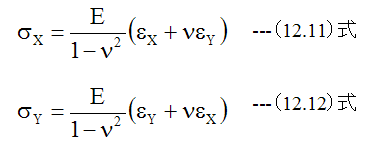
（12.11）式、 （12.12）式に（14.13）式、（14.14）式を代入します。
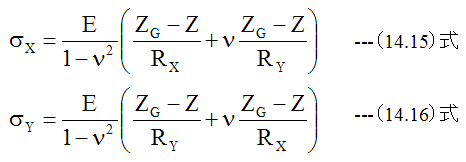
応力によるモーメントの総和（M）は
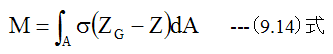
ですので、X方向モーメントMxとY方向モーメントMyは
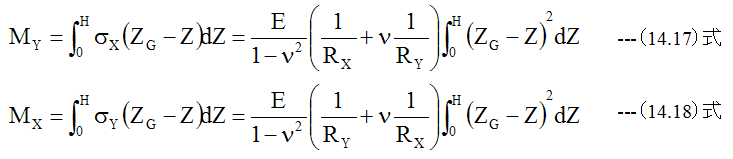
ここで
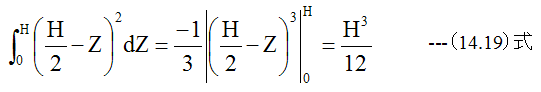
（14.17）式、 （14.18）式に（14.19）式を代入すると
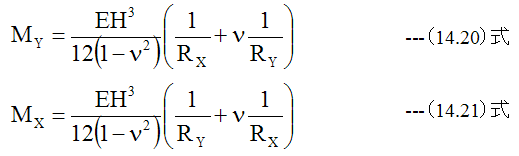
ここで
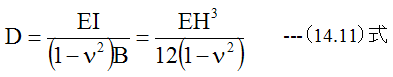
（14.20）式、 （14.21）式に（14.11）式を代入すると
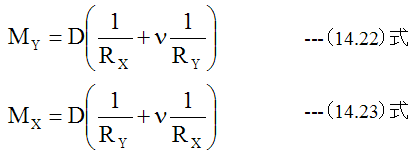
次に下記の曲率半径関係式を使用します。
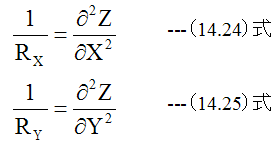
（14.22）式、 （14.23）式に（14.24）式と（14.25）式を代入すると
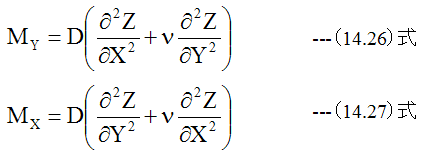
（14.26）式と（14.27）式が互いに直交する2方向への曲げの基礎方程式です。
（14.22）式と（14.23）式を（14.15）式、 （14.16）式に代入すると
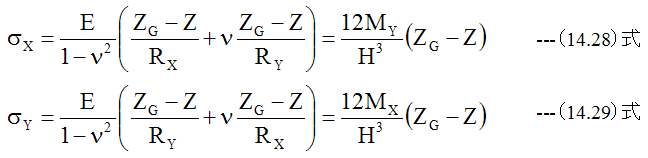
となります。 （14.28）式、 （14.29）式は応力を与える式であり、Zgは重心位置です。
2次元応力を考慮した平板の曲げのまとめ互いに直交する2方向への曲げにおいて、基礎方程式は一対の偏微 分方程式となることがわかりました。具体的なモデルの解を求めるには、 一対の偏微分方程式を解く必要があり容易ではなさそうです。
１５章：円板の軸対称曲げに行く。