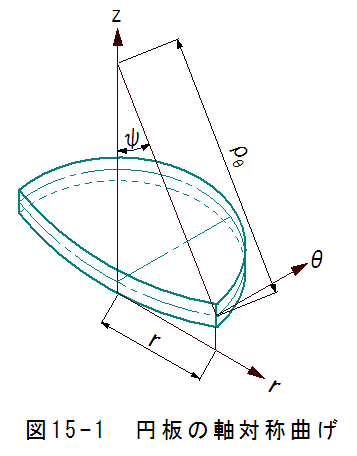
円板の軸対称曲げの基礎方程式図15-1に円板の軸対称曲げの説明図を示します。
ここでは、座標軸を上方にｚ、半径方向をｒ、円周方向をθとします。
軸対称曲げにおいては、z軸を中心に円周方向は均一に変形するものとしています。
曲げの曲率半径の記号は、半径方向ｒと区別するために、円周方向の曲率半径をρθ 、半径方向の曲率半径をρrとします。
図15-1において。位置ｒにおける面の法線とｚ軸とのなす角をψとします。ここで
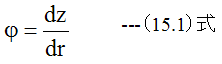
の関係が成立します。また
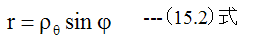
であり、sinψ≒ψとするならば
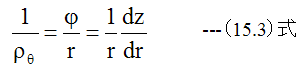
次に半径方向の曲率半径ρrは
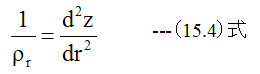
が成立します。ここで互いに直交する2方向への曲げにおける曲げモーメントの式を利用します。
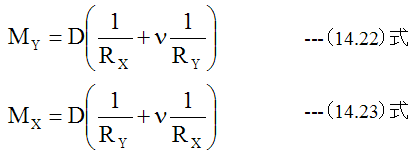
（14.22）式、 （14.23）式をMy＝Mθ、Mx＝Mr、Rx＝ρｒ、Ry＝ρθと変数変換をします。次に（15.3）式 と（15.4）式を代入するならば
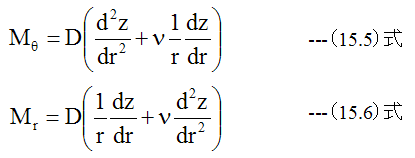
となります。
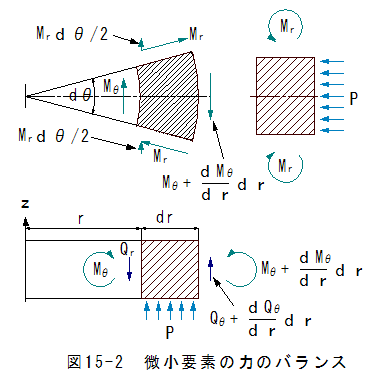
微小要素の力のバランスここで、微小要素の力のバランスを考えます。
図15-2において、圧力Pはz軸の正方向に等分布荷重を与えます。
圧力Pはせん断力Qｒの変化を与え、せん断力QｒはモーメントＭθの変化を生じます。
ここで、垂直方向の力のバランスから
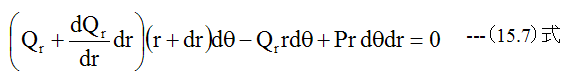
高次の微小項を無視して整理すれば
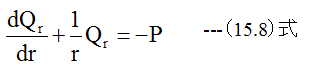
次にモーメントの釣合いを考えますが、モーメントには方向性がありベクトル表 示して、位置r+drでのθ方向成分のバランスを考えます。
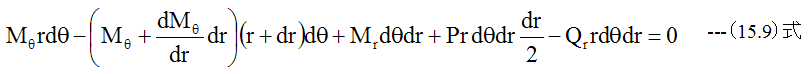
高次の微小項を無視して整理すれば
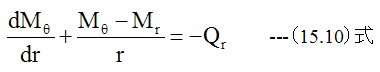
（15.10）式に（15.5）式と（15.6）式を代入すると
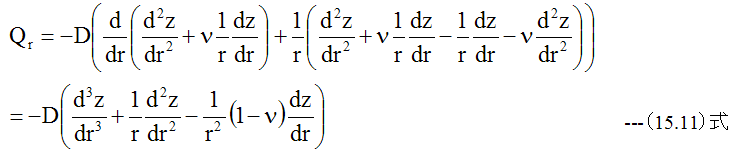
ここで、下記の微分公式を適用するため、（1-ν）≒1の近似を行います。
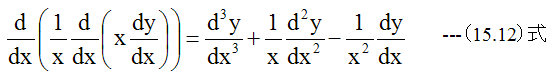
代数解が得られる微分方程式は限られているのですが、 （15.12）式の形の 微分方程式は代数解を得ることができます。
したがって、 （15.11）式は
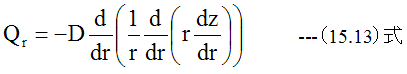
ここで（15.8）式を下記のように変形します。
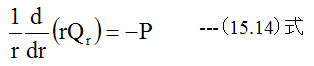
（15.14）式に（15.13）式を代入すると
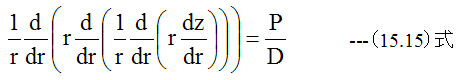
が得られます。（15.15）式が円板の軸対称曲げの基礎方程式です。 （15.15）式は順次 積分が可能な形をしており代数解を得ることができます。
代数解はｃ1、ｃ2、ｃ3、ｃ4を定数として
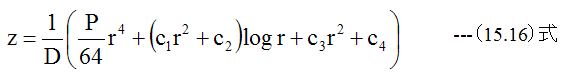
（15.16）式において
ｃ1＝せん断力の初期値（集中荷重があるとき有限の値、集中荷重が無いときゼロ）
ｃ2＝曲率半径の初期値（リング内径がｒ＝0の場合は特異点のためｃ2＝0）
ｃ3＝傾き角度の初期値
ｃ4＝変位ｚの初期値
の定数を決定する必要があります。
周辺を固定され等分布荷重を受ける円板（15.13）式に（15.16）式を代入して整理します。
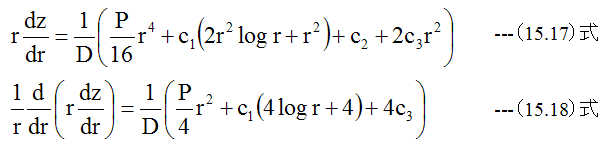
ゆえに
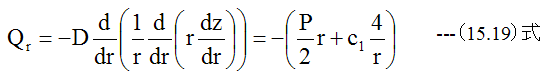
半径ｒの全円周のせん断力Qsは
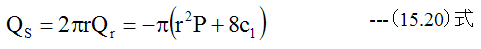
半径ｒの範囲内の全荷重Wpは
全荷重Wpと全円周のせん断力QsはWp＝- Qsが成立する必要があります。従って
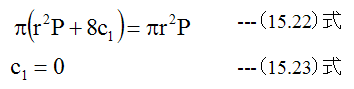
次に定数ｃ2ですが、 （15.16）式はｃ2がゼロ以外の場合、ｒ＝0でlogRの値がマイナス 無限大となり計算不能となります。円板の場合はｒ＝0が存在するためｃ2はゼロ以外の値を取れなくなります。
もし、円板でなくリング板の場合は、ｃ2が有限の値をとることができます。今回は円板を想定しているため
となります。
次に円板の半径がr=aで周辺固定の場合、 r=aで傾きがゼロである必要があります。すなわち
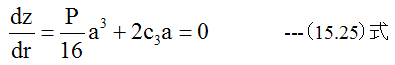
ゆえに
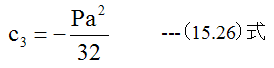
また、 r=aで変位ｚがゼロである必要があります。すなわち
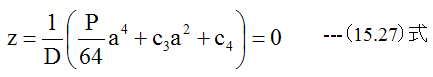
（15.27）式と（15.26）式から
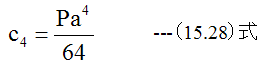
（15.16）式に定数を代入すると
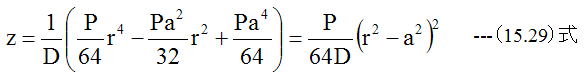
となります。ここで下記式を代入すると
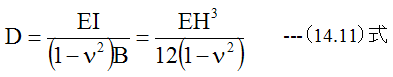
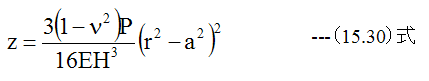
となります。曲げモーメントは（15.5）式、 （15.6）式に（15.30）式を代入して
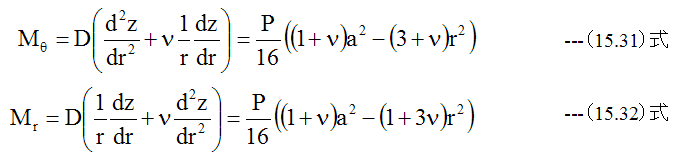
曲げ応力はσｒ＝σｘ、σθ＝σｙMθ＝Mｙ、Mr＝Mxとして下記式に（15.31）式、 （15.32）式を代入して求めることができます。
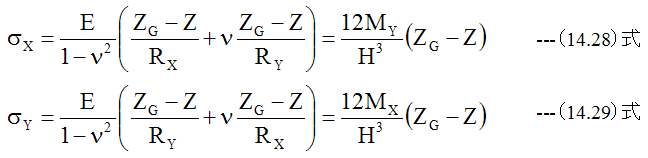
すなわち
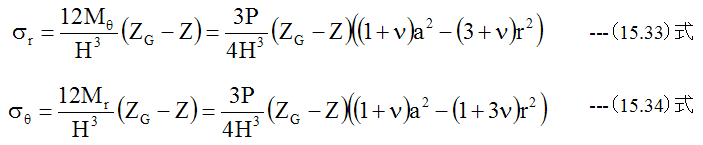
となります。
周辺を固定され中心に集中荷重Wを受ける円板分布荷重P=0を（15.16）式に代入する
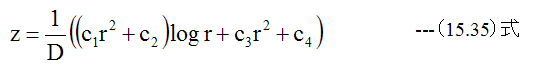
半径ｒの全円周のせん断力Qsは
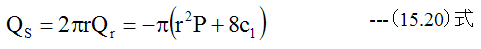
集中荷重Wと全円周のせん断力QsはW＝- Qsが成立する必要があります。従って
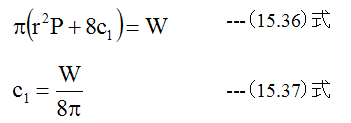
となります。c2は周辺を固定され等分布荷重を受ける円板と同様に
となります。従って（15.35）式は
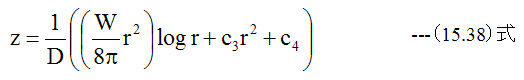
次に円板の半径がr=aで周辺固定の場合、 r=aで傾きがゼロである必要があります。すなわち
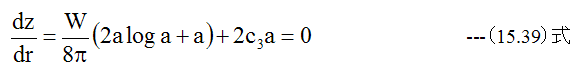
ゆえに
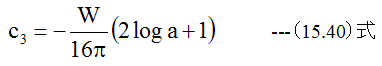
また、 r=aで変位ｚがゼロである必要があります。すなわち
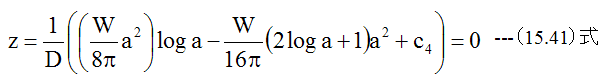
ゆえに
（15.38）式に定数を代入すると
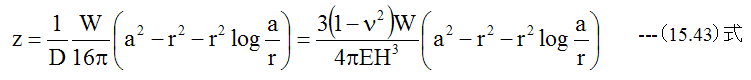
となります。曲げモーメントは（15.5）式、 （15.6）式に（15.43）式を代入して
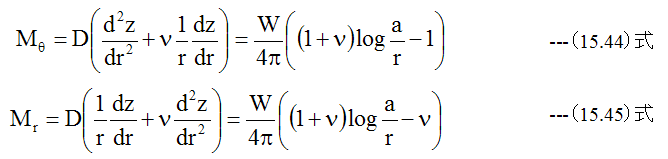
曲げ応力はσｒ＝σｘ、σθ＝σｙMθ＝Mｙ、Mr＝Mxとして（14.27）式、 （14.28）式に （15.44）式、 （15.45）式を代入して求めることができます。
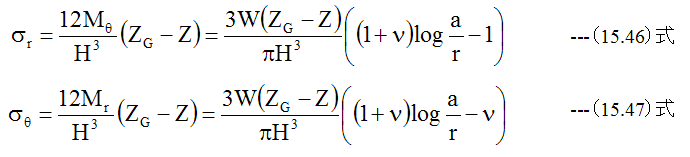
円板の軸対称曲げの一般解円板の軸対称曲げの一般解は
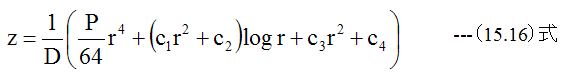
として与えられますが、4個の定数を境界条件から決定する必要があります。 4個の定数 はモデルの境界条件にり変わるため、境界条件に応じて決定する必要があります。
4個の定数の決定のための式の変形はけっこう大変ですね！！
円板の板厚計算事例配管用ステンレスパイプ 32A(1-1/4B)TPSスケジュール40（外形Φ42.7 厚さ3.6）SUS304を使用するとします。
・内径 35.5mm
・縦弾性係数 193000 N/mm2
・ポアソン比 0.3
・耐力 206 N/mm2以上
・圧力 31.8 N/mm2
・周辺支持条件 厳密ではありませんが周辺固定支持と仮定します。
・最大応力が耐力 206 N/mm2に達する円板の板厚を求めます。
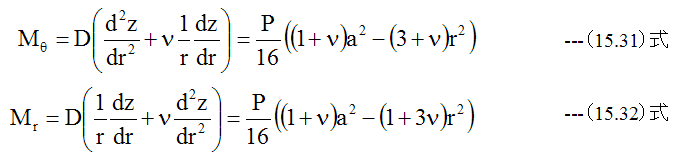
上記の式においてモーメントはｒ＝aにおいて最大となります。最大モーメントMmaxは
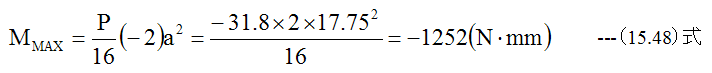
最大応力は下記式より求めることができます。
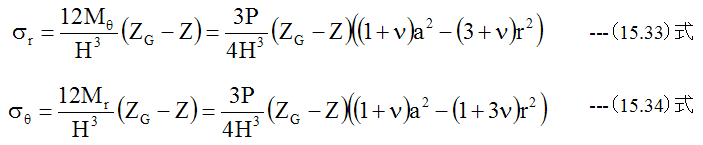
Zg-Z＝H/2とするならば
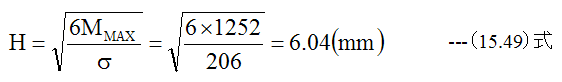
となり、以外に簡単に求まります。パイプの厚さ3.6ｍｍに対して底板の円板厚さは6.04ｍｍと 約2.4ｍｍ厚くする必要があることがわかります。
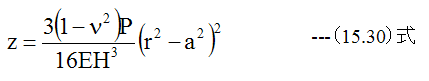
円板の撓み量は上記の式で与えられ、ｒ＝0で最大撓みとなります。
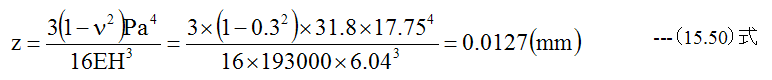
撓み量は圧力の方向に0.0127mm変形することになります。
EXCELでの表計算前記の計算は、あらかじめ最大応力の場所と最大撓みの場所を知っている必要 があります。このため、若干トリック的です。
円板の等分布荷重、周辺固定における計算式を整理すると下記のようになります。
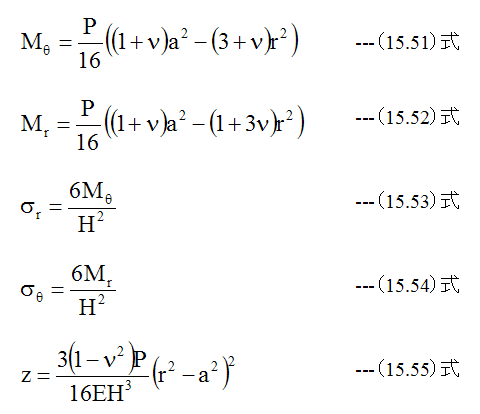
（15.51）から（15.55）式を用いたEXCELでの表計算結果を下記表に示します。
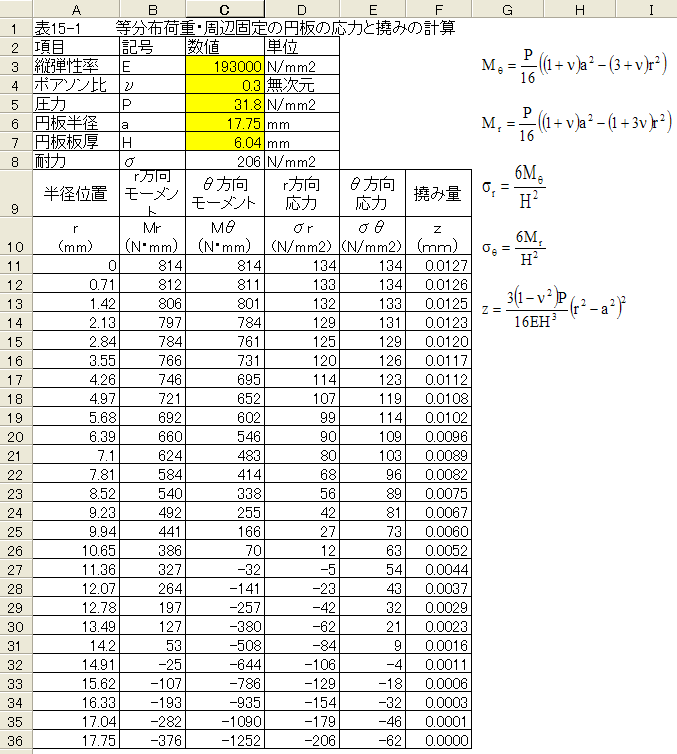
上記の表からわかるように最大応力はｒ方向応力のｒ＝17.75mmで-206N/mm2となり 最大値となります。
また撓み量はr=0mmで0.0127mmの最大値となります。
ワークブック「円板撓み.xls」のダウンロード下記のワークブック「円板撓み.xls」をダウンロードできます。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「円板撓み.xls」をダウンロードする。１５章：円板の軸対称曲げまとめ円板の軸対称曲げの計算は、弾性平行円板ガイド機構の最適化検討で使用しました。
この時は、基礎方程式の誘導の過程は読み飛ばして、計算結果のみをもとめました。
円板の軸対称曲げは基本的に代数解を求めることができます。しかし、モデル条件が異なる と境界条件が異なってきます。積分定数決定のための式の展開は意外と面倒です。
面倒な式の展開をさけるため、当時は数値計算法を活用し単純な手順で解を求めました。
数値計算法での欠点はｒ＝0が特異点で、ｒ＝0で計算エラーが発生する点です。このため、ｒの 値に有限の微小値を設定する必要が生じます。
代数解では、ｒ＝0での矛盾を回避できます。
１６章：コイルバネの話に行く。