コイルバネは標準的な機械要素部品で、頻繁に用いられます。このため、どの機械設計 便覧にもコイルバネの設計方法が記載されています。
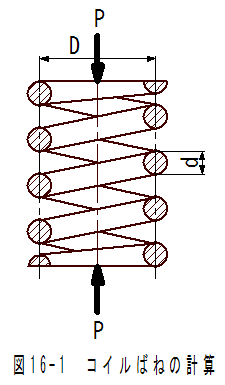
コイルバネの撓みδとばね定数ｋ図16-1にコイルばね計算の説明図を示します。
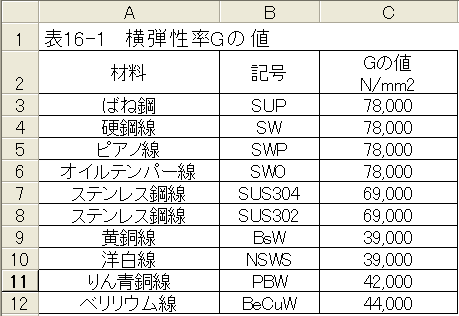
・横弾性係数 G （N/mm2)
・有効巻き数 Na （無次元）
・コイル平均径 D （mm)
・素線径 d (mm)
・ばねにかかる荷重 P （N)
・ばねの撓み δ (mm)
とした場合、下記の公式が一般的に有名です。
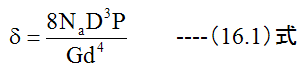
ばね定数ｋは
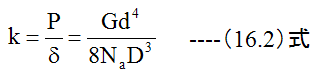
となります。（16.2）式を変形すると
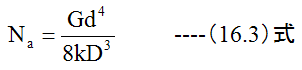
となります。
コイルバネのねじり応力τコイルバネのねじり応力τは下記の公式が一般的に有名です。
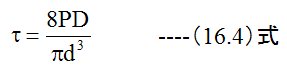
機械工学便覧には、ねじりの修正応力として、ワールの修正式が記載してあります。
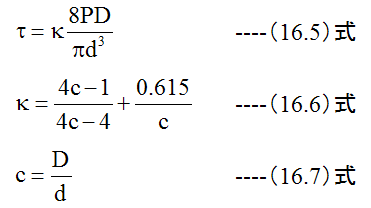
（16.1）式、 （16.4）式は、コイルバネにかかる応力が純粋にねじり応力のみであることを 前提に誘導された理論式です。
しかし実際は、コイルバネには複雑な応力が発生すると思われます。 （16.5）式〜 （16.7）式は 実際のコイルバネに生じる応力を実験的に補正した式と思われます。
横弾性率の値横弾性率の値を下記表に示します。
許容ねじり応力の値主要材料の許容ねじり応力の値を下記のグラフに示します。
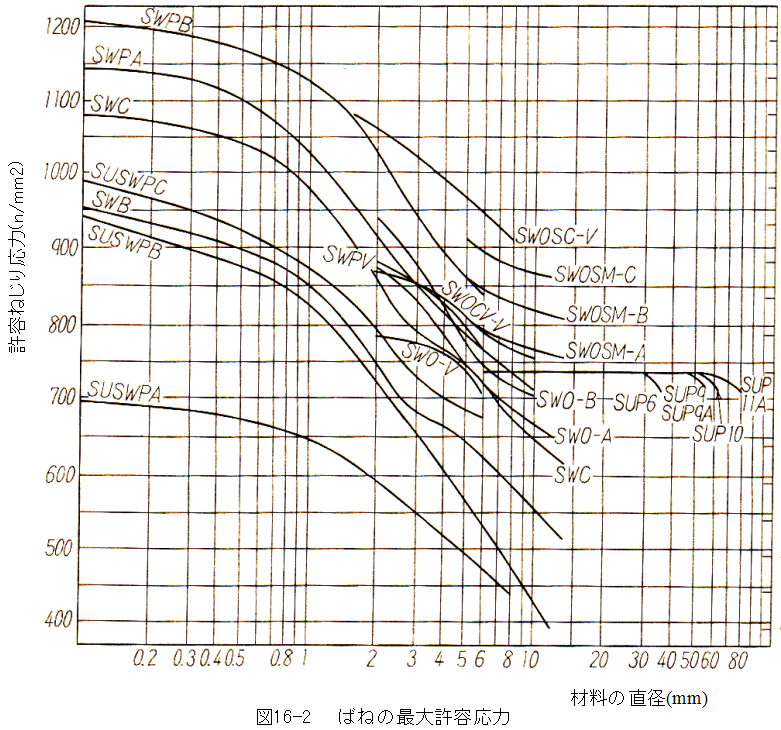
図16-2において、よくばねに使用される材料として、SWPAとSUSWPBがあります。ともに同じ材料 であるにもかかわらず、材料の直径により許容ねじり応力が変化します。
これは、材料の強度が冷間圧延加工による加工歪によって強度が増すことに依存しています。しかし、 加工歪の状態はバラツキが生じることが多く、またばねに加工する際の加工歪や加工後の熱処理にも バラツキが生じることが予想されます。
さらには、短期間の静的な荷重と長期間の変動荷重では、必要な強度が変化します。特に長期間の 疲労破壊に関しては不明確です。
以上の不確定性を考慮すると、安全率を2以上となるような最大応力で使用すべきでしょう。
コイルバネの計算事例丸線コイルスプリング 外径基準ステンレスタイプ （ミスミ）を例にとって、 コイルバネの計算を行ってみます。
型式はUFタイプとします。カタログからは
・横弾性係数G(N/mm2)
・ばね定数k(N/mm2)
・ばね外形(mm)
・素線径d(mm)
・密着長(mm）
・撓みδmax(mm)
を知ることができます。
まず第1に上記の値から、総巻数と有効巻数を計算します。ここで、一般的に「総巻数＞有効巻数」の関係 が成立します。これは、ばねの末端がばねとして有効に作用しないためです。
第2に最大荷重Pと最大応力τを計算します。この結果は、「図16-2 ばねの最大許容応力」に 示す値に対して0.5以下が望ましいです。これは安全率2を確保するためです。（安全率の値の決定は かなり、どんぶり勘定です。）
計算結果を表16-2に示します。
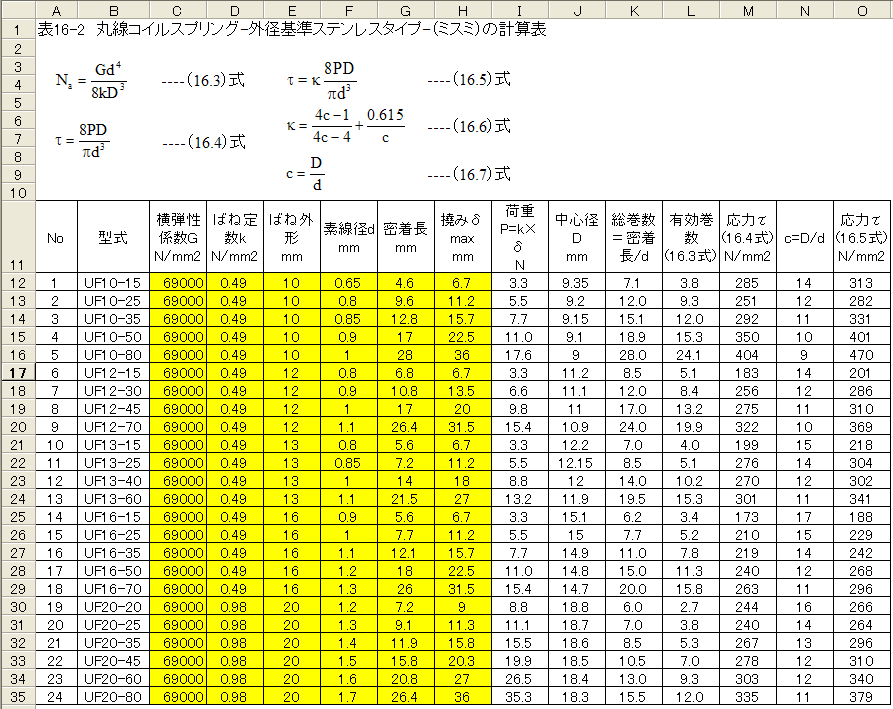
表16-2において、
（１）「総巻数-有効巻数」の平均値は約3.4となっています。これは、コイルの末端において、コイルが密着し ていることを意味しています。
（２）（16.4）式による応力は最小173N/mm2、最大404N/mm2とかなりばらついています。SUSWPBの Φ1mmでの許容応力を825N/mm2とするならば、最大404N/mm2での安全率は2.04ということになります。
（３） （16.5）式による応力は最大470N/mm2です。同様に安全率を計算すると1.75となります。
（４）応力計算においては、 （16.4）式の方が単純で扱いやすくなります。いずれにしても安全率とい う曖昧な係数を使用します。従って、 （16.4）式で安全率2以上で設計すれば、問題は無いと思われます。
ワークブック「コイルばね.xls」のダウンロード下記のワークブック「コイルばね.xls」をダウンロードできます。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「コイルばね.xls」をダウンロードする。
１７章：座屈の話に行く。