断面積に対して長さの大きい柱が圧縮荷重を受けたときに曲げによって破壊が生じる場合があり、 これを座屈といいます。
機械工学便覧には「ランキンの公式」と「オイラーの理論公式」と「テトマイヤーの公式」が紹介されています。これらの 公式について比較検討してみたいと思います。
座屈荷重と座屈応力座屈荷重（Ｐｃｒ）と座屈応力（σcr）の関係は
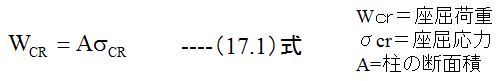
最小断面2次半径（ｋ）最小断面2次半径（ｋ）の定義式は
柱の断面が幅B厚さHの長方形断面の場合
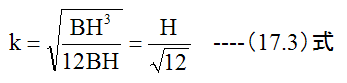
となります。
長柱の細長さ比（λ）長柱の細長さ比（λ）の定義式は
オイラーの理論公式式の誘導は省略しますが、純粋に曲げの基礎方程式から誘導されます。
（17.5）式において端末条件係数は図17-1に示すとおりになります。
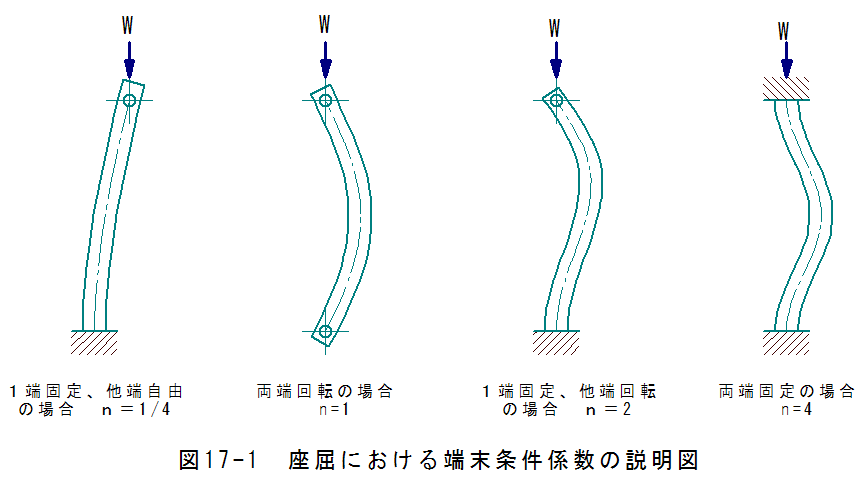
オイラーの理論公式による計算事例板厚1mmのSUS304板材の座屈について具体的に検討して見たいと思います。
SUS304の特性は
・縦弾性率 E=193000 （N/mm2）
・SUS304耐力 σ＝206 （N/mm2）
です。
ここで
・端末条件係数は n=1とします。
（17.5）式に縦弾性率 E=193000 （N/mm2）を代入して長柱の細長さ比（ λ ）と座屈応力 （σcr）の関係をグラフにすると下記の図のようになります。
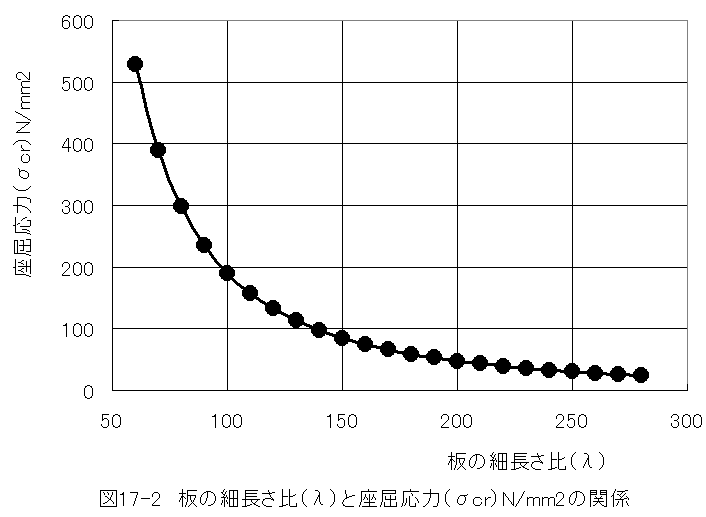
図17-2において、注目すべき点は長柱の細長さ比（ λ ）の値が約100以下になるとSUS304耐力 σ＝206 （N/mm2）を越えてしまう点です。
これは、座屈ではなく圧縮破壊を起こすことを意味しています。オイラーの理論公式は曲げの基礎方程式 から導いており、圧縮応力を無視しています。
長柱の細長さ比（ λ ）の値が約100よりも十分大きい場合、曲げによる座屈が起こります。従って、 オイラーの理論公式は長柱の細長さ比（ λ ）の値が約100よりも十分大きい場合に適用できます。
長柱の細長さ比（ λ ）の値が約100近傍、あるいは小さい場合にはオイラーの理論公式を適用 できなくなり、 「ランキンの公式」、「テトマイヤーの公式」等の実験式を適用する必要性が生じます。
板厚（H)と長柱の細長さ比（λ）の関係式 下記の式から容易に関係式が求まります。
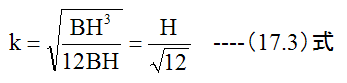
板厚 H=1mmとした場合
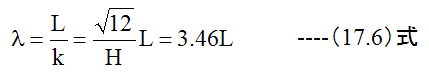
となります。
板厚（H=1mm)の長さ（L)と座屈応力（σcr）の関係 SUS304の特性は
・縦弾性率 E=193000 （N/mm2）
・SUS304耐力 σ＝206 （N/mm2）
です。
ここで
・端末条件係数は n=1とします。
板厚（H=1mm)の長さ（L)と座屈応力（σcr）の関係をグラフにすると下記の図のようになります。
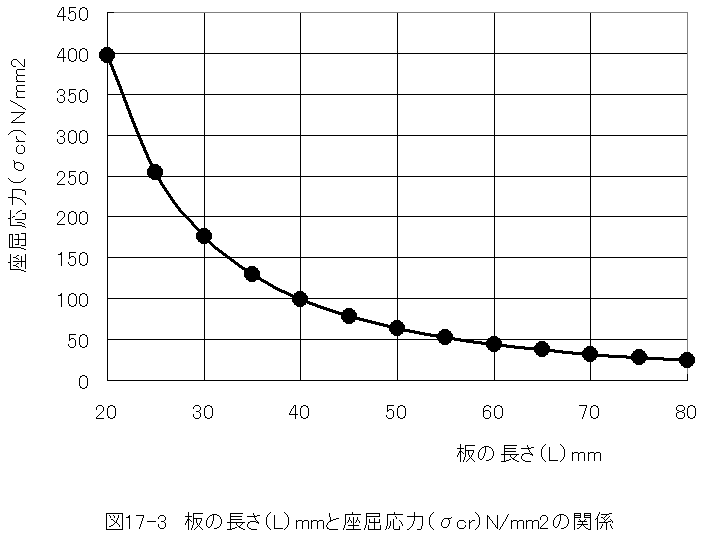
図17-3から厚さ1mmのSUS304板においては、板の長さが約30mmでSUS304の耐力に達することがわかります。
板の長さが約30mmより十分大きいとき、オイラーの理論公式が適用できます。板の長さが約30mm近傍または小さいとき、 「ランキンの公式」、 「テトマイヤーの公式」等の実験式を適用する必要性が生じます。
ランキン（Rankine)の公式
テトマイヤー（Tetmajer)の公式
ジョンソン（Johnson)の公式
ジョンソン（Johnson)の公式はσｙ＞ σｃｒ＞ σｙ/2の間で適用される。また、 σｃｒ＝ σｙ/2で オイラーの理論公式に接するので放物線公式とも呼ばれる。
各公式の比較板厚1mm（SUS304）の座屈応力を各公式で比較してみたいと思います。 SUS304の特性は
・縦弾性率 E=193000 （N/mm2）
・SUS304耐力 σ＝206 （N/mm2）
です。
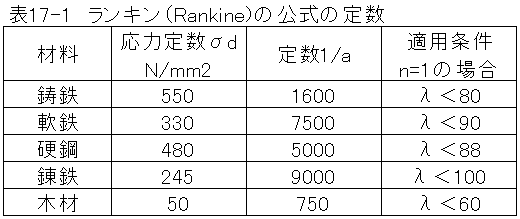
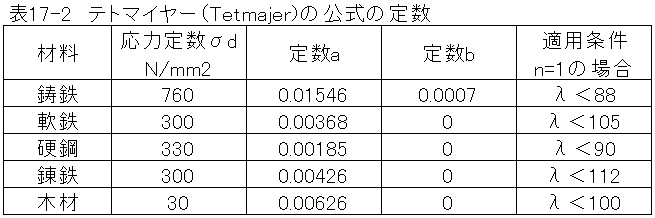
・ランキン（Rankine)の公式とテトマイヤー（Tetmajer)の公式については定数の値が明確にはわかり ません。とりあえず硬鋼の定数で代用します。
・ジョンソン（Johnson)の公式では、 SUS304耐力＝圧縮降伏点応力とします。
各種公式の座屈応力の計算結果比較を図17-4に示します。
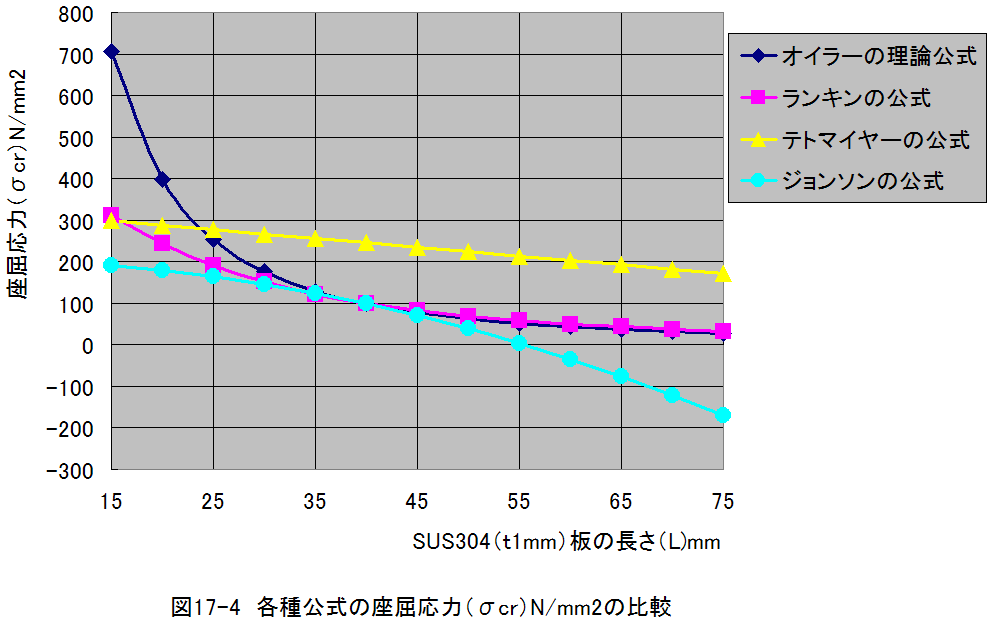
図17-4において、ランキン（Rankine)の公式とテトマイヤー（Tetmajer)の公式についてはSUS304の正確 な定数がわからないという問題があります。
ジョンソン（Johnson)の公式では、 SUS304耐力＝圧縮降伏点応力と考えることができます。
以上の比較結果から判断するに、長さ40mm以下（ σｃｒ＞ σｙ/2）においては、ジョンソン（Johnson)の公式 を適用すべきと思われます。
また、長さ40mm以上（ σｃｒ＜ σｙ/2）においては、オイラーの理論公式を適用すべきと思われます。
座屈まとめ座屈の理論は難解で理解しにくいものがあります。それは、オイラーの理論公式が適用できない範囲 があり、その対応が不明確なためです。
オイラーの理論公式の欠点を補う公式として有効な公式はジョンソン（Johnson)の公式です。この２つの 公式を使い分けることにより、実用的な座屈応力を求めることができます。
ワークブック「座屈.xls」のダウンロード下記のワークブック「座屈.xls」をダウンロードできます。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「座屈.xls」をダウンロードする。
１８章：鉄鋼と熱処理の話に行く。