小型の太陽電池は古くからありましたが、今後は電力の安定供給源としてますます重要となるでしょう。実用化の課 題はコストと発電効率、そして蓄電池との組み合わせによる電力の安定供給となるでしょう。
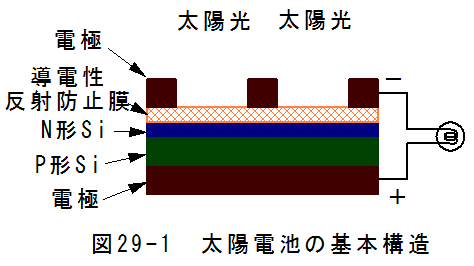
太陽電池の構造図29-1に太陽電池の基本構造を示します。
図29-1において、下側に電極があり、この上にP形シリコン、N形シリコン、導電性反射防止膜の順に積層されています。
導電性反射防止膜の上には格子状の電極が形成されます。
格子状の電極の間から、太陽光は導電性反射防止膜と、N形シリコンを透過し、 P形シリコンとN形シリコンの間の領域まで到達します。
P形シリコンとN形シリコンの間の領域で電子が励起され、自由電子と正孔を生じます。発生した自由電子と正孔は電流となって流れだし 、ランプを点燈します。
シリコンの電子配置太陽電池の原理を理解するには、シリコンの物性を理解する必要があります。
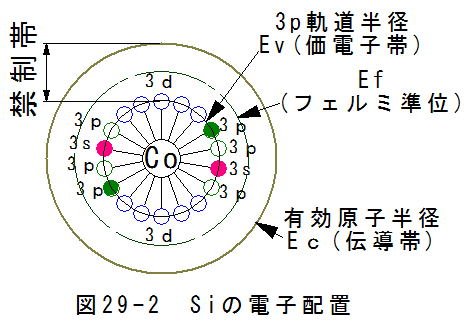
図29-2にシリコンの電子配置を示します。
図29-2において、軌道3sに2個の電子があり、軌道3ｐに2個の電子があります。また軌道3pには4個の空席があります。
さらには、軌道3dには10個の空席があります。軌道3dの空席は空席のままで安定状態となるため、特性にあまり影響しません。
シリコンは軌道3pの4個の空席を埋めようとする作用が働きます。
このため、シリコンは4個の共有結合で安定状態となります。
このため、シリコンはエネルギーの存在しない絶対零度において、絶縁体となります。
常温においては、熱エネルギーが加わるため、一部の電子が軌道3pから抜け出し、有効原子半径の外に飛び出します。このとき、飛び 出した電子は自由電子となり、軌道3pに生じた空席は正孔となります。
言葉の定義の問題なのですが、半導体物理では、軌道3pのポテンシャルを荷電子帯（Ev）といいます。有効原子半径のポテンシャルを伝 導帯(Ec)といいます。伝導帯(Ec)と荷電子帯（Ev）の間を禁制帯といいシリコンでの禁制帯エネルギーが約1.2eVです。 また、エネルギーゼロの基準ポテンシャルをフェルミ準位(Ef)といいます。
真性半導体において、フェルミ準位(Ef)は荷電子帯（Ev）と伝導帯(Ec)の中点となります。
熱エネルギーによる自由電子の発生確率熱エネルギーによる自由電子の発生確率はフェルミーディラックの分布関数から容易に計算できます。
真性半導体の0℃、50℃、100℃における、自由電子の発生確率計算結果を図29-3に示します。
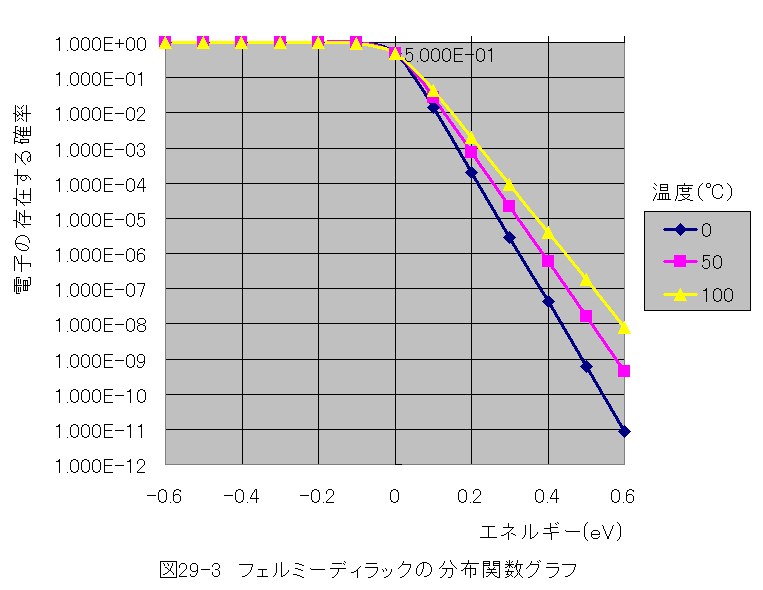
図29-3において、-0.6〜0.6eVの領域は禁制帯の幅であり、自由電子となるためには、0.6eV以上のエネルギーが必要です。
図29-3からわかるように、常温（0〜50℃）にいて、 0.6eVにおける電子の存在確率は1E-10程度の極微量であることがわかります。
また、図29-3において、エネルギーゼロはフェルミ準位と一致させています。図からはわかりにくのですが、このときの確率は全て0.5となります。
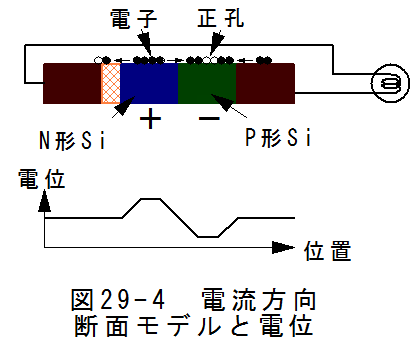
太陽電池の電流方向断面モデルと電位図29-4に太陽電池の電流方向断面モデルと電位を示します。
シリコンにリン等の５価の元素をドープすると、電子があまって自由電子となります。これをN形シリコンといいます。また、ボロン等3価の 元素をドープすると電子が不足して正孔となります。これをP形シリコンといいます。
N形シリコンをP形シリコンと接合しますと自由電子がN形シリコン側からP形シリコン側に流動します。
このため、 N形シリコンはプラスに帯電し、 P形シリコンはマイナスに帯電します。
同様にN形シリコンを導体（金属）と接合すると自由電子がN形シリコン側から導体（金属）に流動します。
同様に 同様にP形シリコンを導体（金属）と接合すると自由電子が導体（金属）からN形シリコン側に流動します。
電子の流動により、電荷分布が発生し、、電荷分布による電位分布が生じます。電子の移動は接合時のみに生じますが、電位分布とバランス して、すぐに電流はなくなります。
したがって、太陽電池の電流方向断面は電流のない安定状態において、電位分布が生じることになります。
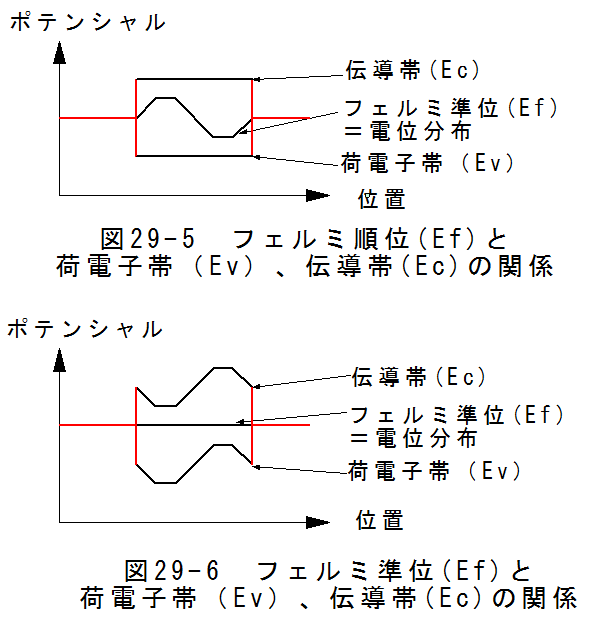
電位分布とフェルミ準位(Ef)、荷電子帯（Ev）、伝導帯(Ec)の関係図29-4に示すように電位分布が生じるとフェルミ準位(Ef)、荷電子帯（Ev）、伝導帯(Ec)の相対関係に変化が生じます。
フェルミ準位(Ef)は、エネルギーゼロの基準ポテンシャルとして定義されます。電流の無い安定状態において、
フェルミ順位(Ef)＝電位分布
となります。
この関係を図29-5と図29-6に示します。
図25-5は、荷電子帯（Ev）、伝導帯(Ec)を一定として、電位分布とフェルミ準位(Ef)が変化するように描いています。
これに対して、図29-6は、電位分布とフェルミ準位(Ef)を一定として荷電子帯（Ev）、伝導帯(Ec)が変化するように描いています。
図25-5と図29-6も相対的な関係は同じなのですが、太陽電池の動作原理を説明する上で図29-6が適しています。
エネルギーゼロの基準ポテンシャルであるフェルミ準位(Ef)を一定として表現したほうが理解がやさしくなります。
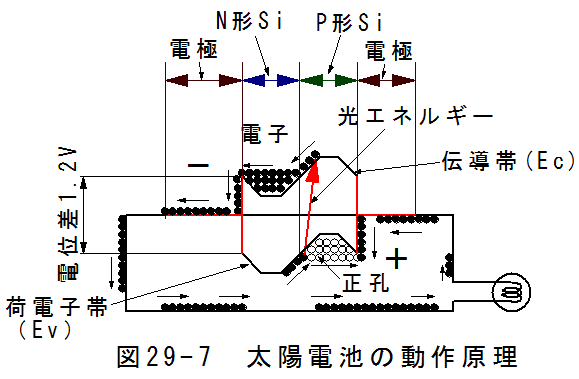
太陽電池の動作原理やっと太陽電池の動作原理の説明です。図29-7に太陽電池の動作原理説明図を示します。
図29-7は、目に見えないエネルギー状態をモデル的に書いたものです。電位は相対的な量であり、電流が流れない時の電位をゼロとし、伝 導体(Ec)と荷電子帯(Ev)の相対的な電位を示しています。
また、図29-7においては、マイナスに帯電すると上側に変化し、プラスに帯電すると下側に変化することに注意が必要です。
N形シリコンとP形シリコンの境界部において、荷電子帯にある電子に光エネルギーが加わると電子はエネルギーを得て、伝導帯にジャンプします。
ジャンプした電子は伝導帯の山の頂上付近に着地することになります。電子は山の斜面にそってマイナス側電極に流れ込みます。
一方、電子が飛び出した荷電子帯は電子が不足するため、正孔となります。発生した正孔はプラス側電極に向かって流れだします。
マイナス側電極に流れだした電子はランプを点燈し、プラス側電極まで流れます。プラス側電極では正孔と電子が合流し消滅します。
金属製の導線は、電位を保持したまま伝達するパイプのような役目をします。ランプでの電圧降下を無視した場合、N形シリコンの伝導帯の電位 とP形シリコンの荷電子帯の電位の差（約1.2V)の電圧が発生することになります。
以上が太陽電池の動作原理ですが、納得できない方も多いと思います。
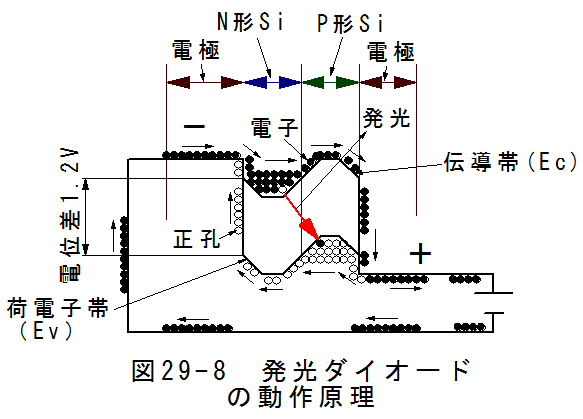
発光ダイオードの動作原理太陽電池に電圧をかけると発光ダイオードとして動作します。
図29-8は太陽電池に1.2V以上の電圧をかけた場合のエネルギー状態図を示します。この場合、電気の流れる経路は3通りとなります。
第1は電子の流れです。電子は電池のマイナス側から流れだし、伝導帯を経由して、電池のプラス側まで流れます。
第2は、正孔の流れです。正孔は電極とP形シリコンの境界で発生し、N形シリコンと電極の境界までながれます。
第3はN形シリコンとP形シリコンの境界部で伝導帯の電子が直接荷電子帯の正孔と合流して消滅する流れです。
第3の流れは大きなエネルギーの消滅を伴いますがこのとき発光します。これが発光ダイオードの基本原理です。
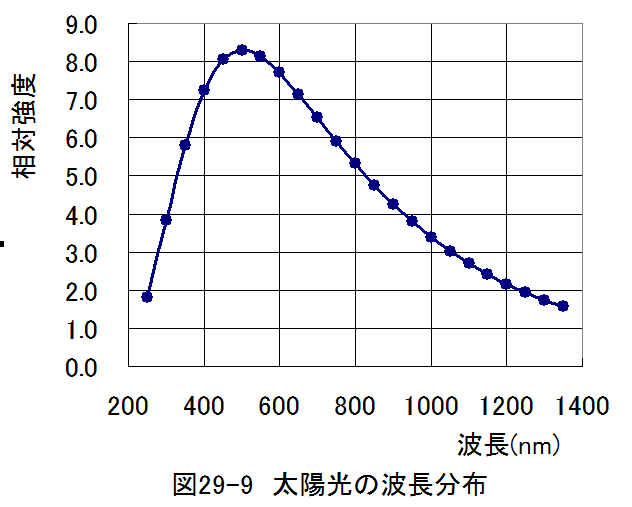
太陽光の波長分布太陽の表面温度は5778°Kです。波長分布はプランクが提唱した黒体放射の式から容易に計算できます。計算結果を図29-9に示します。
図29-9からわかるように相対強度が最大となるのは、波長が約500nmとなります。シリコン太陽電池では、全ての波長が有効となるわけではありません。
波長が1000nm以上の赤外腺は光子エネルギーが小さいため、電子を荷電子帯から伝導帯まで励起できません。
逆に波長が短いと光が表面で吸収され、PN接合部まで、光が到達できなくなります。
光子エネルギー光のエネルギーは、連続量ではなく、離散的な量となります。この光の離散量の最小単位を光子といいます。
光子のエネルギー（E)は下記式で定義されます。
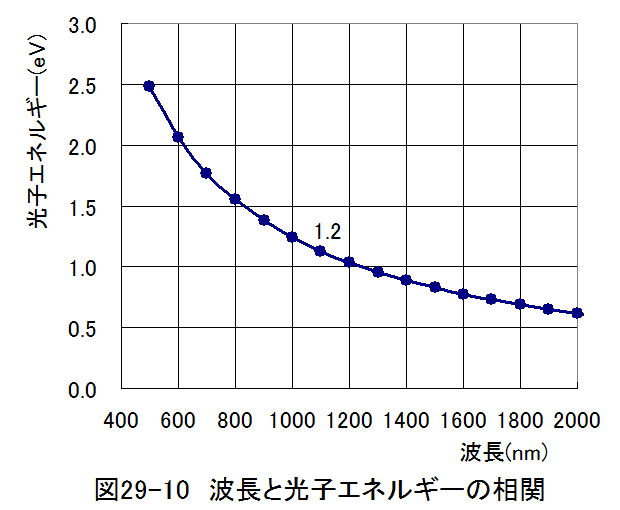
E=hν＝ｈｃ/λ
ｈはプランク定数、νは光の振動数、ｃは光速、λは光の波長です。具体的な計算結果を図29-10に示します。
図29-10からわかるように光子のエネルギー（E)が1.2eVとなるのは波長1000nmであり近赤外腺となります。
このため、シリコンの発光ダイオードは、波長1000nmの近赤外腺となります。波長1000nmの近赤外腺は肉眼では検知できません。このため、 照明用としては使えません。主にリモコン等の赤外腺通信に用いられます。
シリコン薄膜の透過率シリコン薄膜の透過率を計算するのは、各波長における複素屈折率の測定値が必要となります。
表29-1にシリコンの複素屈折率を示します。
表29-1 シリコンの複素屈折率
| N実測値 | K実測値 | |
| 300.9 | 5.02 | 3.979 |
| 350.2 | 5.442 | 2.989 |
| 400 | 5.57 | 0.387 |
| 449.2 | 4.682 | 0.149 |
| 499.9 | 4.298 | 0.073 |
| 548.6 | 4.089 | 0.044 |
| 601.9 | 3.943 | 0.025 |
| 645.8 | 3.858 | 0.017 |
| 696.5 | 3.787 | 0.013 |
| 746.9 | 3.736 | 0.009 |
| 805.1 | 3.688 | 0.006 |
| 826.6 | 3.673 | 0.005 |
| 1120 | 3.536 | 0 |
表29-1から、膜厚250nm、500nm、1000nmのシリコン薄膜の透過率を計算した結果を図29-11に示します。
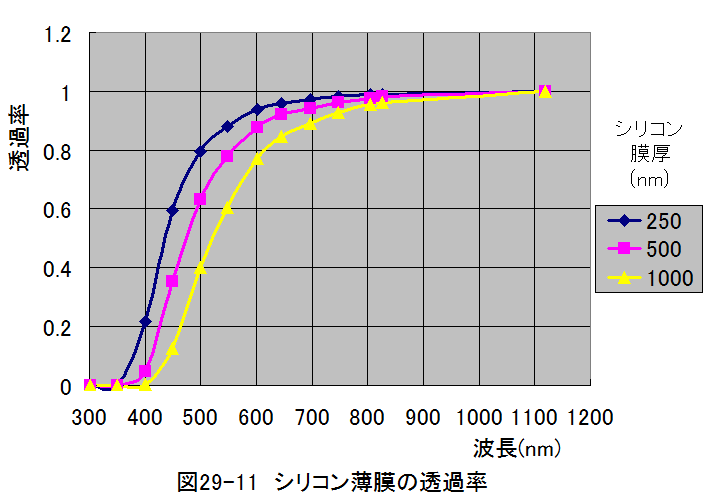
図29-10から波長500nm以下で透過率が急激に低下することがわかります。
太陽電池まとめ太陽電池は今後の電力供給になくてはならないものになるでしょう！！課題はコストと発電効率です。
３０章：燃焼によるエネルギーに行く。