粘性流体の理論は難しくて、あまり自信がありませんが、大まかな検討をしてみたいと思います。
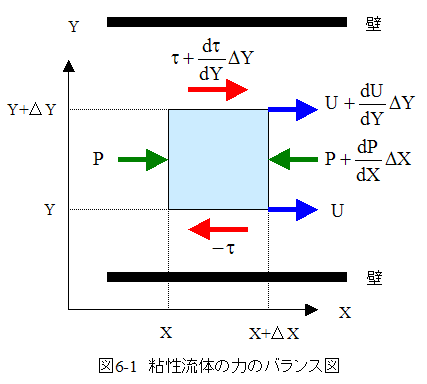
２平板間流れの基礎方程式粘度の定義式を微分形で表現すると ・せん断応力＝τ
・粘度＝μ
・速度変化量＝ｄU
・厚さ変化量＝ｄY
として
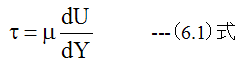
図6-1に粘性流体の力のバランス図を示します。
図6-1において、流体の流れはX方向とします。また流れの方向を決める壁はX軸とZ軸に平行とします。
このような条件において、流速Uの変化はY軸方向のみに発生します。また、圧力Pの変化はX軸の方向に生じます。
ここで、微小立方体ΔXΔYΔZに加わる力のバランスを考えます。
微小立方体の底面と上面のせん断応力の変化Δτは
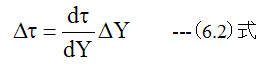
微小立方体の底面と上面流速の変化ΔUは
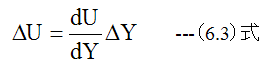
τ＝Δτ、U=ΔUと置き換えて、 （6.1）式に（6.2）式と（6.3）式に代入します。
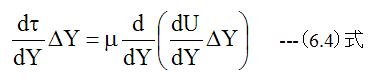
すなわち
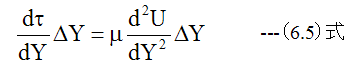
（6.5）式に微小立方体の上面の面積ΔXΔZをかけるとX方向の力が求まります。
微小立方体の左側と右側の圧力変化ΔPは
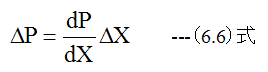
（6.6）式に微小立方体の右側の面積ΔYΔZをかけるとX方向の力が求まります。
力のバランスから（6.5）式にΔXΔZをかけた値と（6.6）式のΔYΔZをかけた値は等しくなります。
従って
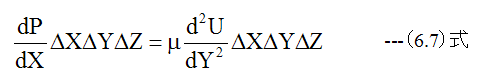
すなわち
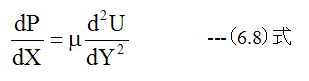
となる。
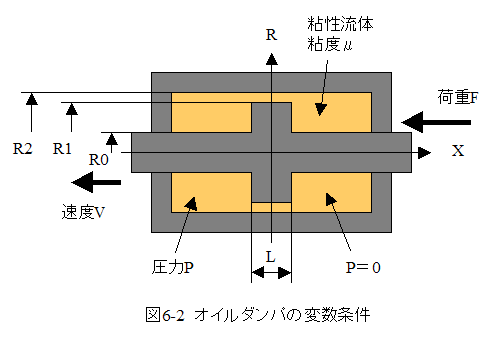
オイルダンパの粘性抵抗を求める式図6-2にオイルダンパの変数条件を示します。
図6-2に示すオイルダンパに右側から荷重Fを加えると左側に圧力Pが発生します。圧力Pにより粘性流体は半径R2とR1の隙間を流動し右側に移動します。これにより、左側の粘性流体が減少し右側が増大するため、ピストンは速度Vで移動します。
ここで
とします。 （6.8）式に（6.12）式を代入すると
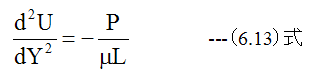
となります。 （6.13）式の解は、C1、C2を積分定数として
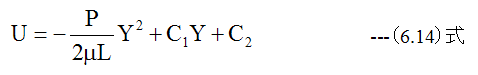
となります。ここで、Y=0とY=Hにおいて、粘性流体の流速Uはゼロでる条件を入れて積分定数C1とC2を求めます。
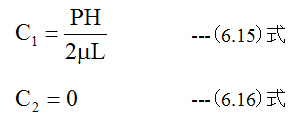
したがって
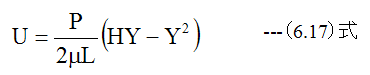
となります。隙間Hを通過する粘性流体の流量Qは
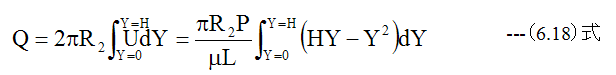
（6.18）式の積分を実行すると
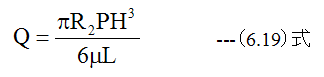
となります。 （6.19）式は粘度μ、半径R、長さL、圧力Pに関しては1次の関係がありますが、隙間Hに関しては3乗の関係があることがわかります。
隙間Hを変化すると流量Qは急激に変化します。
図6-2のオイルダンパの変数条件において荷重Fと速度Vの関係式は
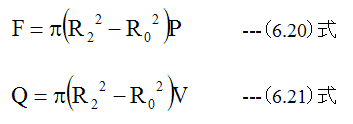
となります。オイルダンパの粘性抵抗Cは
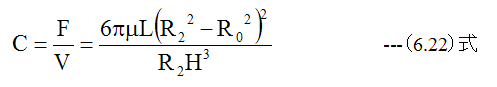
となります。 （6.22）式において、粘度μと長さLは１次の比例関係が成立することがわかります。
オイルダンパの粘性抵抗計算例計算条件
・シャフト半径：R0＝2(mm)
・シリンダ内半径：R2=5(mm)
・隙間幅：L=4(mm)
・粘度：μ=100(mPa・s)
・隙間：H＝0.01から0.4 (mm)
として、オイルダンパの粘性抵抗を計算します。
また、推力F＝50Nとして、速度Vを計算します。
計算結果グラフを図6-3に示します。
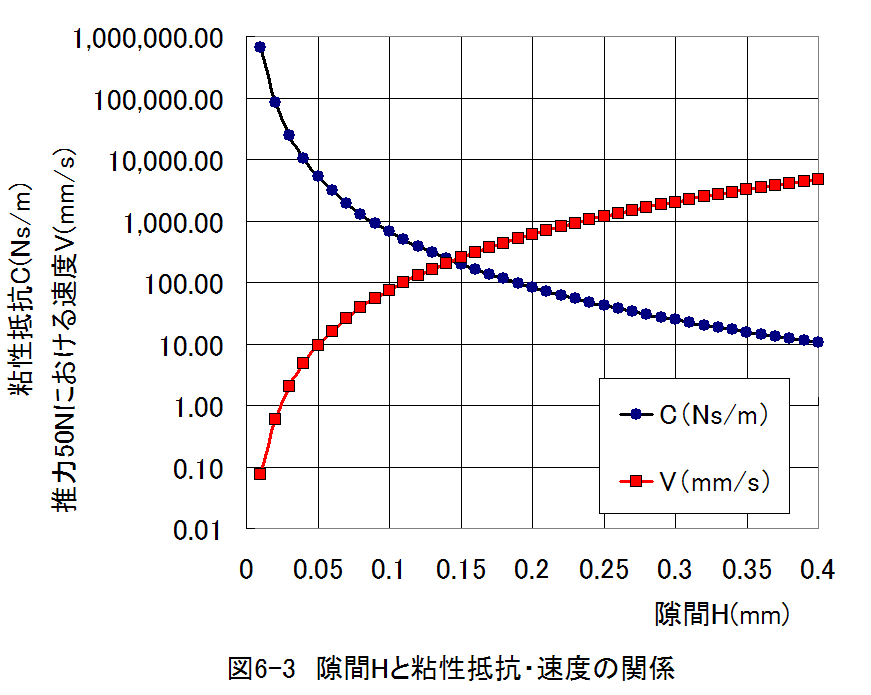
2点間往復運動機構において、推力50Nのエアーシリンダを用いて、速度10mm/sに減速する場合は、シリンダの隙間H=0.05mmに設定すればよいことがわかります。
また、粘性流体の粘度は100ｍPa・ｓとしていますが、1〜数万ｍPa・ｓ程度の範囲で変更可能ですので、シリンダの隙間Hは0.1mm程度が適正と思われます。
なお、以上の結果は理論的検討結果であり、実験的に確認されたものではありません。正確な値は実験的に求める必要があります。
７章：加圧によるレジスト流動に行く。