加圧によるレジスト流動について、大まかな検討をしてみたいと思います。
加圧によるレジスト流動の基礎方程式２平板間流れの基礎方程式は
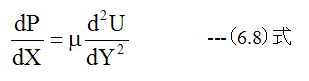
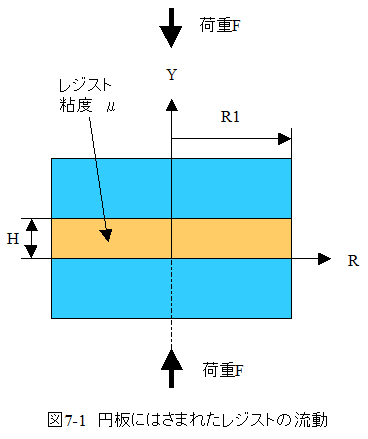
で与えられますが、変数を図7-1に示す条件に変更します。ここで
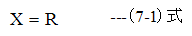
とすると（6.8）式は
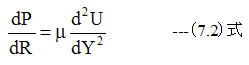
となります。
（7.2）式の解は
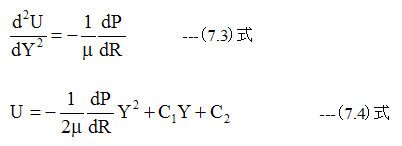
となります。ここで、Y=0とY=Hにおいて、粘性流体の流速Uはゼロである条件を入れて積分定数C1とC2を求めます。
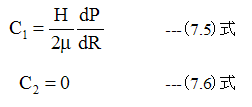
したがって
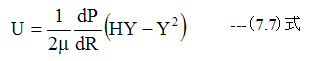
となります。半径Rでの隙間Hを通過する粘性流体の流量Qは
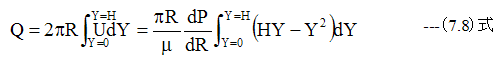
（7.8）式の積分を実行すると
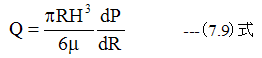
さて、円板の間隔が単位時間にｄHだけ減少したとき 、中心から周辺に向かって流れるレジストの流量は下記式を満足する必要があります。
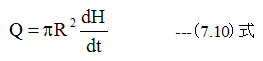
（7.9）式と（7.10）式から
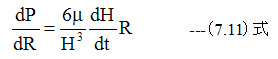
（7.11）式を積分して
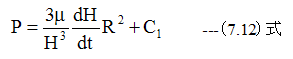
R=R1における圧力P=0とすれば
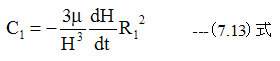
（7.12）式に（7.13）式を代入すると
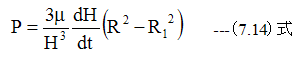
推力Fは圧力Pの積分となります。
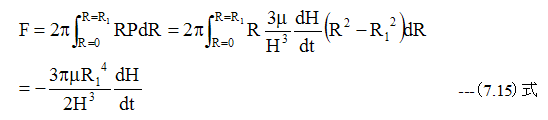
推力Fを一定とした場合のレジスト厚さの変化は
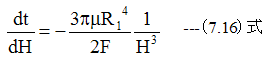
積分すると
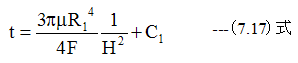
t=0でのレジスト厚をH1とすれば
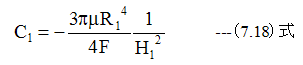
（7.17）式に（7.18）式を代入して
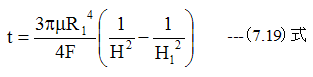
（7.19）式を変形して
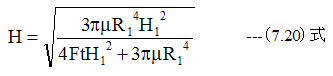
H1=∞とした場合は
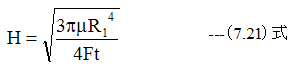
となります。
球面加圧
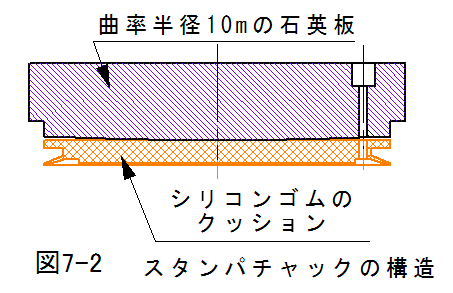
２章：S&Rナノインプリント転写治具の設計において、中心から周辺に向かう圧力勾配をを得る構造 は図7-2に示すような、条件になっています。
曲率半径ρの幾何学条件において下記式が近似的に成立します。
横をX、縦をYとして
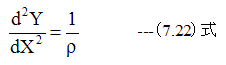
（7.22）式を積分して
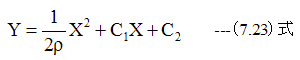
X=0において、Y=0、ｄY/dX=0とするならば、C1=0、C2=0となります。
従って球面は
で近似できることになります。
曲率半径＝10000mmでの近似式による計算誤差を下記表に示します。
| X（ｍｍ） | 球面Y（ｍｍ） | 近似Y（ｍｍ） | 誤差(mm) |
| 0 | 0.0000 | 0.0000 | 0 |
| 5 | 0.0013 | 0.0013 | -7.75617E-11 |
| 10 | 0.0050 | 0.0050 | -1.25066E-09 |
| 15 | 0.0113 | 0.0113 | -6.32783E-09 |
| 20 | 0.0200 | 0.0200 | -2.00002E-08 |
| 25 | 0.0313 | 0.0313 | -4.8829E-08 |
| 30 | 0.0450 | 0.0450 | -1.0125E-07 |
| 35 | 0.0613 | 0.0613 | -1.87578E-07 |
| 40 | 0.0800 | 0.0800 | -3.20002E-07 |
| 45 | 0.1013 | 0.1013 | -5.12584E-07 |
| 50 | 0.1250 | 0.1250 | -7.8126E-07 |
シリコンゴムの縦弾性係数をE、歪をεとした場合の応力Pは
シリコンゴムの厚さをT、変形量をYとした場合、
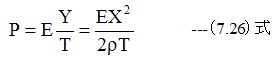
となります。
推力Fは（7.26）式のX=Rとしての積分となります。
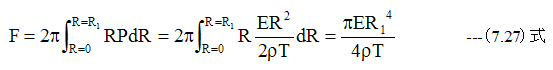
（7.27）式において
・クッションの縦弾性率 E
・クッションの厚さ T
・球面曲率半径 ρ
は1次の関係があり
・転写半径 R1
は4次の関係が成立することがわかります。
これは、推力Fは転写半径 R1の４乗に比例するため、転写面積が増大すると 、急激に必要推力が増大し転写が難しくなることを示しています。
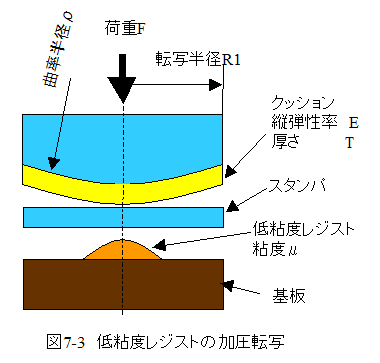
低粘度レジストの加圧転写ナノインプリントにおいて、一番簡単な転写方法を図7-3に示します。
図7-3において、基板上に低粘度レジストを滴下して、スタンパを載せます。
その上にクッションを置き、球面レンズ等で加圧します。
加圧により、低粘度レジストは押し出されます。その後、UV照射によりレジストを硬化します。
そして、スタンパと基板を剥離すればナノインプリントの転写は完了します。
この方法は一見シンプルで、優れた転写方法に思えますが、実際にやってみるとさまざまな問題に遭遇します。
この実験を行うには、まず低粘度のUV硬化性レジストを調合する必要があります。粘度は低いほどよいのですが限界が存在します。 十分なUV硬化特性、硬化物の物性を考慮すると粘度は5mPa・ｓ〜10000 mPa・ｓの範囲となります。 極端な低粘度化は難しいのですが、トライアルで超低粘度な下記のUV硬化性樹脂を調合します。
M0279:E0102:M0720:A0145;H0991=1:1:1:1:06
M0279：粘度2.8mPa・ｓ メタクリル酸ベンジル CAS番号 : 2495-37-6
（耐ドライエッチ性向上のためのおまじない材料、硬化物はゲル状）
E0102 ：粘度3.1mPa・ｓ エチレングリコールジメタクリラート CAS番号 : 97-90-5
（硬化反応は遅い、３次元結合で硬化物は硬い。）
M0720：粘度0.6mPa・ｓ メタクリル酸ビニル CAS番号 : 4245-37-8
（硬化反応は得に遅い、３次元結合で硬化物は硬い。）
A0145 ：粘度0.48mPa・ｓ アクリル酸メチル CAS番号 : 96-33-3
（硬化反応は激しく、反応熱がでる。硬化物はゲル状）
H0991 ：粘度22mPa・ｓ 2-ヒドロキシ-2-メチルプロピオフェノン CAS番号 : 7473-98-5
（光重合開始剤、標準よりかなり多めに配合）
上記の配合で混合粘度は2mPa・ｓ程度になります。非常に揮発性が高く、臭いのきついレジストとなります。 （使用環境と取り扱いに注意すれば、使用量が微量ですのでなんとかなるでしょう。）
いよいよ、実験ですが転写面積、球面の曲率、クッションの厚さを決定する必要があります。
・転写半径 R1=15mm
・球面の曲率 ρ＝1250mm
・クッション縦弾性率 E=40 N/mm2
・クッション厚さ T＝1mm
とします。
この時の必要推力は
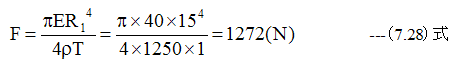
となります。
次に下記式で加圧時間に応じたレジスト膜厚の変化を調べます。レジストの初期膜厚を無限大とします。
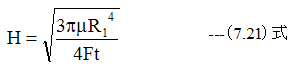
・レジスト粘度 μ＝2mPa・s
・転写半径 R1=15mm
・加圧推力 F＝1272 N
として計算した結果を下記図に示します。
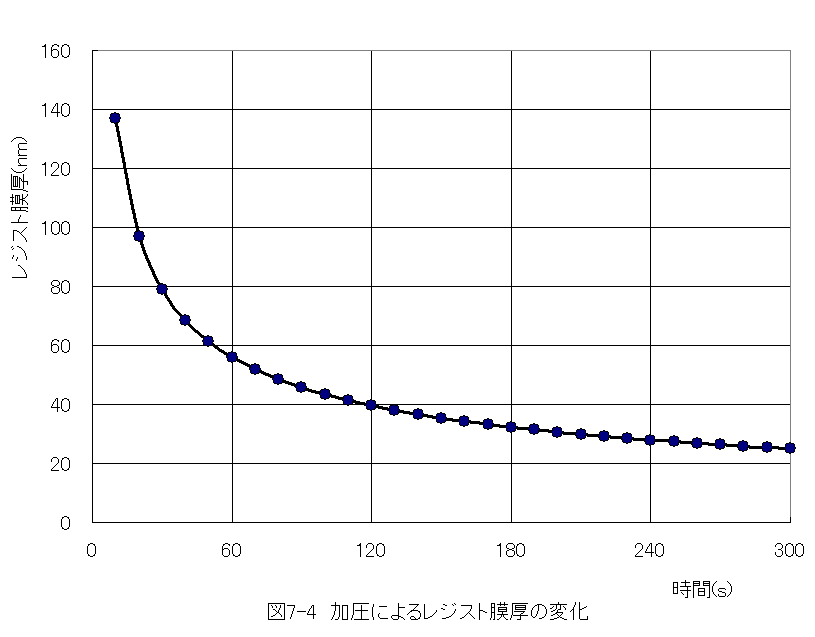
図7-4において、膜厚は0〜60ｓの間に急激に変化することがわかります。60ｓ後にはレジスト膜厚は60nm以下に達します。
もし、スタンパが凸パターンであるならばベース膜厚は十分に小さくなります。転写半径が15mm以下であれば、 この方法でナノインプリントは可能です。
この方法で転写する場合下記の問題点が生じます。
・微小な異物の影響で転写欠陥が発生します。
・転写面積が大きくなると、急激に転写が難しくなります。
・余分なレジストが押し出されるため、ステップ＆リピート転写は困難です。
上記の問題点はリソグラフィー用途としては、致命的な問題点であり実用性に乏しい技術です。
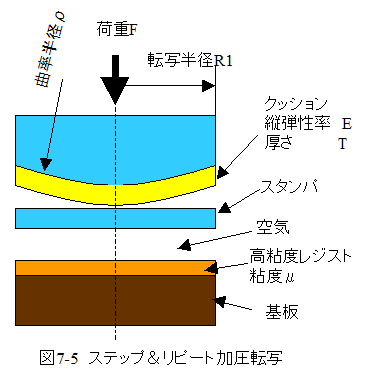
ステップ＆リピート転写における空気の押し出し図7-5にステップ＆リピートにおける加圧転写の原理図を示します。
高粘度レジストはあらかじめ、スピンコート法で基板上に塗布します。
良好な転写を行うには、スタンパと高粘度レジストの間にある空気をすみやかに排出する必要があります。
しかし、均一に塗布したレジストは加圧により、外周部に流出させたくありません。また、 スタンパへのダメージを考慮すると加圧推力をあまり大きくしたくありません。
このような条件から
・転写半径 R1=30mm
・球面の曲率 ρ＝10000mm
・クッション縦弾性率 E=40 N/mm2
・クッション厚さ T＝6mm
とします。
この時の必要推力は
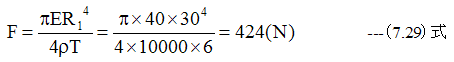
となります。
次に下記式で加圧時間に応じた空気膜厚の変化を調べます。空気トの初期膜厚を無限大とします。
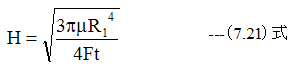
・空気粘度 μ＝0.01869mPa・s
・転写半径 R1=30mm
・加圧推力 F＝424 N
として計算した結果を下記図に示します。
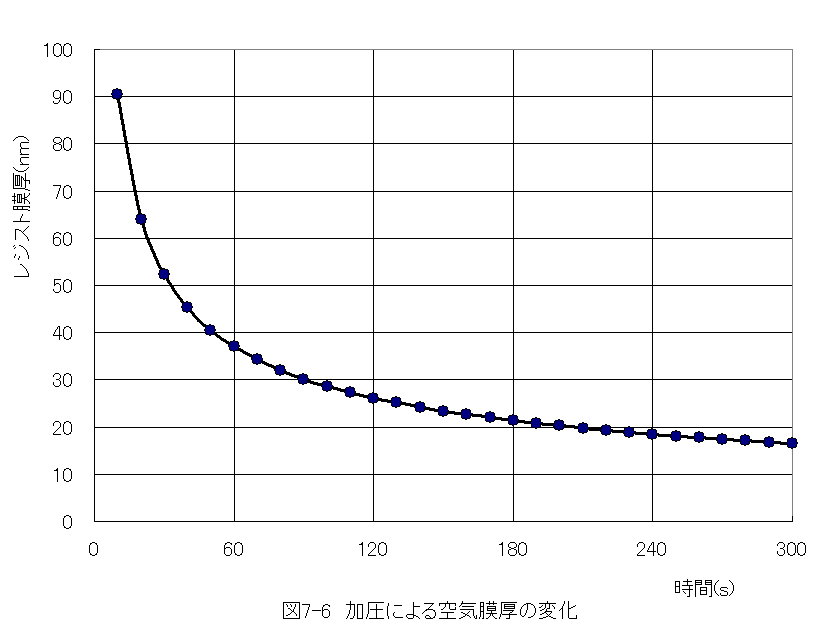
図7-5に示す計算結果によれば、空気の層は60ｓ加圧後において、37nmも残る結果となって います。しかし、この計算結果は、空気が非圧縮性でレジストに溶解しないことを前提としてい ます。実際には、圧縮性でレジストに溶解するため問題ない量になると思われます。
ステップ＆リピート転写における高粘度レジストの流動均一に塗布したレジストは加圧により、外周部に流出させたくありません。しかし、どの程度流動するかは計算し てみる必要があります。
下記式で高粘度レジストの流動を計算します。
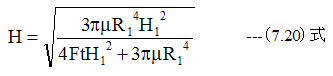
初期膜厚は、2層反転プロセスで厚めに設定する必要が生じます。これは、微小な異物をレジストの厚さで 吸収する必要があるためです。このため、初期膜厚 H1=1000nmで計算します。
・初期膜厚 H1=1000nm
・レジスト粘度 μ＝2000mPa・s
・転写半径 R1=30mm
・加圧推力 F＝424 N
として計算した結果を下記図に示します。
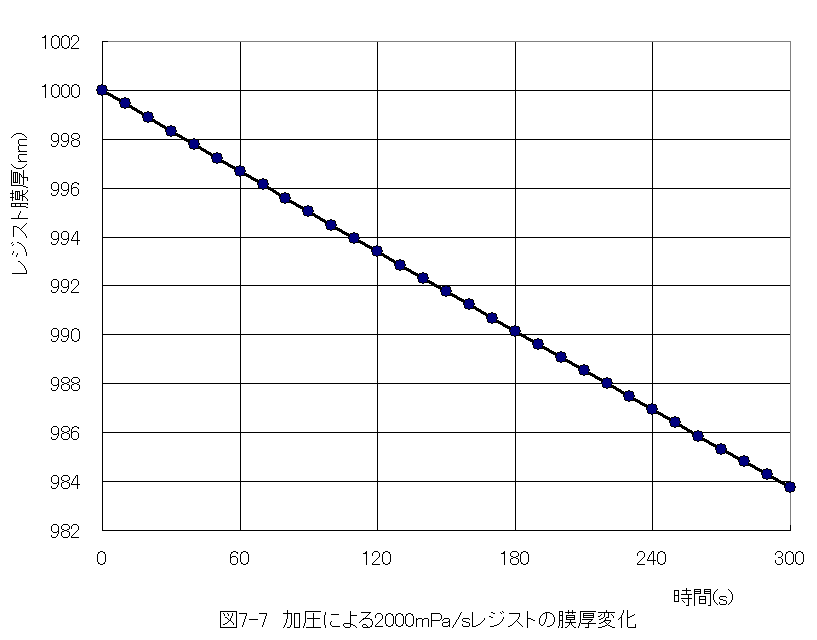
図7-6に示す計算結果によれば、60ｓの加圧において、レジスト膜厚の減少はわずかに3nm程度であり、ほとんど流動しないことがわかります。
思い出加圧による粘性流体の流動に関しては、いろいろと思い出深いものがあります。最初の思い出はコンタクトアライナーのマスクとウエハの密着に関する検討です。この場合は、マスクとウエハ間の空気の押し出しですが、中心から周辺に向かっての加圧が必要なことを理解しました。
ナノインプリントの検討ですが、この場合レジストを押し出すことが必要でした。最初は軽く考え加圧実験を行ったのですが、空気を押し出すようにはいかないことがすぐに確認できました。 転写面積が小さければレジストを十分薄くなるまで加圧することは可能です。しかし、転写面積が大きくなると急激に難しくなります。
使用するレジストの粘度と必要転写面積で異なるのですが、必要とされた面積を転写するための推力を試算すると30ｔという結果がでました。 ただ加圧するだけでしたら、機械設計で30tの推力を得ることはさほど難しくはありません。早速最大推力60ｔの加圧治具を設計し試作しました。
実際に30ｔを越える推力で加圧実験をおこなってみると、予想どおりレジストの残膜厚は薄くなりました。しかし、ガラスやシリコンのような脆性材料に30ｔもの荷重をかけると破壊等が発生しやすく実用とは程遠いものでした。この問題を解決したのはスピンコート法による転写方法です。