固体材料の物性として、弾性率（ヤング率）があります。弾性率（ヤング率）について検討してみたいと思います。
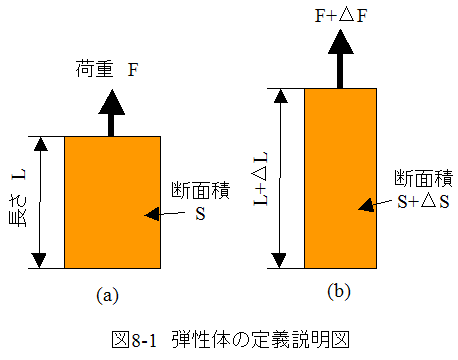
ばね定数図8-1に弾性体の定義説明図を示します。
図8-1において、ばね定数（K）は以下のように定義されます。
ばね定数の定義式（8.1）式または（8.2）式において、関係するのは荷重の変化量ΔFと長さの変化量ΔLのみです。
ばね定数は、初期長さ（L）,初期荷重（F）、初期断面積（S）、断面積変化量（ΔS）は無視して決定されるのが特徴的です。
ばね定数は一般的にコイルバネの特性を表すのに用いられ、単位はN/mmが多く用いられます。
歪歪の増加分（Δε）は以下のように定義されます。
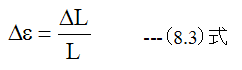
（8.3）式の定義からわかるように、歪（ε）の単位は無次元となります。
応力応力（σ）は以下のように定義されます。
応力の増加分（Δ σ ）は
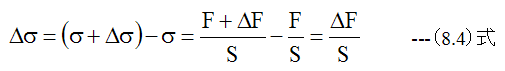
応力（σ）は材料の強度計算で重要なパラメータです。単位はMPaやN/mm2が多く用いられます。
ポアソン比ポアソン比（ν）は断面積の変化に関係するパラメータです。
横方向の歪の増加分（Δε’） は
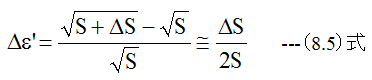
（8.5）式はテーラー級数展開による近似式です。
ポアソン比（ν）は以下のように定義されます。
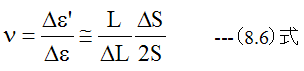
ポアソン比はなじみの薄い項目ですが、鉄鋼では0.28〜0.3の値となり、単位は無次元となります。
縦弾性率（ヤング率）縦弾性率（E)（ヤング率）は以下のように定義されます。
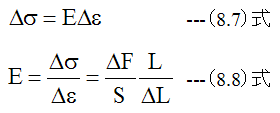
（8.8）式から、縦弾性率（E)（ヤング率）の単位はMPaまたは、N/mm2ということになります。
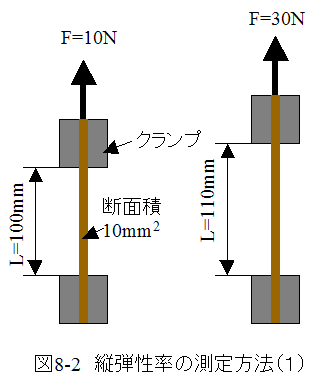
縦弾性率（ヤング率）の測定方法（１）厚さ1mm、幅10mmのシリコンゴムの試験片を作り、図8-2に示すような結果が得られたとします。
この場合の縦弾性率（ヤング率）は以下のように計算できます。
・初期長さ L=100mm
・断面積 S=10mm2
・荷重増加分 ΔF=20N
・長さ増加分 ΔL=10mm
以上の値を（8.8）式に代入すると
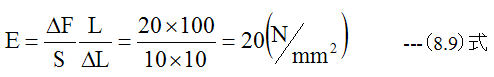
比較的簡単に縦弾性率（ヤング率）を計算できることがわかります。
縦弾性率（ヤング率）の測定方法（２）鉄鋼のような機械材料で図8-2と同じ条件で実験すると長さ増加分ΔLは非常に小さくなります。
長さ増加分ΔL は以下の計算で予測できます。
・初期長さ L=100mm
・断面積 S=10mm2
・荷重増加分 ΔF=20N
・長さ増加分 ΔL=10mm
・縦弾性率 E=210000（N/mm2）
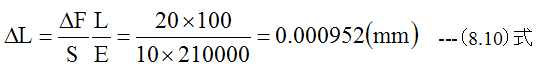
（8.10）式に示すように随分と小さな値となります。従って微小な長さの変化を正確に測定する必要が生じます。
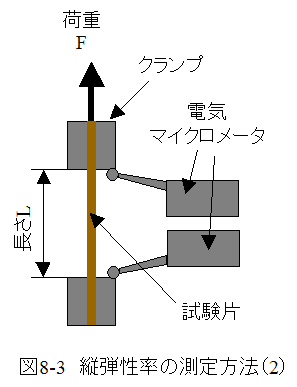
微小な長さの変化を測定する手段としては電気マイクロメータ等があり、約0.1μm程度の変化を読み取ることができます。
試験片の断面積、長さ、荷重等の最適化により鉄鋼のような機械材料の測定も可能です。
縦弾性率（ヤング率）の測定方法（３）精密測定においては、縦弾性率（ヤング率）の測定方法（２）が望ましいのですが、もっと簡単に縦弾性率を測定する方法があります。
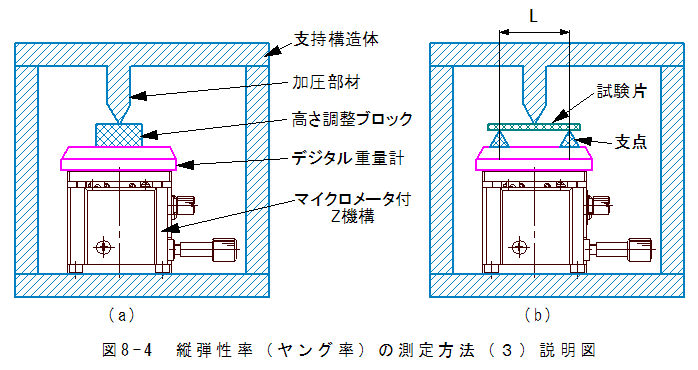
図8-4に縦弾性率（ヤング率）の測定方法（３）の説明図を示します。
測定治具は、マイクロメータ付Z機構、デジタル重量計、支持構造体で構成されます。
- 測定治具のばね定数（K0）の測定
まずは、測定治具のばね定数（K0）の測定を行います。
・荷重変化量 ΔF=5N
・Z変化量 ΔZ=0.5ｍｍ
の場合、測定治具のばね定数（K0）は
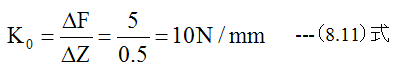
となります。
- 試験片をセットした場合ののばね定数（K1）の測定
次に試験片をセットした場合ののばね定数（K1）の測定を行います。
・荷重変化量 ΔF=5N
・Z変化量 ΔZ=1.5ｍｍ
の場合、試験片をセットした場合ののばね定数（K1）は
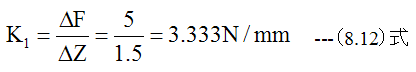
となります。
- 試験片のみのばね定数（K)の算出
試験片のみのばね定数（K)の算出します。
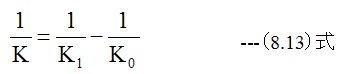
（8.13）式を変形して
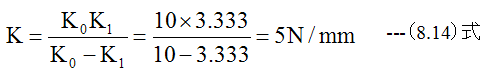
- 試験片の縦弾性率（ヤング率）の計算
単純支持中央集中荷重の撓み量（δ）の公式から
（8.15）式、 （8.16）式変形して
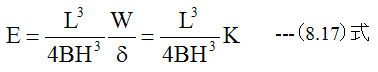
ここで、試験片の具体的な値を（8.17）式に代入します。
・梁の長さ L=50mm
・梁の幅 B=10mm
・梁の厚さ H＝2mm
・ばね定数 K=5N/mm
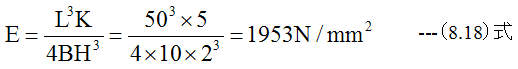
計算結果は、 （8.18）式に示す通り約2GPaとなります。この値は平均的な樹脂の縦弾性率（ヤング率）の値です。
鉄鋼のような機械材料の場合は、試験片の厚さを薄くすることにより、変形量が増して測定しやすくなります。
一般的な機械材料の縦弾性率（ヤング率）は公開されており、測定する必要がないかもしれません。しかし、特殊な樹脂材料を調合した場合は、自分で測定する必要が生じます。こんなとき、縦弾性率（ヤング率）の測定方法（３）は手軽な測定方法です。
9章：梁の曲げに行く。