9章：梁の曲げ

    作成2011.11.22
    　梁の曲げにおける応力と撓みの公式は、機械設計便覧等に記載されており、多くの場合公式を用いて計算できます。
    　しかし、公式が適用できない特殊ケースもあります。このような場合、梁の曲げに関する基礎を理解する必要が生じます。

  1. 材料力学における座標軸の定義と正負の方向
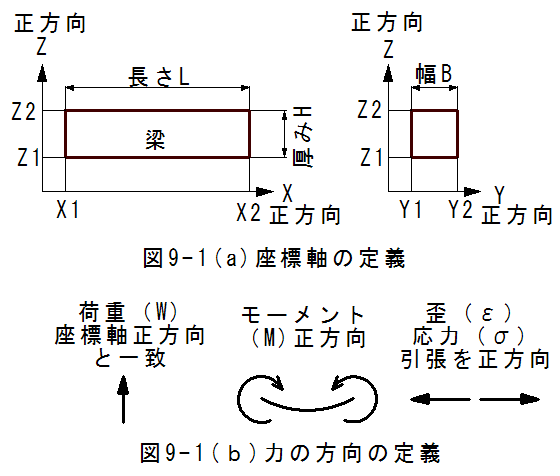
    　梁の曲げは3次元物体の変形を扱うため、座標軸の定義が必要となります。3次元座標は通常XYZ軸で表現されます。一般物理学では、高さ方向をZとし、高さが増す方向を正にするのが一般的です。しかし、機械工学では、重力方向をYとし、重力の向かう方向を正にする文献が多いのです。ここでは、 混乱をさけるため、一般物理学の座標軸の定義を採用したいと思います。

    　ここでは、梁の曲げの座標軸を一般物理学に合わせて、図9-1(a)に示すように定義します。また、 力の正方向を図9-1(ｂ)に示すように定義します。



  2. 集中荷重をうける片持梁における力のバランス
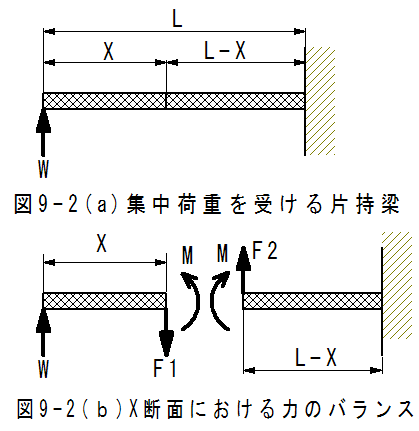
    　集中荷重をうける片持梁における力のバランスについて考えて見ましょう。
    　図9-2(a)に長さ（L)の集中荷重をうける片持梁を示します。
    　ここで図9-2(b)に示すように位置Xで分割した2個の要素を考えます。そして、分割した要素における力の バランスを考えるのです。
    　図9-2(b)の左側の要素において、荷重Wとせん断力F1はバランスする必要があります。すなわち

    　が成立必要があります。荷重Wとせん断力F1は方向が逆であり、WXのモーメントが発生します。




  3. 梁の曲げ応力
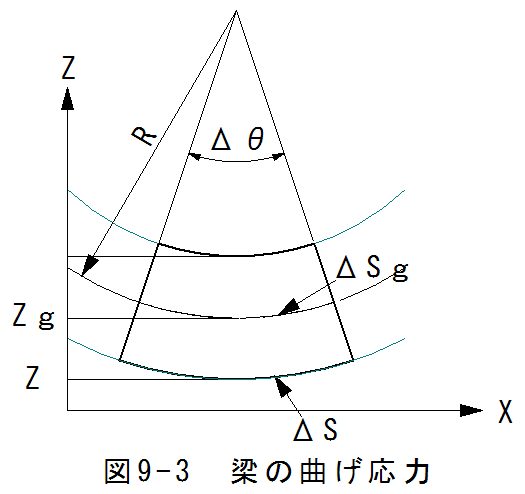
    　梁の曲げ応力の計算において、通常せん断応力の影響は無視します。
    　図9-3に梁の曲げ応力の説明図を示します。（図示していませんが、梁の幅方向をZ軸としています。）
    　図9-3においては、梁が曲率半径Rで曲げられた状態を示しています。梁が曲げられた場合、 長さが変化しない中立軸があります。この位置をZgとします。微小角度ΔθにおけるZgでの円弧の長さは

    　Z点での円弧の長さは

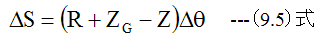
    　Z点での歪（ε）は

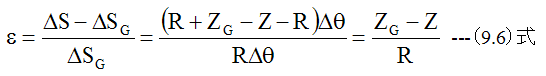
    　歪（ε）と応力（σ）は下記の関係式が成立します。

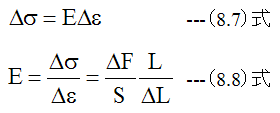
    　（9.6）式と（8.7）式から

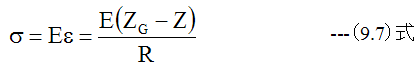
    　（9.7）式は応力（σ）が中立位置Zgからの距離に比例することを示しています。
    　また。 （9.7）式のEは縦弾性係数（ヤング率）です。



  4. 応力のバランス
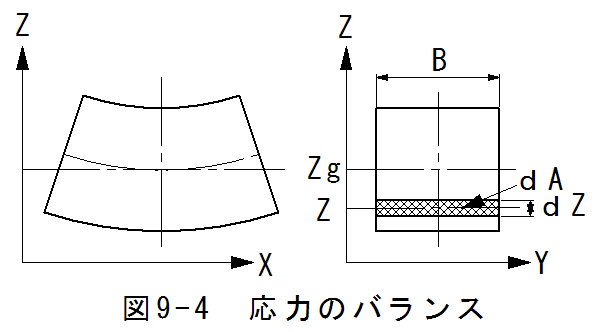
    　図9-4に応力のバランス説明図を示します。
    　図9-4において、梁の長さ方向がX、撓み方向がZ、幅方向がYとなっています。
    　力のバランスから、断面における応力の総和がゼロとなる必要があります。すなわち

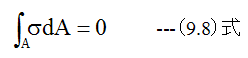
    　（9.8）式に（9.7）式を代入すると

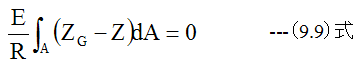
    　（9.9）式を変形すると

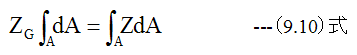
    　（9.10）式左辺はZgと断面積の積であり、右辺は断面1次モーメントです。梁の断面が幅Bの長方形で、Zが0からHまで変化するとするならば、 （9.10）式は下記のようになります。

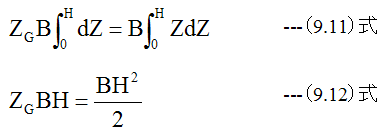
    　すなわち

    　断面が長方形の場合、（9.13）式の結果は、面倒な式の展開を行わなくても直感的に予想できます。しかし非対称な断面形状の場合は、 （9.10）式から中立軸の位置を求める必要があります。



  5. 応力によるモーメント
    　応力によるモーメントの総和（M）は

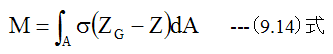
    　となります。 （9.14）式に（9.7）式を代入すると

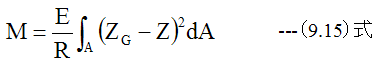
    　ここで断面2次モーメントを下記式で定義します。

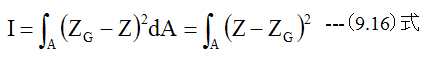
    　梁の断面が幅Bの長方形で、Yが0からHまで変化するとするならば、 （9.16）式は下記のようになります。

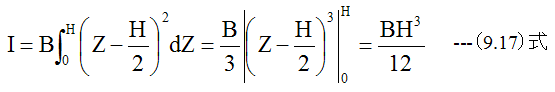
    　（9.17）式は長方形の断面2次モーメントの公式として有名です。
    　したがって、長方形断面のモーメントは

    　となります。
    　また、図9-1に示す片持梁のモーメントは

    　であり、 （9.18）式を代入すると

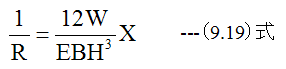
    　（9.19）式において変数は曲率半径Rと位置Xのみです。曲率半径Rの逆数が位置Xと比例することがわかります。


  6. 梁の曲げの基礎方程式
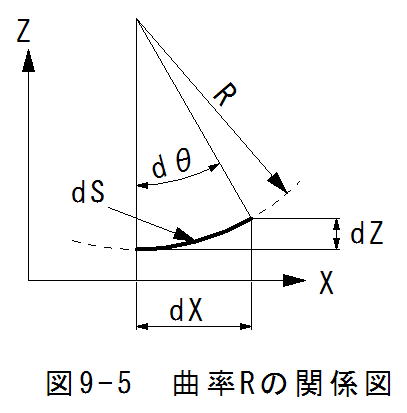
    　図9-5に曲率RとXZ座標系との関係図を示します。
    　図9-5において微小角度Δθでの円弧ΔSの長さは、

    　が成立します。微小角度Δθにおいて

    　（9.21）式を（9.20）式に代入して整理すると

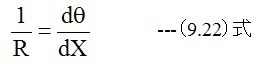
    　となります。円弧の角度θは

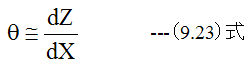
    　（9.23）式を（9.22）式に代入すると

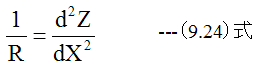
    　（9.19）式に（9.24）式を代入すると

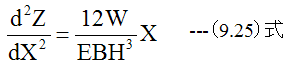
    　となります。 （9.25）式は長方形断面の梁の曲げの基礎方程式です。一般化するため


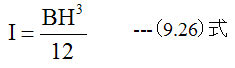
    　（9.25）式に（9.2）式と（9.26）式を代入すると

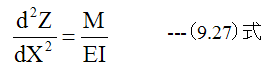
    　となります。 （9.27）式が梁の曲げ撓みの基礎方程式です。



  7. 曲げの応力の基礎方程式
    　材料の強度を確認するには応力を求める必要があります。


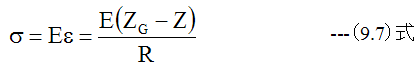
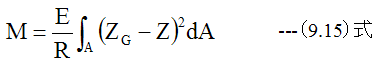
    　（9.15）式を断面2次モーメントIを用いて変形すると

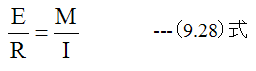
    　（9.7）式に（9.28）式を代入すると

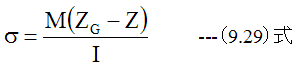
    　となります。 （9.29）式が曲げの応力の基礎方程式です。



  8. 長方形断面、片持梁の撓みと応力の計算式
    　片持梁の撓みと応力の計算式を求めます。
    　まずは、下記式の解を求めます。

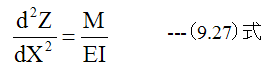
    　（9.27）式に（9.2）式を代入して

    　（9.30）式を積分して

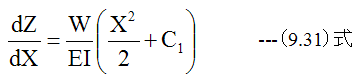
    　さらに積分して

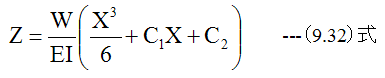
    　下記に条件で定数C1とC2を求めます。
    　X=Lにおいて

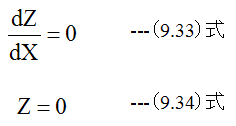
    　定数C1とC2は

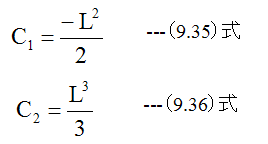
    　（9.32）式に（9.35）式と（9.36）式を代入して

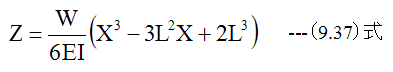
    　応力は

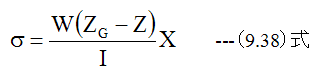
    　また


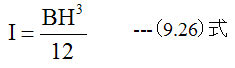
    　から具体的な値を計算できます。


  9. 長方形断面、片持梁の撓みと応力の計算例
    　代表的な機械材料SUS304の特性は
    縦弾性率　E=193000（N/mm2）
    耐力＝206（N/mm2）
    です。
    　計算条件として、
    ・縦弾性率　E=193000（N/mm2）
    ・梁の幅　B=10mm
    ・梁の厚さ　H=2mm
    ・梁の長さ　L=100mm
    ・荷重　　　　W=10N
    　で片持梁の撓みと応力の計算を行います。
    　片持梁の撓み計算結果グラフを以下に示します。


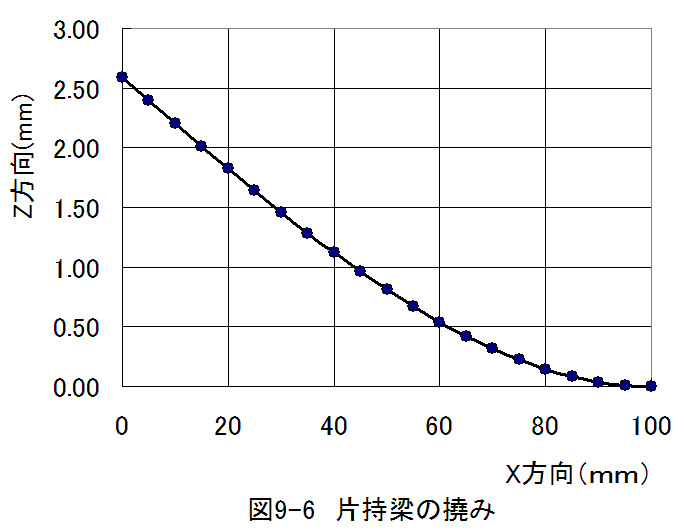
    　図9-6に示すように最大撓みはX=0mmの点であり、撓み量は 2.59mmとなります。

    　片持梁の応力の最大はX=100mmの点で発生します。
    　X=100mmの点におけるZ位置を変数とした応力の 計算結果をグラフを以下に示します。


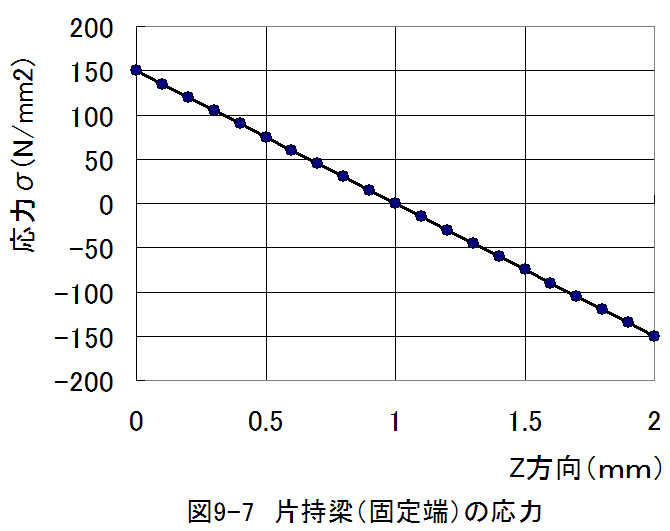
    　図9-7に示すように、応力の最大、最小はZ=0mmとZ＝2mmの 端で発生します。
    　基礎式の誘導の前提として、Zの正方向を上側、引張応力を正 としましたので、Z=0mmで引張、Z＝2mmで圧縮となります。
    　SUS304の耐力＝206（N/mm2）に対して、最大応力は 150（N/mm2）ですので、弾性変形の範囲内となります。


  10. 梁の曲げ纏め
    　梁の曲げにおける撓みと応力の計算式は公式が十分整備されていますので 通常の強度計算は公式の適用で済んでしまいます。
    　このため、基礎方程式の誘導の過程を忘れがちです。しかし、特殊ケースに おいては公式が適用できないケースもあります。このような場合、基礎式に戻る 必要があります。






１０章：断面2次モーメントの計算に行く。

トップページに戻る。