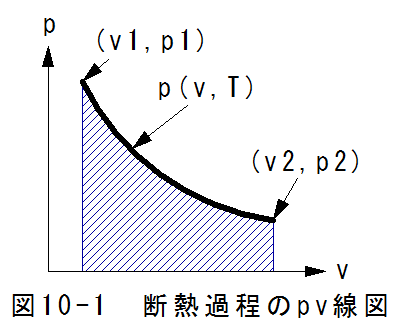
熱力学の第1法則
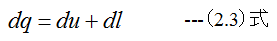
(2.3)式において、
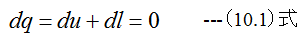
(10.1)式を満足する過程を断熱過程といいます。
(10.1)式を変形すると


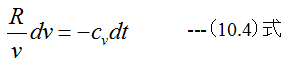
(10.4)式が断熱過程の基礎式となります。
初期の比容積をv1、最終比容積をv2、初期温度をt1、最終温度をt2としたとき
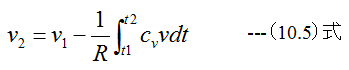

となります。(10.5)式の定容比熱cvは温度tで変化するため、 (10.5)式の積分は数値積分法を適用する必要があります。
空気が温度30℃の空気が、最初の圧力10000kp/m2から530℃まで断熱的に圧縮された。
温度変化10℃ごとの比容積、圧力、仕事エネルギーを求めよ。
ただし
絶対零度=-273℃
空気のガス定数R=29.27(mkp/kg・K)
温度変化10℃ごとの比容積の値は、表3-2 定容比熱cvの数表(単位:kcal/kg・deg)を補間して作成します。
解答
数値積分は、一番簡単な台形積分を使用します。
計算結果を表10-1に示します。
表10-1 断熱過程における温度変化10℃ごとの比容積、圧力、仕事エネルギー
| 温度 | 定容比熱cv | 定容比熱cv | 比容積v | 圧力p | 仕事l |
| ℃ | kcal/kg・deg | mkp/kg・deg | m3/kg | kp/m2 | mkp |
| 30 | 0.1720 | 73.44 | 0.8869 | 10000 | 0 |
| 40 | 0.1721 | 73.47 | 0.8348 | 10975 | -735 |
| 50 | 0.1721 | 73.50 | 0.7857 | 12033 | -1469 |
| 60 | 0.1722 | 73.53 | 0.7395 | 13181 | -2205 |
| 70 | 0.1723 | 73.56 | 0.6960 | 14426 | -2940 |
| 80 | 0.1723 | 73.59 | 0.6550 | 15775 | -3676 |
| 90 | 0.1724 | 73.62 | 0.6164 | 17237 | -4412 |
| 100 | 0.1725 | 73.65 | 0.5801 | 18820 | -5148 |
| 110 | 0.1729 | 73.81 | 0.5459 | 20537 | -5885 |
| 120 | 0.1733 | 73.98 | 0.5136 | 22397 | -6624 |
| 130 | 0.1737 | 74.15 | 0.4832 | 24414 | -7365 |
| 140 | 0.1740 | 74.32 | 0.4545 | 26599 | -8107 |
| 150 | 0.1744 | 74.49 | 0.4274 | 28968 | -8851 |
| 160 | 0.1748 | 74.65 | 0.4019 | 31534 | -9597 |
| 170 | 0.1752 | 74.82 | 0.3779 | 34314 | -10344 |
| 180 | 0.1756 | 74.99 | 0.3552 | 37326 | -11094 |
| 190 | 0.1760 | 75.16 | 0.3339 | 40588 | -11844 |
| 200 | 0.1764 | 75.33 | 0.3138 | 44121 | -12597 |
| 210 | 0.1769 | 75.53 | 0.2949 | 47948 | -13351 |
| 220 | 0.1774 | 75.74 | 0.2770 | 52093 | -14107 |
| 230 | 0.1779 | 75.95 | 0.2602 | 56583 | -14866 |
| 240 | 0.1783 | 76.15 | 0.2444 | 61447 | -15626 |
| 250 | 0.1788 | 76.36 | 0.2295 | 66715 | -16389 |
| 260 | 0.1793 | 76.57 | 0.2154 | 72422 | -17154 |
| 270 | 0.1798 | 76.77 | 0.2022 | 78602 | -17920 |
| 280 | 0.1803 | 76.98 | 0.1898 | 85296 | -18689 |
| 290 | 0.1808 | 77.19 | 0.1781 | 92546 | -19460 |
| 300 | 0.1812 | 77.39 | 0.1671 | 100399 | -20233 |
| 310 | 0.1818 | 77.64 | 0.1567 | 108905 | -21008 |
| 320 | 0.1824 | 77.88 | 0.1469 | 118122 | -21785 |
| 330 | 0.1830 | 78.13 | 0.1378 | 128110 | -22565 |
| 340 | 0.1836 | 78.38 | 0.1291 | 138934 | -23348 |
| 350 | 0.1841 | 78.62 | 0.1210 | 150663 | -24133 |
| 360 | 0.1847 | 78.87 | 0.1134 | 163375 | -24920 |
| 370 | 0.1853 | 79.12 | 0.1062 | 177152 | -25710 |
| 380 | 0.1859 | 79.36 | 0.0995 | 192085 | -26503 |
| 390 | 0.1864 | 79.61 | 0.0932 | 208272 | -27298 |
| 400 | 0.1870 | 79.85 | 0.0872 | 225819 | -28095 |
| 410 | 0.1876 | 80.09 | 0.0817 | 244842 | -28895 |
| 420 | 0.1881 | 80.33 | 0.0764 | 265464 | -29697 |
| 430 | 0.1887 | 80.57 | 0.0715 | 287822 | -30501 |
| 440 | 0.1893 | 80.82 | 0.0669 | 312065 | -31308 |
| 450 | 0.1898 | 81.06 | 0.0625 | 338353 | -32118 |
| 460 | 0.1904 | 81.30 | 0.0585 | 366860 | -32929 |
| 470 | 0.1910 | 81.54 | 0.0547 | 397777 | -33744 |
| 480 | 0.1915 | 81.78 | 0.0511 | 431309 | -34560 |
| 490 | 0.1921 | 82.02 | 0.0478 | 467683 | -35379 |
| 500 | 0.1926 | 82.26 | 0.0446 | 507141 | -36200 |
| 510 | 0.1932 | 82.49 | 0.0417 | 549948 | -37024 |
| 520 | 0.1937 | 82.73 | 0.0389 | 596392 | -37850 |
| 530 | 0.1943 | 82.96 | 0.0363 | 646786 | -38679 |
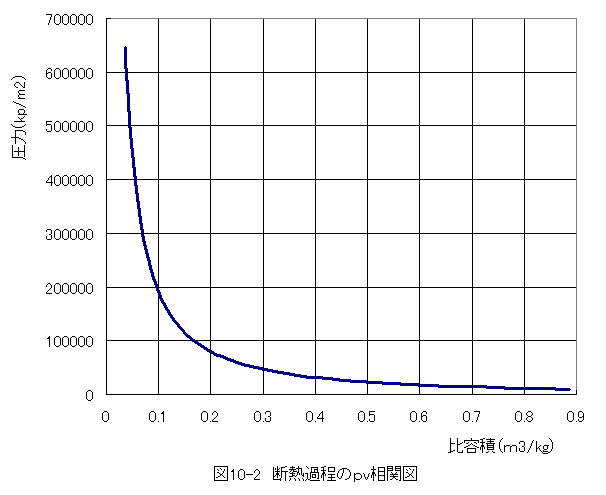
表10-1 断熱過程における温度変化10℃ごとの比容積、圧力、仕事エネルギーにおいて、仕事がマイナスになっ ていますがこれは、外部から圧縮の仕事が必要なこと示しています。
図10-2に断熱過程のpv相関図を示します。
熱力学の基礎式の多くは微分形で表現されます。具体的な変数の値を知るには積分演算が必 要となります。特定の条件においては代数的に解くことができますが、比熱ように値が数表で 与えられる場合は代数的にとくことが困難です。このような場合は数値積分が有効です。現在はパソコ ンの性能が大幅に向上しており、数値積分は簡単に実行できます。
比熱が一定値の場合は代数解を求めることができます。

(10.6)式は
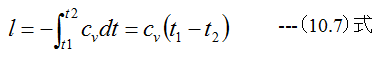
となります。比熱の関係式は
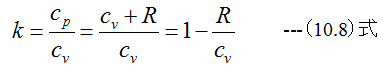
から
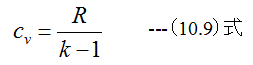
また
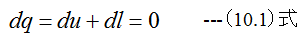
から
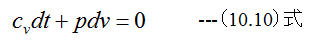
(10.10)式に(10.9)式を代入すると
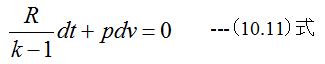
すなわち
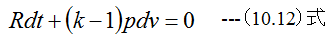
一方
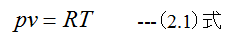
を微分すると
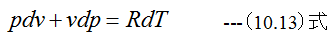
(10.12)式に(10.13)式を代入して
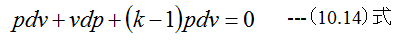
(10.14)式を整理すると

(10.15)式をpvで割ると

微分方程式(10.16)式の解は
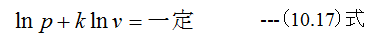
(10.17)式は以下のように変形できます。
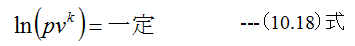

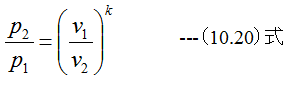
となります。
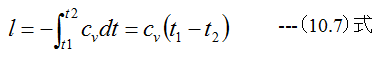
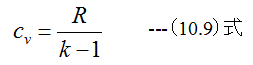
(10.7)式に(10.9)式を代入すると
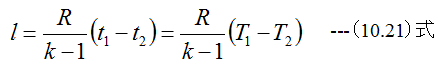
になり
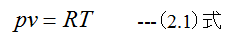
から
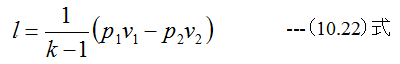
(10.22)式を書き換えると
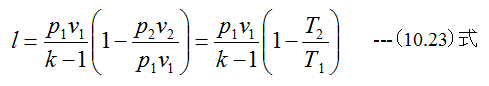
(10.23)式に(10.20)式を代入すると
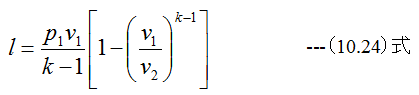
最後に
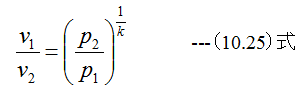
(10.24)式に(10.25)式を代入すると
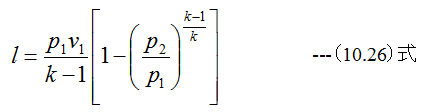
(10.23)式、 (10.24)式、 (10.26)式を比較すると
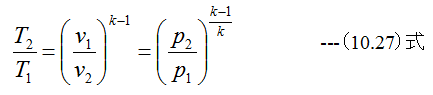
の関係が得られます。 (10.27)式から

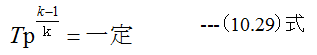
の関係も得られます。
空気が温度30℃の空気が、最初の圧力10000kp/m2から530℃まで断熱的に圧縮された。
温度変化10℃ごとの比容積、圧力、仕事エネルギーを求めよ。
ただし
絶対零度=-273℃
空気のガス定数R=29.27(mkp/kg・K)
(10.27)式を使用して計算、k=cp/cv=1.4、cv=0.172(kcal/kg・deg)=73.440 (mkp/kg・deg)とします。
解答
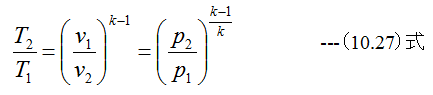
(10.27)式を変形して

計算結果を表10-2に示します。
表10-2 断熱過程(代数解)における温度変化10℃ごとの比容積、圧力、仕事エネルギー
| 温度 | 比容積v(k=一定) | 圧力p(k=一定) | 仕事l(cv=一定) | 比容積v(数値積分) | 圧力p(数値積分) |
| ℃ | m3/kg | kp/m2 | mkp | m3/kg | kp/m2 |
| 30 | 0.8869 | 10000 | 0 | 0.8869 | 10000 |
| 40 | 0.8177 | 11204 | 734 | 0.8348 | 10975 |
| 50 | 0.7559 | 12507 | 0 | 0.7857 | 12033 |
| 60 | 0.7004 | 13916 | -734 | 0.7395 | 13181 |
| 70 | 0.6505 | 15434 | -1469 | 0.6960 | 14426 |
| 80 | 0.6054 | 17067 | -2203 | 0.6550 | 15775 |
| 90 | 0.5646 | 18820 | -2938 | 0.6164 | 17237 |
| 100 | 0.5275 | 20698 | -3672 | 0.5801 | 18820 |
| 110 | 0.4937 | 22706 | -4406 | 0.5459 | 20537 |
| 120 | 0.4629 | 24850 | -5141 | 0.5136 | 22397 |
| 130 | 0.4347 | 27134 | -5875 | 0.4832 | 24414 |
| 140 | 0.4089 | 29565 | -6610 | 0.4545 | 26599 |
| 150 | 0.3851 | 32147 | -7344 | 0.4274 | 28968 |
| 160 | 0.3633 | 34887 | -8078 | 0.4019 | 31534 |
| 170 | 0.3431 | 37789 | -8813 | 0.3779 | 34314 |
| 180 | 0.3245 | 40860 | -9547 | 0.3552 | 37326 |
| 190 | 0.3073 | 44105 | -10282 | 0.3339 | 40588 |
| 200 | 0.2913 | 47530 | -11016 | 0.3138 | 44121 |
| 210 | 0.2764 | 51141 | -11750 | 0.2949 | 47948 |
| 220 | 0.2626 | 54943 | -12485 | 0.2770 | 52093 |
| 230 | 0.2498 | 58944 | -13219 | 0.2602 | 56583 |
| 240 | 0.2378 | 63148 | -13954 | 0.2444 | 61447 |
| 250 | 0.2266 | 67563 | -14688 | 0.2295 | 66715 |
| 260 | 0.2161 | 72193 | -15422 | 0.2154 | 72422 |
| 270 | 0.2063 | 77046 | -16157 | 0.2022 | 78602 |
| 280 | 0.1971 | 82128 | -16891 | 0.1898 | 85296 |
| 290 | 0.1885 | 87444 | -17626 | 0.1781 | 92546 |
| 300 | 0.1803 | 93002 | -18360 | 0.1671 | 100399 |
| 310 | 0.1727 | 98808 | -19094 | 0.1567 | 108905 |
| 320 | 0.1655 | 104868 | -19829 | 0.1469 | 118122 |
| 330 | 0.1587 | 111189 | -20563 | 0.1378 | 128110 |
| 340 | 0.1523 | 117778 | -21298 | 0.1291 | 138934 |
| 350 | 0.1463 | 124640 | -22032 | 0.1210 | 150663 |
| 360 | 0.1406 | 131784 | -22766 | 0.1134 | 163375 |
| 370 | 0.1352 | 139216 | -23501 | 0.1062 | 177152 |
| 380 | 0.1301 | 146942 | -24235 | 0.0995 | 192085 |
| 390 | 0.1252 | 154970 | -24970 | 0.0932 | 208272 |
| 400 | 0.1206 | 163307 | -25704 | 0.0872 | 225819 |
| 410 | 0.1163 | 171958 | -26438 | 0.0817 | 244842 |
| 420 | 0.1121 | 180933 | -27173 | 0.0764 | 265464 |
| 430 | 0.1082 | 190237 | -27907 | 0.0715 | 287822 |
| 440 | 0.1044 | 199878 | -28642 | 0.0669 | 312065 |
| 450 | 0.1008 | 209862 | -29376 | 0.0625 | 338353 |
| 460 | 0.0974 | 220199 | -30110 | 0.0585 | 366860 |
| 470 | 0.0942 | 230893 | -30845 | 0.0547 | 397777 |
| 480 | 0.0911 | 241954 | -31579 | 0.0511 | 431309 |
| 490 | 0.0881 | 253388 | -32314 | 0.0478 | 467683 |
| 500 | 0.0853 | 265203 | -33048 | 0.0446 | 507141 |
| 510 | 0.0826 | 277407 | -33782 | 0.0417 | 549948 |
| 520 | 0.0800 | 290006 | -34517 | 0.0389 | 596392 |
| 530 | 0.0776 | 303009 | -35251 | 0.0363 | 646786 |
図10-3に断熱過程のpv相関比較図を示します。
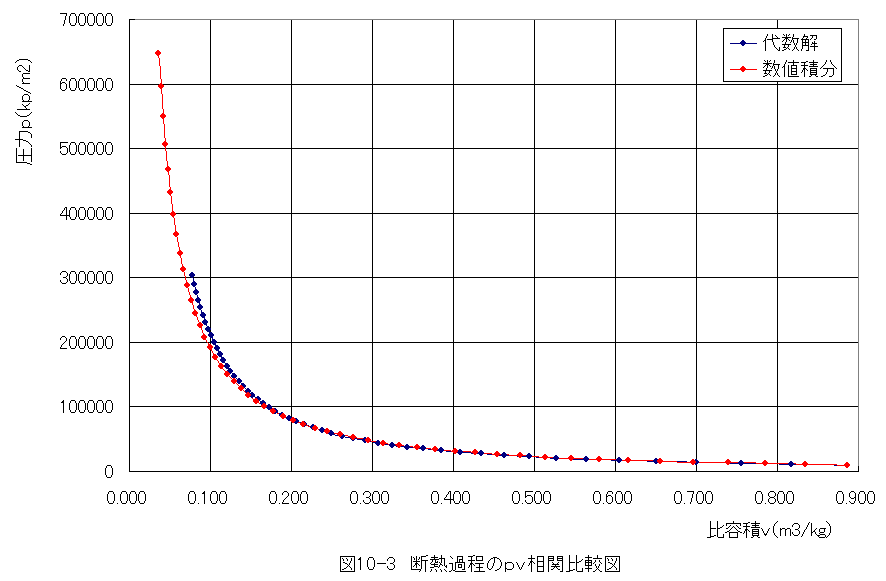
代数解はk=cp/cv=一定と仮定しています。k=一定と仮定しないと代数解の誘導が難しいためです。これに対して数値積分法においては、比 熱cvが数表で与えられれば計算可能です。
図10-3から代数解は数値積分法に対して誤差を生じることが確認できます。断熱過程における 代数解はあくまでも近似計算として判断する必要があります。