横軸にエントロピs、縦軸に温度TをとったグラフをTs線図、または熱線図といいます。
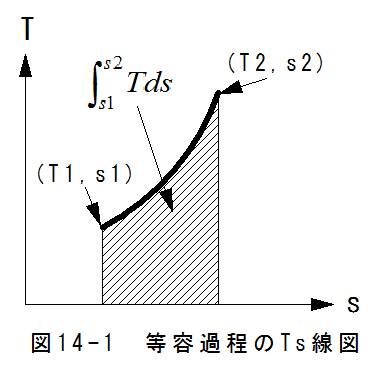
等容過程等容過程ではv=一定となります。従って、エントロピの関係式
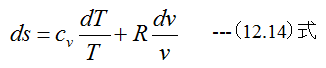
（12.14）式は
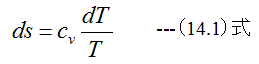
となります。 （14.1）式を初期値s1、T1、終値をs2、T2として積分すると
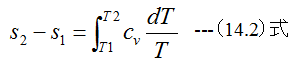
Cv＝一定とすると
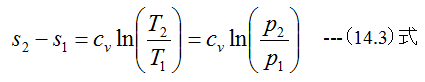
となります。 （14.3）式を変形すると
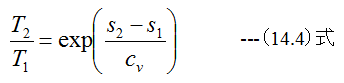
となり、温度Tはsの増加に伴い指数関数的に増大する曲線となります。
エントロピの定義式
（12.8）式から
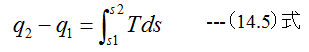
となります。また等容過程ではq=uであり
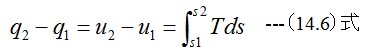
となります。 （14.6）式に（14.1）式を代入すると
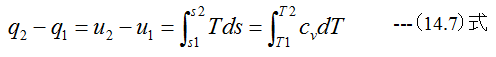
ここでcv＝一定とするならば
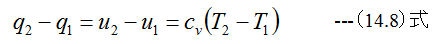
となります。
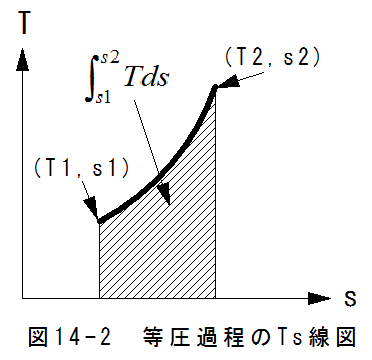
等圧過程等圧過程ではp=一定となります。従って、エントロピの関係式
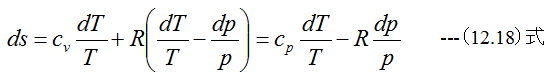
（12.18）式は
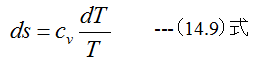
となります。 （14.9）式を初期値s1、T1、終値をs2、T2として積分すると
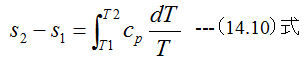
Cp＝一定とすると
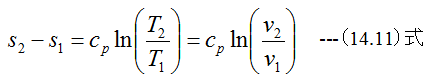
となります。 （14.11）式を変形すると
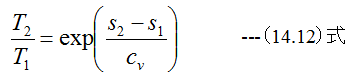
となり、温度Tはsの増加に伴い指数関数的に増大する曲線となります。
エントロピの定義式
（12.8）式から
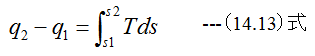
となります。 （14.13）式に（14.9）式を代入すると
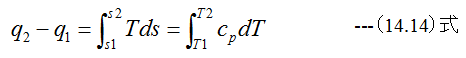
ここでcp＝一定とするならば
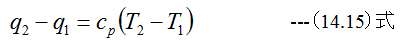
となります。
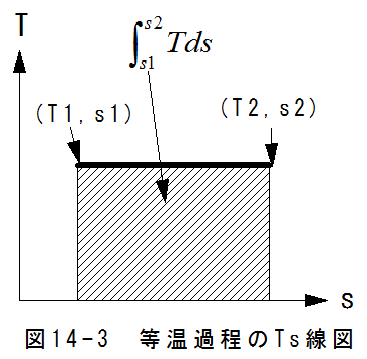
等温過程等温過程ではT=一定となります。従って、エントロピの関係式
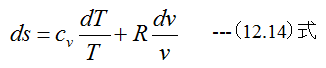
（12.14）式は
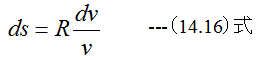
となります。 （14.16）式を初期値s1、ｖ1、終値をs2、ｖ2として積分すると
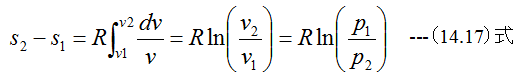
エントロピの定義式
（12.8）式から
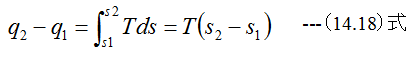
となります。 また等温過程においてはｑ＝ｌの関係があり
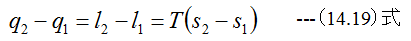
となります。
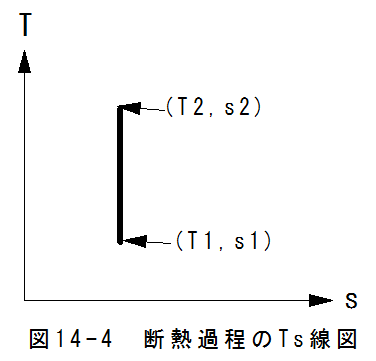
断熱過程断熱過程ではdq=0となります。従って、エントロピの関係式
（12.8）式は
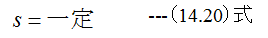
となります。また比熱が一定の場合は下記の式が成立します。
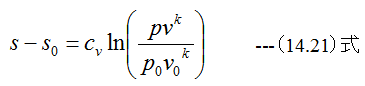
（14.21）式においてs=一定とするならば
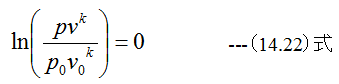
すなわち
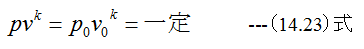
となります。
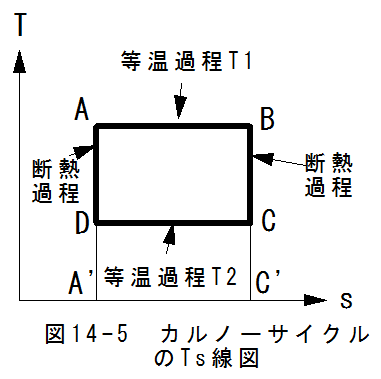（１） Ts熱線図におけるカルノーサイクルTs熱線図におけるカルノーサイクルを図14-5に示します。
図14-5において過程ABで供給される熱量q1は
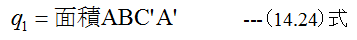
となります、過程CDで放出される熱量q2は
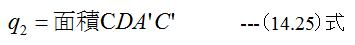
したがって、このカルノーサイクルの効率ηは
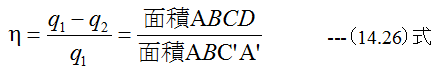
となります。
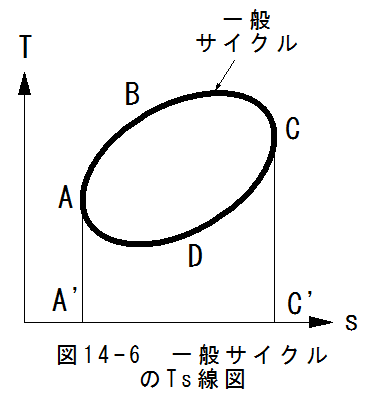
（２） Ts熱線図における一般サイクルTs熱線図における一般サイクルを図14-6に示します。
図14-6において過程ABCで供給される熱量q1は
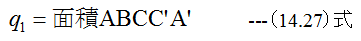
となります、過程CDAで放出される熱量q2は
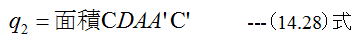
したがって、このカルノーサイクルの効率ηは
となります。
Ts熱線図を用いるとサイクルの効率計算が容易に行えることがわかります。また、熱機関の効率は高温側と低 温側の差が大きいほど効率が向上することが容易に理解できます。
１５章：オットーサイクル(otto cycle)に行く。