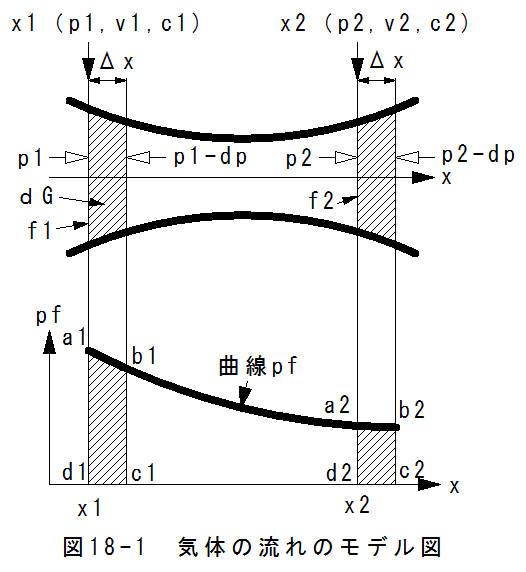
連続の条件図18-1に気体の流れのモデル図を示します。
図18-1において、気体はx軸の正方向に移動しているとします。管の軸は直線であるが、その断面積ｆは一定でなく、気体の 速度ｃも一定でないと考えます。
気体は管を満たし、その状態を変えながら運動します。各断面の状態は圧力pと比容積ｖで定まり、各断面のp,v,cは一定 の値をとります。例えば断面ｘ1ではp1,v1,c1をとり、断面ｘ2ではp2,v2.c2となります。
一定時間に管の断面を通過する気体の質量Gどの断面に対しても同じで、時間がたっても変わりません。従って
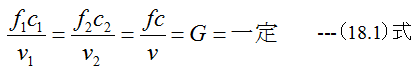
Gは1秒間の気体の消費量（kg/s)です。おのおのの断面を一定時間に通過して流れる気体の質量が一定であることは運動 の連続性を示し、このことから（17.1）式は連続の条件と呼びます。
気体の運動エネルギー図18-1において位置ｘ1と位置ｘ2の間にある気体1kg対しての仕事をl’とします。微小な気体dGに対しての仕事は l’dGとなります。
流れの方向に作用する外圧の仕事は
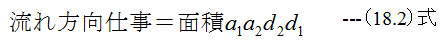
流れと逆方向に作用する外圧の仕事は
従って
Δｘが十分小さいとするならば
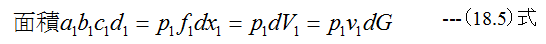
（18.4）式に（18.5）式、 （18.6）式を代入すると
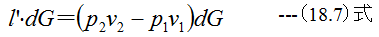
従って
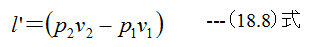
を得る。無限小状態変化に対して
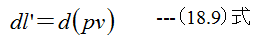
となります。
熱力学第1法則の方程式をエネルギ保存の法則として速度ｃが変化する流れに適用する場合には、右辺に巨視的な運動エネル ギの変化を付け加えなければいけません。
熱力学第1法則の方程式
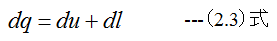
（2.3）式式は以下のように変化します。
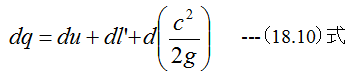
（18.10）式のgは変換定数でありg=9.8(N/kp)です。これは、工学単位を物理単位に変換する定数です。 （18.10）式に （18.9）式を代入すると
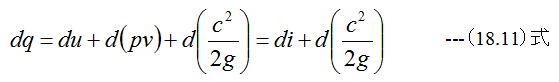
（18.11）式のiはエンタルピであり以下の関係式が成立します。
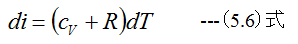
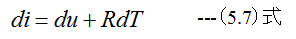
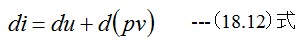
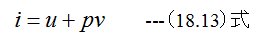
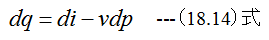
（18.11）式は気体の流れの基礎となるもので、噴射の際の可逆過程に対しても、不可逆過程に対しても成り立つ、この ことは次のように表現されます。
「一般的に、流れの間に物体が受取る熱量は2つのことに消費される。その一部はエンタルピの増加に、残りは外部運動エ ネルギ、すなわち流れの速度増加に費やされる。」
流れ過程の有効仕事下記の式を組合わせると
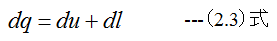
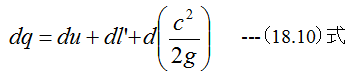
2つの仕事量の差dｌ0＝dl-dl’は
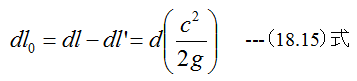
となります。気体の運動エネルギの増加は一種の有効仕事であり、目的によってはこれを利用できます。たとえばタービ ンでは、気体は膨張の結果かなりの速度で噴射され、回転子の羽を通り抜けてその速度を失い、その際失った外部運動エネル ギがタービンの軸を回転させて仕事をする。
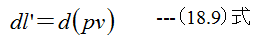
（18.15）式に（6.2）式と（18.9）式を代入すると
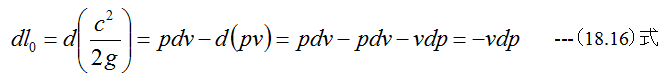
同様に
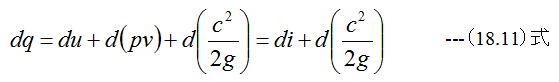
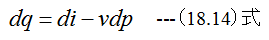
（18.11）式と（18.14）式を組合わせると
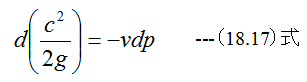
となり、（18.16）式と一致します。 （18.17）式は次のように変形できます。
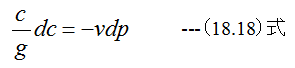
（18.18）式式からdcとdp反対の符号を持っていることがわかる。言い換えると「可逆過程では、速度の増加は圧力の減少と 密接な関係を持ち、あるいはその逆に速度の減少は圧力の増加を伴うということである。」
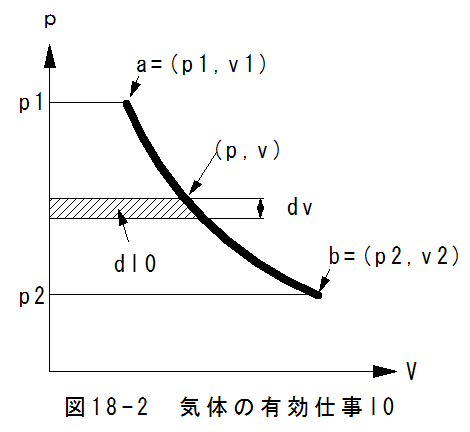
流れ過程の有効仕事気体の有効仕事の関係図を図18-2に示します。図18-2において、圧力が曲線abに従って変化するとします。
図18-2の斜線の部分の面積は
であり、a点からb点までの有効仕事ｌ0は
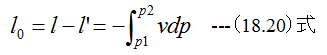
となります。曲線abをポリトロープ曲線とすると
（17.1）式から
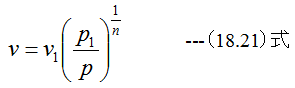
（18.20）式に（18.21）式を代入して積分を実行すると
となります。またポリトロープの仕事の式は
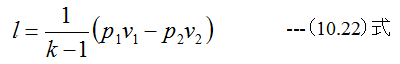
（10.22）式のkをnに置き換えた式となります。従って
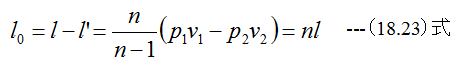
有効仕事はポリトロープの指数によって膨張の仕事より大きくもなれば小さくもなる。例えば等温変化では、n＝1であ るから、ｌ0＝ｌになりｌ’=0である。Ｔ＝一定ならばｐｖ＝一定であり、dl’=d(pv)=0となる。
空気が断熱膨張するときには、n=1.4であるから、有効仕事は膨張の仕事より40%おおきくなり、l’<0で外部からの仕事 が消費される。
変化は等容線の場合、膨張の仕事はｌ＝0となるが
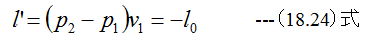
となります。
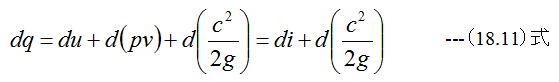
（18.11）式から
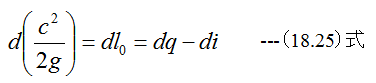
が得られます。このことは、「一般に有効仕事は外の熱源から入った熱量と一定圧力におけるエンタルピで与えられる。」
有限な過程では、
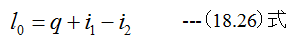
となります。エンタルピの関係式としては、
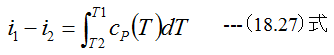
となります。
１９章：気体の断熱的な流れ過程に行く。