熱落差
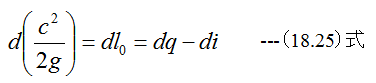
断熱過程においては、dq=0であり（18.25）式は
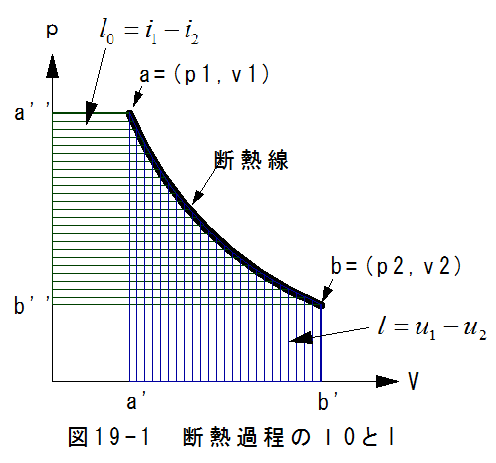
となります。図19-1に示す有限な断熱過程において、有効仕事ｌ0は面積abb’’a’’に等しく
となります。膨張の仕事ｌは面積abb’a’に等しく
となります。従って有効仕事は膨張仕事のk倍となります。
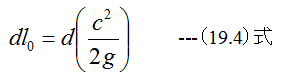
（19.4）式を積分すると
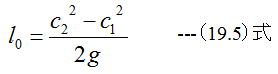
（19.5）式においてｃ1は気体の最初の速度、ｃ2は最後の速度です。c1=0、c2=cとするならば
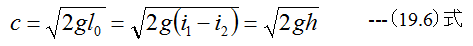
（19.6）式において、h=i1-i2であり、熱落差といいます。単位は通常kcal/kgを用いますが、工学統一単位mkp/kgに 変換するには1/A=427（mkp/kcal）をかける必要があります。
g=9.81N/kp、1/A= 427（mkp/kcal）として計算した結果のグラフを図19-2に示します。
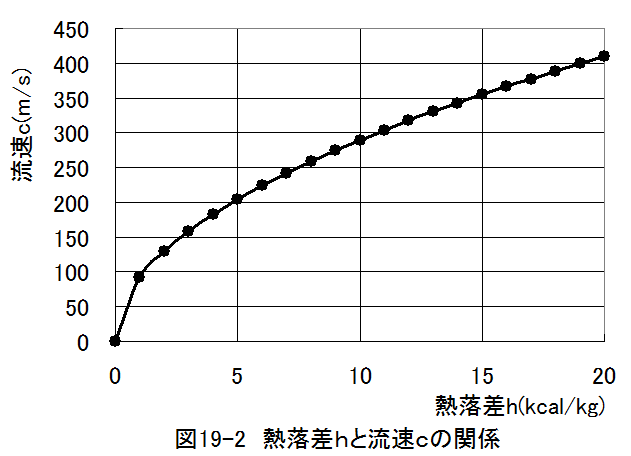
図19-2から熱落差を大きくすると音速を超えることがわかります。
圧力差による流速
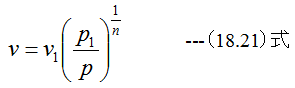
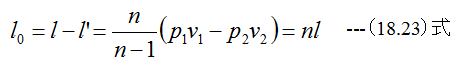
（18.21）式と（18.23）式において、n=kとして整理すると
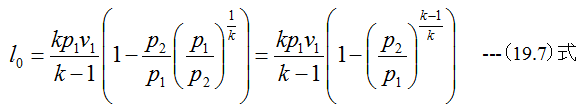
となります。気体の流速は（19.6）式から
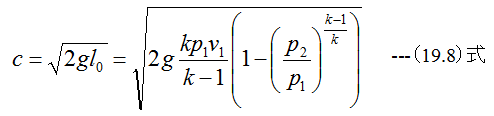
となります。
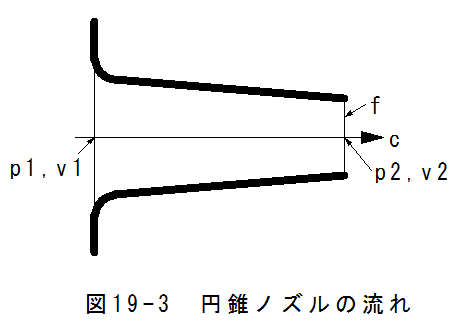
円錐ノズルで消費される気体の質量G図19-3に円錐ノズルの流れのモデル図を示します。
最初の状態をp1,v1で流速c=0とします。
ノズルの先端の断面積をfとします。先端の状態をp2,v2で流速をcとします。
消費される気体の重量は
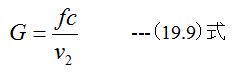
また
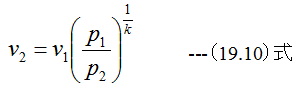
（19.9）式に（19.8）式と（19.10）式を代入して整理すると
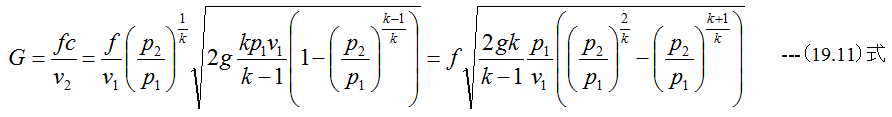
となります。
円錐ノズルで消費される気体の質量G計算例図19-3の円錐ノズルにおいて先端の直径がφ10mmとし、初期圧力p1=40000kp/m2、温度20℃とした場合、 ノズル先端の「圧力p2と流速cの関係」と「圧力p2と消費される気体の質量Gの関係 」を計算してグラフにせよ。
「圧力p2と流速cの関係」計算結果グラフを図19-4に示します。
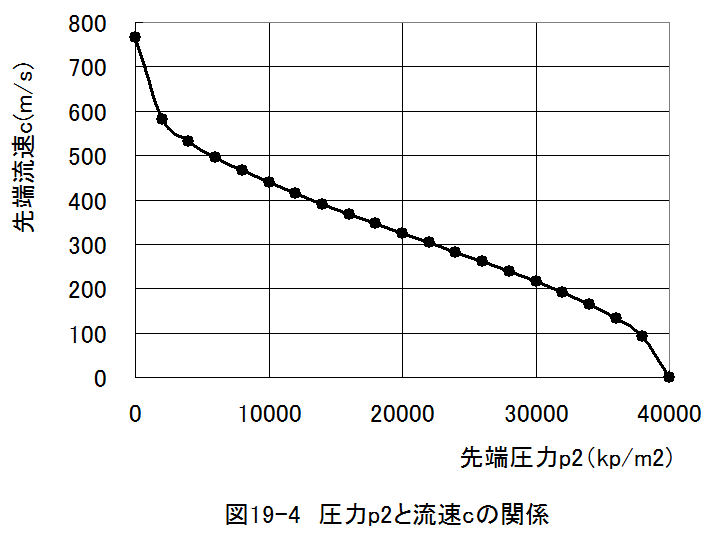
「圧力p2と消費される気体の質量Gの関係 」計算結果グラフを図19-5に示します。
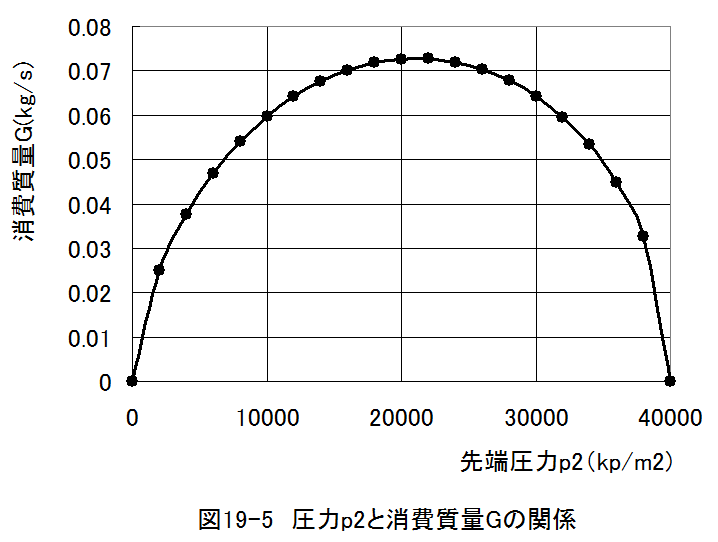
図19-5の「圧力p2と消費される気体の質量Gの関係 」のグラフから、先端部圧力p2が40000kp/m2から低下するに従って 最初は消費質量が増大しますが、特定の圧力で最大となり、その後は圧力の低下に従って低下しています。
実際には、圧力の低下に伴って消費質量Gは低下しないで一定となります。また、消費質量が最大となる先端部圧 力p2における流速はほぼ音速に達していることが図19-4でわかります。
図19-5の結果は次のように解釈します。
（１）圧力差が十分な場合、円錐状ノズルの先端部で流速が音速に達する。
（２）円錐状ノズルの先端部の圧力は外部圧力より高くなる。
（３）円錐状ノズルから流出後にさらに膨張し流速を増す。
（４）気体の流れは連続の条件を満足するように仮想的な流れを形成する。
（５）円錐状ノズルの先端部を通過後は膨張により末広がりの流れを形成する。
従って、臨界圧力pcrが存在し、消費量Gが一定になると思われます。
臨界圧力pcrと臨界流速ccr臨界圧力pcrは（19.11）式の微分がゼロとなる圧力を求めます。
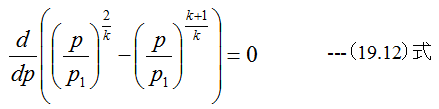
（19.12）式を微分すると
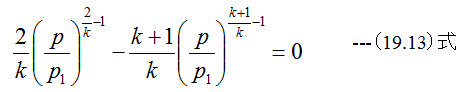
（19.13）式を変形すると
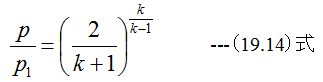
となります。従って
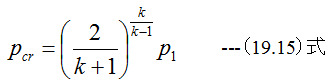
が得られます。Ｋ＝1.4とした場合、
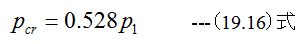
となります。臨界流速ccrは（18.8）式に（18.15）式を代入して
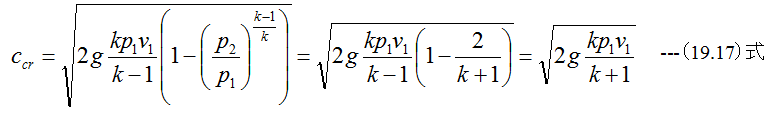
となります。
初期圧力p1=40000kp/m2、温度20℃とした場合、v1=0.214 m3/kgとなります。Ｋ＝1.4とした場合
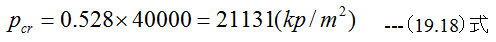
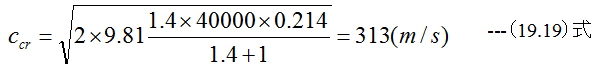
となります。
臨界流速ccrは音速に近い値となりますが、正確には異なります。
２０章：運動の連続条件と音速に行く。