１８章気体の断熱的な流れ過程では、図18-3に円錐ノズルの流れのモデル図での流れを検討しました。円錐ノズルは先端部で形状が不連続に変化する ため、 運動の連続条件を満足しているのか？疑問が生じます。
図18-3に円錐ノズルから導かれる臨界速度は１９章の音速の式と厳密には一致しません。
運動の連続条件を満足する断熱過程の流れのノズル形状について検討する必要があります。
計算式（１）運動の連続条件と音速から
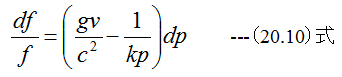
（２）１８章：空気圧縮機とポリトロープ過程から
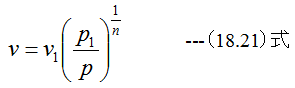
（３） １９章：気体の断熱的な流れ過程から
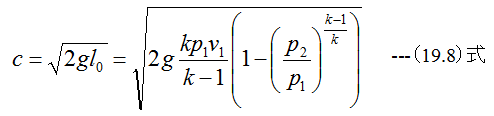
(20.10)式の変数の数はf、v、c、pの4個です。vは（18.21）式、cは（19.8）式で与えられます。従って(20.10)式はpとf の関係として解くことができます。
（20.10）式は微分方程式であり、これに（18.21）式、cは（19.8）式を代入して代数解を求めるのは難しそうで す。 (20.10)式、 （18.21）式、 （19.8）式は変形することなく連立式のまま数値計算で解を求めたいと思います。
計算結果計算条件は
円錐ノズルで消費される気体の質量G計算例
図19-3の円錐ノズルにおいて先端の直径がφ10mmとし、初期圧力p1=40000kp/m2、温度20℃と同じにします。
計算結果を図21-1のグラフにしめします。
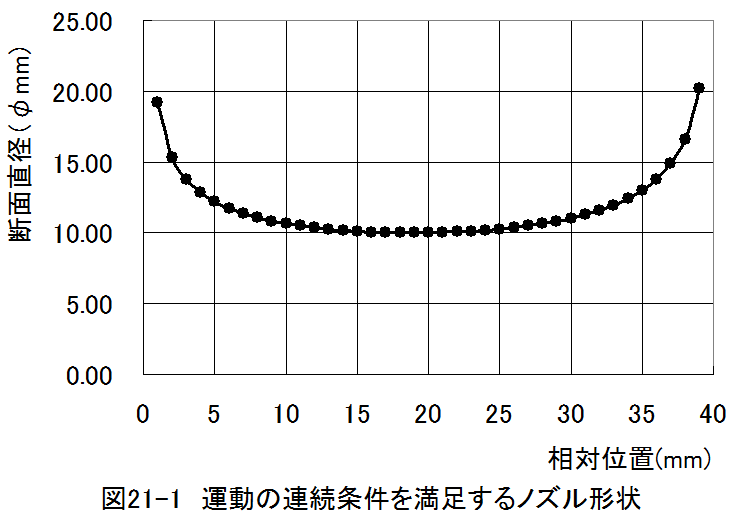
図21-1において、横軸は相対位置としましたが、圧力が1000kp/m2毎の減圧位置と対応しています。
圧力が40000kp/m2の点と0kp/m2の点は特異点で計算不能です。
なお、最小断面における流速は臨界流速となり、音速とはずれが生じます。（グラフは図18-4に一致します。）
２２章：タービンとジェットエンジンのサイクルに行く。