３５章：湿り蒸気の断熱的な流れ過程

    作成2012.07.30

  1. 湿り蒸気の断熱的な変化の計算
    　図19-3の円錐ノズルにおいて先端の直径がφ10mmとし、初期圧力p1=40000kp/m2、初期温度300℃とした場合
    　 （19.6）式と（19.9）式を使って、過熱蒸気の断熱的な流れ過程の計算を行うには、エントロピ一定での各圧力におけ るエンタルピと比容積の値を計算する必要があります。
    　この計算はワークブック「加熱蒸気表.xls」と「ゴールシーク」の機能を使って計算できますが、多くの単純作業の繰り 返し操作が必要となります。（たぶん面倒な作業でうんざりするでしょう！！）

    　 　このような場合、EXCELのVBAプログラムを利用すると効率的に計算できます。


  2. 湿り蒸気の断熱過程計算のワークブック「湿り蒸気断熱.xls 」のダウンロード
    　下記のワークブック「湿り蒸気断熱.xls」をダウンロードしてください。

    　ダウンロード後はダブルクリックで解凍してから使用してください。
    　     ワークブック「湿り蒸気断熱.xls 」をダウンロードする。


  3. ワークブック「湿り蒸気断熱.xls 」説明
    1. シート「操作」は計算条件の設定と計算結果の表示を行います。
    2. シート「湿り蒸気表」は湿り蒸気数表です。


  4. 湿り蒸気の断熱変化計算結果
    　ワークブック「湿り蒸気断熱.xls 」から下記の表を作成します。

    表35-1　湿り蒸気の断熱変化計算結果
    温度 圧力 エントロピ 比容積 エンタルピ 乾き度ｘ
    ℃ ata(kp/cm2） kcal/kg・deg m3/kg kcal/kg 無次元
    142.9 4.0 1.6478 0.4727 653.2 1.0000
    141.9 3.9 1.6478 0.4833 652.1 0.9984
    141.0 3.8 1.6478 0.4938 651.0 0.9969
    140.1 3.7 1.6478 0.5043 649.8 0.9953
    139.1 3.6 1.6478 0.5176 648.6 0.9935
    138.1 3.5 1.6478 0.5314 647.4 0.9916
    137.1 3.4 1.6478 0.5451 646.1 0.9897
    136.1 3.3 1.6478 0.5588 644.8 0.9878
    135.1 3.2 1.6478 0.5724 643.6 0.9859
    133.9 3.1 1.6478 0.5902 642.2 0.9839
    132.8 3.0 1.6478 0.6083 640.7 0.9818
    131.7 2.9 1.6478 0.6263 639.3 0.9797
    130.5 2.8 1.6478 0.6443 637.9 0.9776
    129.3 2.7 1.6478 0.6656 636.3 0.9754
    128.0 2.6 1.6478 0.6896 634.7 0.9731
    126.7 2.5 1.6478 0.7135 633.0 0.9708
    125.4 2.4 1.6478 0.7373 631.4 0.9685
    124.0 2.3 1.6478 0.7668 629.6 0.9660
    122.6 2.2 1.6478 0.7990 627.8 0.9635
    121.1 2.1 1.6478 0.8310 625.9 0.9610
    119.6 2.0 1.6478 0.8656 624.0 0.9584
    117.9 1.9 1.6478 0.9090 621.8 0.9555
    116.3 1.8 1.6478 0.9520 619.7 0.9525
    114.5 1.7 1.6478 0.9988 617.4 0.9495
    112.6 1.6 1.6478 1.0580 614.9 0.9463
    110.7 1.5 1.6478 1.1167 612.5 0.9430
    108.7 1.4 1.6478 1.1890 609.7 0.9395
    106.5 1.3 1.6478 1.2696 606.9 0.9357
    104.2 1.2 1.6478 1.3602 603.8 0.9318
    101.7 1.1 1.6478 1.4725 600.5 0.9275
    99.0 1.0 1.6478 1.5992 597.0 0.9229


  5. 湿り蒸気の断熱的な流れにおける流速ｃ、消費量G、断面径ｄの計算結果
    　表35-1　過熱蒸気の断熱変化計算結果と（19.6）式から流速ｃが計算できます。さらに（19.9）式から消費量Gを計算します。
    　また連続条件から、消費量Gが一定となる断面径ｄを求めます。計算結果を表35-2に示します。

    表35-2　湿り蒸気の断熱的な流れにおける流速ｃ、消費量G、断面径ｄの計算結果
    温度 圧力 エントロピ 比容積 エンタルピ 乾き度ｘ 流速ｃ 消費量G 断面径d
    ℃ ata(kp/cm2） kcal/kg・deg m3/kg kcal/kg 無次元 m/s kg/s m
    142.9 4.0 1.6478 0.4727 653.2 1.0000 0.00 0.00000 ー
    141.9 3.9 1.6478 0.4833 652.1 0.9984 96.99 0.01576 0.01700
    141.0 3.8 1.6478 0.4938 651.0 0.9969 137.29 0.02183 0.01445
    140.1 3.7 1.6478 0.5043 649.8 0.9953 168.29 0.02621 0.01319
    139.1 3.6 1.6478 0.5176 648.6 0.9935 196.57 0.02982 0.01236
    138.1 3.5 1.6478 0.5314 647.4 0.9916 221.67 0.03276 0.01179
    137.1 3.4 1.6478 0.5451 646.1 0.9897 244.29 0.03520 0.01138
    136.1 3.3 1.6478 0.5588 644.8 0.9878 265.07 0.03726 0.01106
    135.1 3.2 1.6478 0.5724 643.6 0.9859 284.41 0.03903 0.01081
    133.9 3.1 1.6478 0.5902 642.2 0.9839 304.46 0.04052 0.01061
    132.8 3.0 1.6478 0.6083 640.7 0.9818 323.50 0.04177 0.01045
    131.7 2.9 1.6478 0.6263 639.3 0.9797 341.56 0.04283 0.01031
    130.5 2.8 1.6478 0.6443 637.9 0.9776 358.78 0.04374 0.01021
    129.3 2.7 1.6478 0.6656 636.3 0.9754 376.41 0.04442 0.01013
    128.0 2.6 1.6478 0.6896 634.7 0.9731 394.21 0.04489 0.01007
    126.7 2.5 1.6478 0.7135 633.0 0.9708 411.32 0.04527 0.01003
    125.4 2.4 1.6478 0.7373 631.4 0.9685 427.83 0.04557 0.01000
    124.0 2.3 1.6478 0.7668 629.6 0.9660 444.89 0.04557 0.01000
    122.6 2.2 1.6478 0.7990 627.8 0.9635 461.93 0.04541 0.01002
    121.1 2.1 1.6478 0.8310 625.9 0.9610 478.46 0.04522 0.01004
    119.6 2.0 1.6478 0.8656 624.0 0.9584 495.09 0.04492 0.01007
    117.9 1.9 1.6478 0.9090 621.8 0.9555 512.93 0.04432 0.01014
    116.3 1.8 1.6478 0.9520 619.7 0.9525 530.28 0.04375 0.01021
    114.5 1.7 1.6478 0.9988 617.4 0.9495 547.70 0.04307 0.01029
    112.6 1.6 1.6478 1.0580 614.9 0.9463 566.29 0.04204 0.01041
    110.7 1.5 1.6478 1.1167 612.5 0.9430 584.42 0.04110 0.01053
    108.7 1.4 1.6478 1.1890 609.7 0.9395 603.57 0.03987 0.01069
    106.5 1.3 1.6478 1.2696 606.9 0.9357 623.19 0.03855 0.01087
    104.2 1.2 1.6478 1.3602 603.8 0.9318 643.24 0.03714 0.01108
    101.7 1.1 1.6478 1.4725 600.5 0.9275 664.66 0.03545 0.01134
    99.0 1.0 1.6478 1.5992 597.0 0.9229 686.63 0.03372 0.01162

    　表35-2から、消費量の最大値は0.04557kg/sであり、このときの圧力は約pcr=2.3ata(kp/cm2)、流速は約ccr＝445m/sとな ることがわかります。
    　また連続条件から、ノズルの断面径は圧力は約pcr=2.3ataの点で最小となり、末広がりの形状となることがわかります。


  6. 理想気体の断熱的な流れにおける臨界圧力ｐｃｒと臨界流速ｃｃｒの計算
    　理想気体の臨界圧力ｐｃｒを与える式は

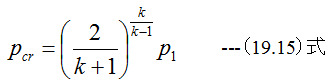
    であり、ｋ＝1.135、p1=4ataとすると

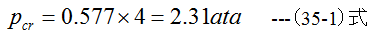
    となり、表34-2の計算結果とほぼ一致します。また理想気体の臨界流速を与える式は

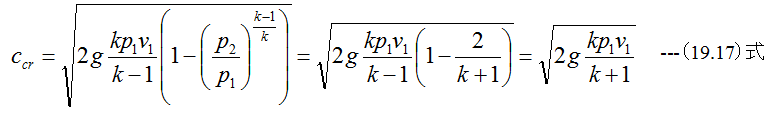
    であり、k=1.135、p1=4ata、v1=0.4727m3/kgとすると

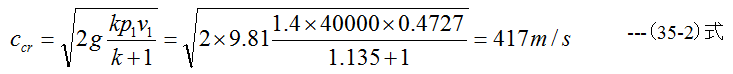
    　となり、表34-2の計算結果ccr=445m/sとは誤差が発生します。この結果から、湿り蒸気の断熱的な流れは理 想気体の計算式が適用しにくいことがわかります。








３６章：飽和蒸気のカルノーサイクルに行く。

トップページに戻る。