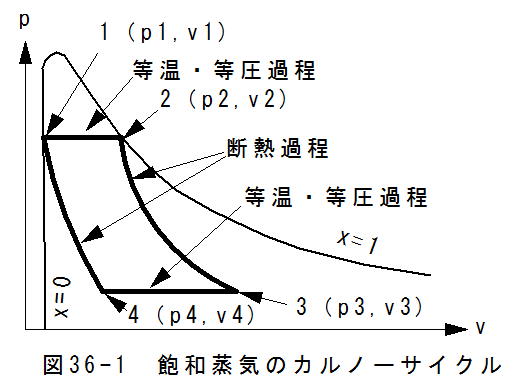
飽和蒸気のカルノーサイクル説明図を図36-1に示します。
11章では、理想気体でのカルノーサイクルについて検討しましたが、ここでは飽和蒸気における カルノーサイクルについて検討します。
図36-1において、1点から2点の過程がボイラーによる等温・等圧の加熱過程、2点から3点の過程が蒸気機 関のシリンダーによる断熱膨張過程、3点から4点の過程が復水器による等温・等圧の冷却過程、4点から1点 が圧縮器による断熱圧縮過程に対応します。
図36-1の1点から2点がボイラーによる等温・等圧の加熱過程です。この過程は等温・等圧のまま、熱量が加わって、水が蒸 発して湿り蒸気の乾き度xが0から1まで変化する過程です。
等温過程の関係式として
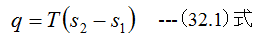
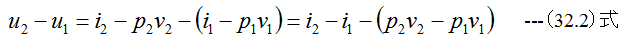
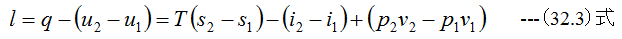
が成立するはずです。
また等圧過程の関係式として
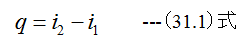
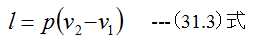
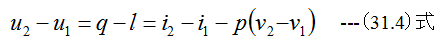
が成立するはずです。
図36-1の2点から3点が蒸気機関のシリンダーによる断熱膨張過程です。
断熱膨張過程の関係式として
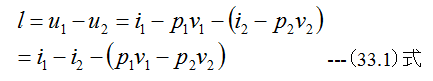
が成立します。
図36-1の3点から4点が復水器による等温・等圧の冷却過程です。この過程は等温・等圧のまま、熱量が奪われ湿り蒸気 の乾き度xが変化する過程です。
ボイラー過程と同じ関係式が成立します。
図36-1の4点から1点が圧縮器による断熱圧縮過程です。
シリンダーによる断熱膨張過程とおなじ関係式が成立します。
図36-1の1点から2点がボイラーによる等温・等圧の加熱過程で受取る熱量は、 1点における温度をT1、エント ロピをs1、2点における温度をT1、エントロピをs2とすると
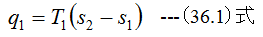
図36-1の3点から4点が復水器による等温・等圧の冷却過程で3点のエントロピはs2等しく、4点のエントロピはs1と等しくなります。
3点の温度をT2とすると3点から4点の過程で放出する熱量は
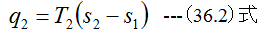
サイクルの熱効率は
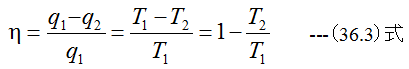
となります。
11章では、理想気体でのカルノーサイクルの効率は
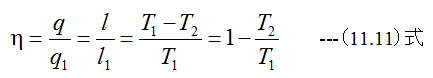
であり、 (35.3)式と(11.11)式は同一であることを意味します。
低温側温度を40℃とした場合の効率を表36-1に示します。
表36-1 飽和蒸気のカルノーサイクルの効率
| 高温側(℃) | η |
| 150 | 0.26 |
| 200 | 0.34 |
| 250 | 0.40 |
| 300 | 0.45 |
| 350 | 0.50 |
| 400 | 0.54 |
| 450 | 0.57 |
| 500 | 0.60 |
| 550 | 0.62 |
| 600 | 0.64 |
| 650 | 0.66 |
| 700 | 0.68 |
| 750 | 0.69 |
| 800 | 0.71 |
| 850 | 0.72 |
| 900 | 0.73 |
表36-1の冷却温度は40℃としました。このときの圧力は0.075ataであり、負圧になります。
表36-1から、高温側の温度を上げるほど効率が向上することがわかります。
しかし飽和蒸気が存在する臨界温度は374℃であり、これ以上の温度では飽和蒸気は存在できずに過熱蒸気となります。
飽和蒸気で達成可能な効率には限界があるということになります。
図36-1においてp1=100ata、p3=0.1ataとした場合の各点での温度、圧力、乾き度,、比容積、エンタルピ、総熱量、内部エネルギ、エントロピを求めよ。
また、膨張の仕事、圧縮の仕事、効率を求めよ。
解答
各点での温度、圧力、乾き度,、比容積、エンタルピ、総熱量、内部エネルギ、エントロピはワークブック「湿り蒸気表.xls 」から
表36-2 各点での温度、圧力、乾き度,、比容積、エンタルピ、総熱量、内部エネルギ、エントロピ
| サイクル | 圧力 | 温度 | 乾き度 | 比容積 | エンタルピ | 総熱量 | 内部エネルギ | エントロピ |
| 点 | kp/cm2 | ℃ | x | vx(m3/kg) | ix(kcal/kg) | λ’’(kcal/kg) | ux(kcal/kg) | sx(kcal/kg・deg) |
| 1 | 100.0 | 309.5 | 0.00 | 0.00145 | 333.9 | 330.6 | 330.6 | 0.7970 |
| 2 | 100.0 | 309.5 | 1.00 | 0.01845 | 651.1 | 647.7 | 607.9 | 1.3410 |
| 3 | 0.1 | 45.4 | 0.66 | 9.93088 | 423.4 | 423.4 | 400.2 | 1.3410 |
| 4 | 0.1 | 45.4 | 0.36 | 5.37744 | 250.0 | 250.0 | 237.5 | 0.7966 |
となります。
効率は
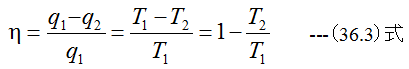
(35.3)式から求めることになります。
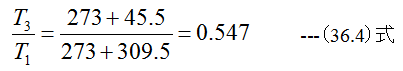
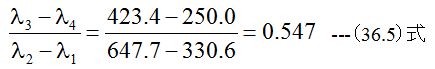
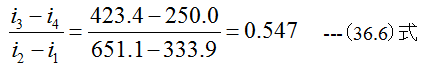
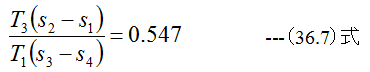
となりどの計算方法でも
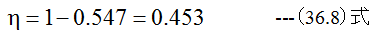
となります。
あるいは、仕事からも効率を求めることができます。
1点と2点間の仕事l1は
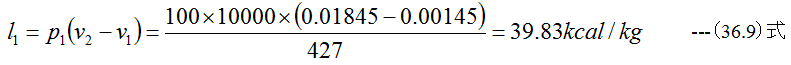
2点と3点間の仕事l2は
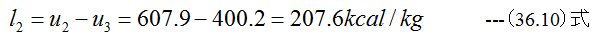
3点と4点間の仕事l3は
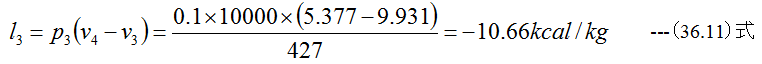
4点と1点間の仕事l4は
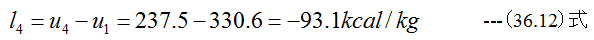
合計の仕事lは
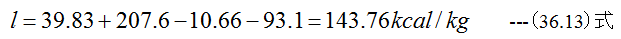
効率は
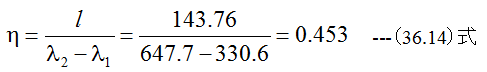
となります。このようにさまざまな計算方法で同じ値になるのは、飽 和蒸気のカルノーサイクルの特徴ですが一般サイクルに適用できるわけではありません。