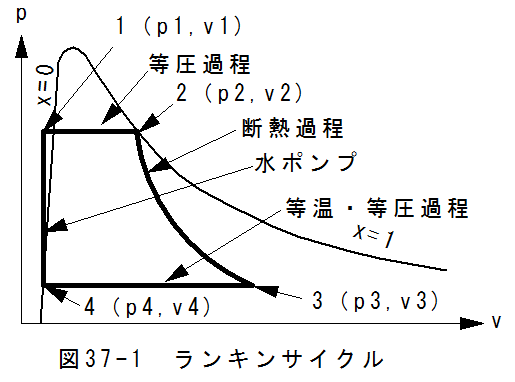
飽和蒸気のランキンサイクル３６章の飽和蒸気のカルノーサイクルでは、圧縮機を必要としますが、ランキンサイクルでは圧縮機を水ポンプに置き換えるため、小型化できます。 飽和蒸気のランキンサイクル説明図を図37-1に示します。
図37-1において、1点から2点の過程がボイラーによる等圧の加熱過程、2点から3点の過程が蒸気機関のシリンダーによる断熱膨張過程、3点から4点の過 程が復水器による等温・等圧の冷却過程、4点から1点が水ポンプによる加圧過程に対応します。
ボイラー過程図37-1の1点から2点がボイラーによる等圧の加熱過程です。この過程は等圧のまま、熱量が加わって沸点以下の水が沸点に達します。沸点以後 は水が蒸発して湿り蒸気の乾き度ｘが0から1まで変化する過程です。
1点から2点の過程は(a)沸点以下の水が沸点に達する過程、(b)沸点から飽和蒸気に変化する過程に別れますがともに等圧変化過程です。従っ て以下の関係式が共通して成立します。
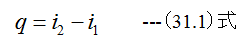
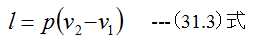
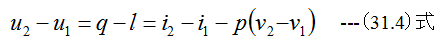
シリンダーによる断熱膨張過程図37-1の2点から3点が蒸気機関のシリンダーによる断熱膨張過程です。
断熱膨張過程の関係式として
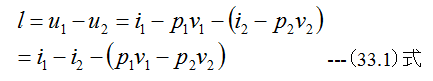
が成立します。
復水器過程図36-1の3点から4点が復水器による等温・等圧の冷却過程です。この過程は等温・等圧のまま、熱量 が奪われ湿り蒸気の乾き度ｘがゼロまで変化する過程です。
等温過程の関係式として
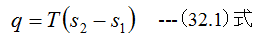
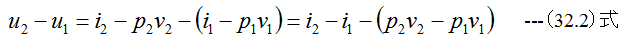
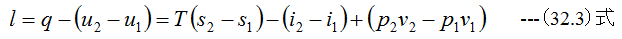
が成立するはずです。
また等圧過程の関係式として
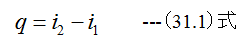
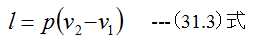
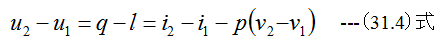
が成立するはずです。
水ポンプ過程図37-1の4点から1点が水ポンプによる加圧過程です。 水の性質は加圧による比容積の変化が小さく無視できます。従って温度、比容積、内部エネルギ、エントロピは変化しないと仮定できます。
エンタルピは
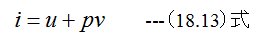
（18.13）式から計算できます。
例題37-1図37-1の飽和蒸気のランキンサイクルにおいてｐ1＝100ata、ｐ3＝0.1ataとした場合の各点での温度、圧力、乾き度,、比容積、エンタルピ、 総熱量、内部エネルギ、エントロピを求めよ。
また、ランキンサイクルの効率を求めよ。
解答
（１）各点の状態
1点の状態は最初には求まりません。2点、3点、4点の順に求め、最後に1点の状態を求めます。
2点、3点、4点の温度、圧力、乾き度,、比容積、エンタルピ、総熱量、内部エネルギ、エントロピはワークブック「湿り蒸気表.xls 」から
表37-1 2点、3点、4点の温度、圧力、乾き度,、比容積、エンタルピ、総熱量、内部エネルギ、エントロピ
| サイクル | 圧力 | 温度 | 乾き度 | 比容積 | エンタルピ | 総熱量 | 内部エネルギ | エントロピ |
| 点 | kp/cm2 | ℃ | ｘ | vx（m3/kg) | ix（kcal/kg） | λ’’(kcal/kg) | ux（kcal/kg） | sx(kcal/kg・deg) |
| 2 | 100.0 | 309.5 | 1.00 | 0.01845 | 651.1 | 647.7 | 607.9 | 1.3410 |
| 3 | 0.1 | 45.4 | 0.66 | 9.93088 | 423.4 | 423.4 | 400.2 | 1.3410 |
| 4 | 0.1 | 45.4 | 0.00 | 0.00101 | 45.4 | 45.4 | 45.4 | 0.1540 |
1点のエンタルピはｖ0を0℃の比容積として
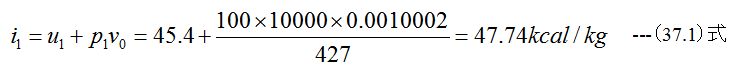
となります。
（２）1点から2点での熱量ｑ1
（31.1）式から
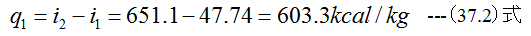
となります。
（３）3点から4点での熱量ｑ3
（31.1）式から
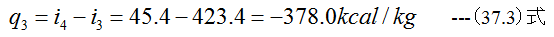
（４）ランキンサイクルの効率
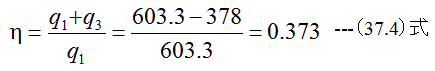
となります。カルノーサイクルと比較してランキンサイクルの理論効率は少し劣りますが、圧縮機 が不要となるため圧縮機での損失がなく小型になります。このため、ほとんどの蒸気機関では、ランキン サイクルが使用されます。
３８章：湿り空気に行く。