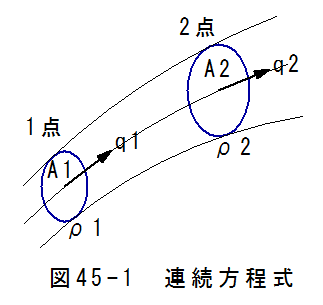
連続方程式連続の条件については、１８章：気体の流れによる仕事で述べていますので追加事項はありません。
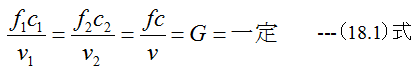
（18.1）式においては、ｆが面積、ｃが流速、ｖが比容積、Gが流量を表しています。図45-1の連続方程式も意味は同じですが記号が変わっています。
図45-1においてはAが面積、qが流速、ρが比質量（密度）、Gが単位時間の質量の流量です。（18.1）式を書き直すと
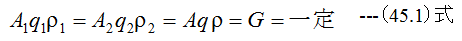
（18.1）式と（45.1）式は全く同じことを意味しています。分野により使用する記号が異なりますので注意が必要です。
運動方程式とベルヌーイの定理ニュートンの運動の第2法則によれば、質量mの物体に外力ｆが作用したとき
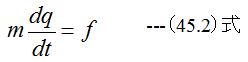
（45.2）式を満足する加速度dq/dtが発生します。
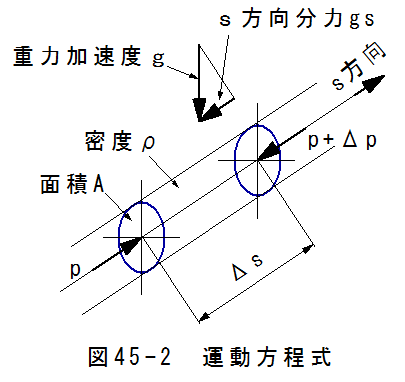
図45-2は流体に作用する力のバランスを示しています。図45-2において流れの方向をｓとしています。S方向に垂直な面積がAであり、 ρが比質量です。Δｓだけ離れた面に囲まれた流体の質量は
となります。質量ｍに作用する力は
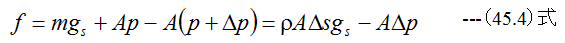
（45.2）式に（45.3）式と（45.4）式を代入すると
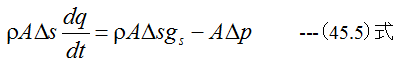
（45.5）式の両辺をρAΔｓで割って、Δｐ/Δｓの極限を∂p/∂sとすれば
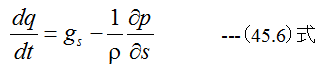
ここで
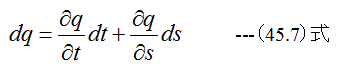
（45.7）式の両辺をdtで割ると
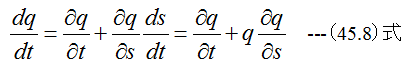
となります。ここで速度が時間的に変化しない定常流れにおいては
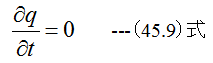
となります。したがって
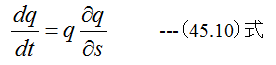
（45.6）式に（45.10）式を代入すると
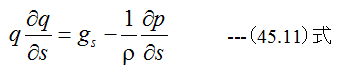
定常流れにおいては、 ∂q/∂t=0、 ∂q/∂s=dq/ds、∂p/∂s=dp/dsとなります。したがって
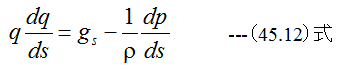
となります。 （45.12）式を変形すると
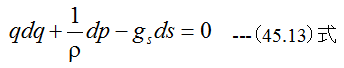
ここで重力方向を-ｙとした場合
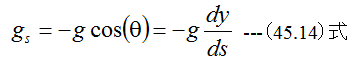
（45.13）式に（45.14）式を代入して
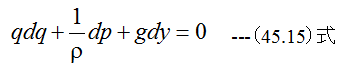
（45.15）式においてqdqは単位質量あたりの運動エネルギーの増加分、dp/ρは圧力エネルギーの増加分、 ｇｄｙは位置ポテンシャルエネルギーの増加分です。
単位質量あたりの運動エネルギー、圧力エネルギー、位置ポテンシャルエネルギーの増加分の総和 はゼロとなります。
q1、ｐ1、y1を初期値として（45.15）式を積分すると
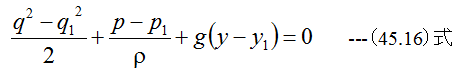
（45.16）式から、流速q、圧力ｐ、位置ｙのうち2個のパラメータの値が決定すると残り1個のパラ メータの値が決定することがわかります。
（45.15）式および（45.16）式をベルヌーイの定理ともいいます。
例題45-1（45.16）式においてｑ1＝ｙ1＝0、p-p1=0としたとき流速qと位置ｙの関係をグラフにせよ。
解答：
（45.16）式にｑ1＝ｙ1＝0、p-p1=0を代入すると
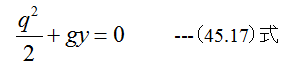
従って
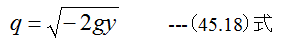
（45.18）式の計算が可能な条件はｙがマイナスである必要があります。
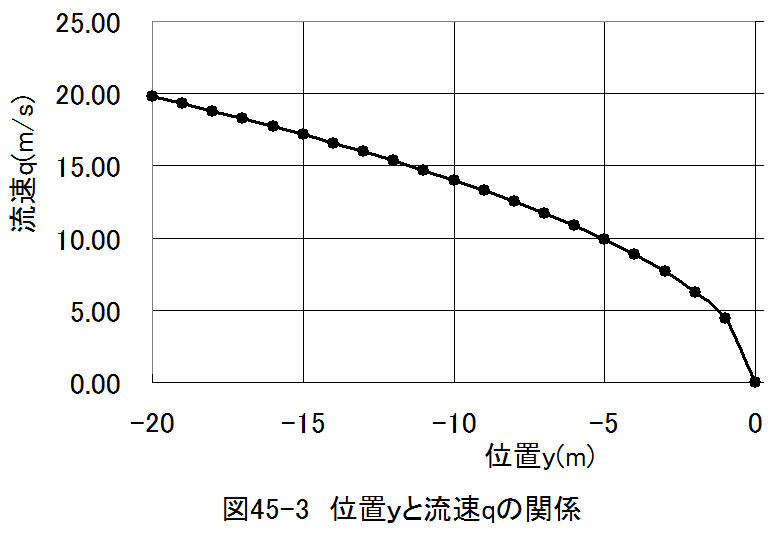
例題45-1はダムの底から流れだす水の流速に相当します。図45-3から落差20mのダムの底から流れ出す水の流速は 約20m/s近くに達することがわかります。
しかし、この結果は粘性抵抗の無い理想流体を前提としているため実際とは誤差を生じます。
例題45-2（45.16）式においてｑ1＝0、y-ｙ1=0、Δｐ＝p-p1としたとき流速qと圧力Δｐの関係をグラフにせよ。
解答：
（45.16）式にｑ1＝0、y-y1=0、Δｐ＝p-p1を代入すると
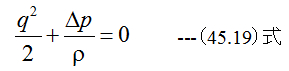
従って
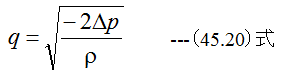
（45.20）式の計算が可能な条件はΔｐがマイナスである必要があります。
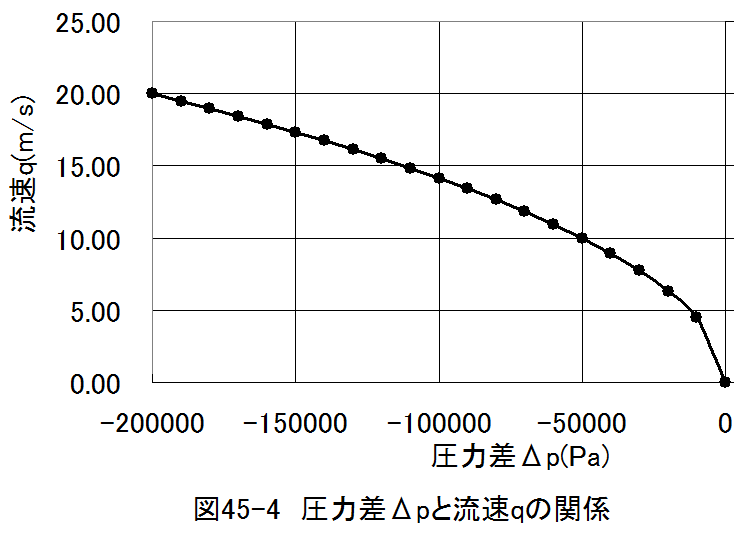
例題45-2は圧力差と流速の関係を表しており、ピトー管等の流速測定に応用できます。図45-4から圧力 差0.2MPa（約2気圧）で流速は20m/sになることがわかります。
しかし、この結果は粘性抵抗の無い理想流体を前提としているため実際とは誤差を生じます。
４６章：エネルギー変化を伴う流体のエネルギー方程式に行く。