非定常流れのエネルギー方程式
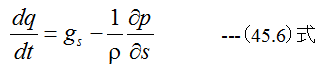
（45.6）式に
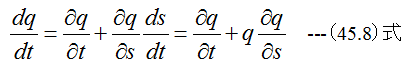
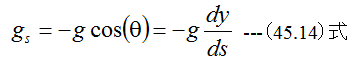
（45.8）式と（45.14）式を代入すると
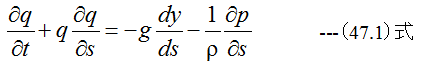
（47.1）式を流れの道程ｓにそって積分すると
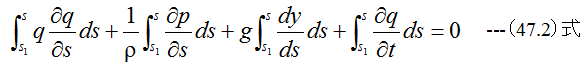
となります。ここで
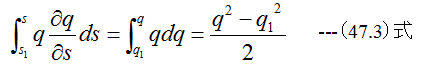
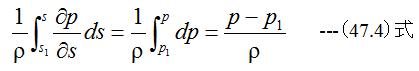
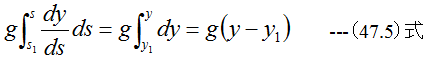
（47.2）式に（47.3）式、 （47.4）式、 （47.5）式を代入すると
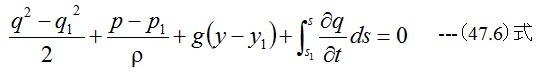
となります。また圧力損失Δpがある場合は
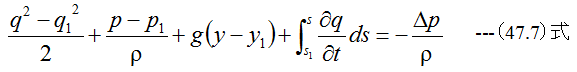
となります。 （47.6）式は∂q/∂tの項があるため、時間ｔの変化に伴いネネルギーバラン スが変化することを示しています。
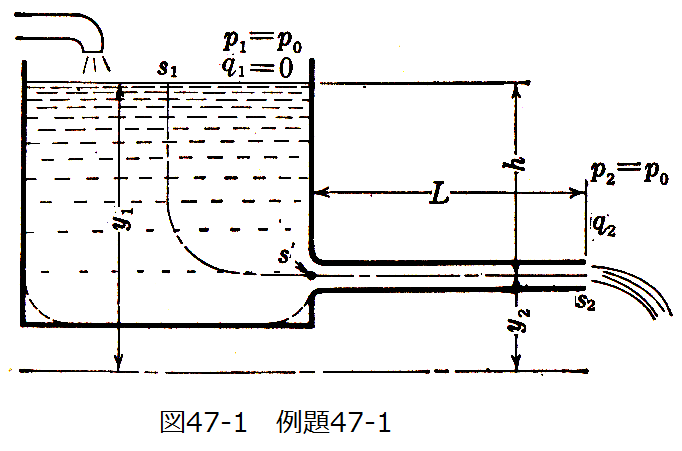
例題47-1図47-1のように容器に取付けた管の一端を急に開いた場合、ここより出る水の速度はどの様に変化 するか？ただし容器には水を補充して一定に保つこととし、管摩擦は無いとする。
解答
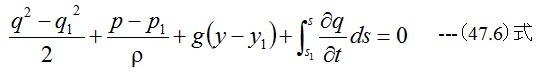
（47.6）式において、q1=0、p-p1=0、y-y1=-hとすれば
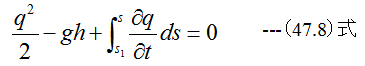
となります。 （47.8）式の時間変化の項は、水面ｓ1から管の入り口s’までは、断面積が大きく流速qは近 似的にゼロとできます。
また管の入り口s’から管の出口s2までは断面積が等しいため流速qは一定となります。したがって
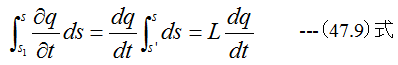
（47.8）式に（47.9）式を代入すると
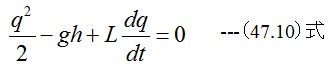
となります。ここで時間t=∞においてdq/dt＝0とするならば
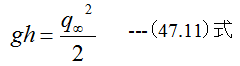
（47.10）式に（47.11）式を代入すると
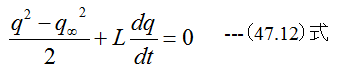
（47.12）式を変形すると
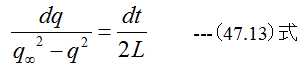
（47.13）式を積分して
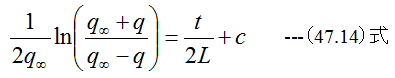
（47.14）式のｃは積分定数ですが、t=0でq=0の初期条件を代入するとc=0となります。従って
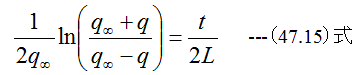
（47.15）式を変形すると
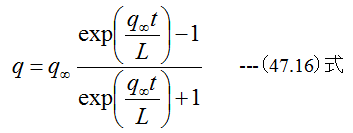
となります。
重力加速度 g＝9.81（m/s2）
落差 ｈ=10(m)
とすると
定常流速 q∞=14.01(m/s2)
となります。
管長さLが5m、10m、20mの場合について、計算した結果を図47-2に示します。
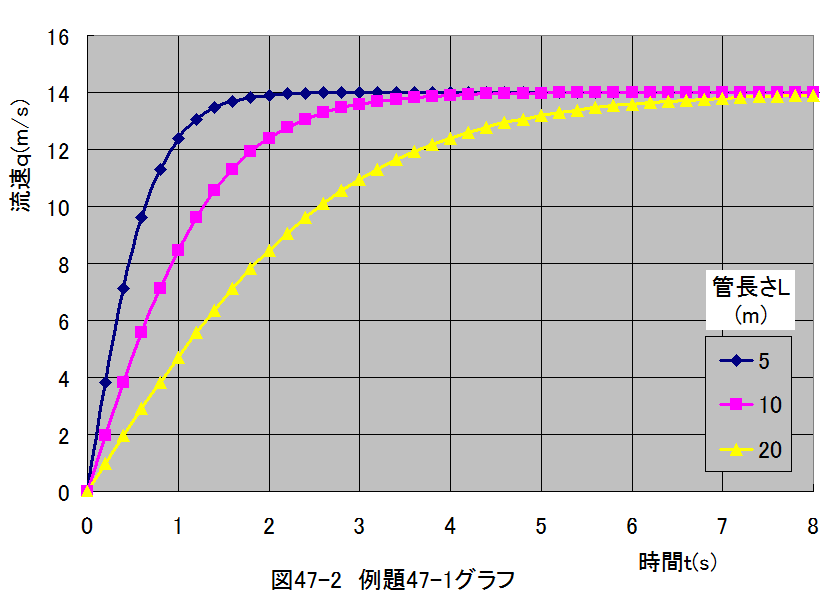
図47-2から、管長さLが長くなると応答が遅くなることがわかります。
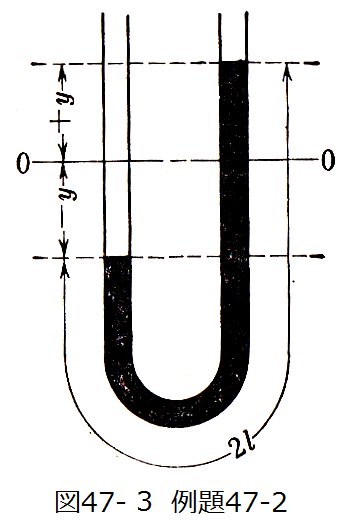
例題47-2図47-3に示すように両端を開いたU字管に液をいれて、基準平面0-0に対して、最初両端に-ｙ、+ｙの水 位の差をつけると、管内の水は振動する。この振動の周期を求めよ。ただし、液体は理想流体とし、U字管 の液の全長を2ｌとする。
解答
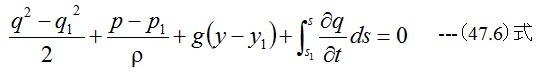
（47.6）式において、q＝q1、p-p1=0、y=-y1とすれば
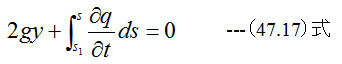
となります。またU字管内の液体はsに無関係に同一流速であるため
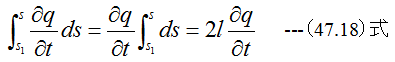
となります。また
の関係があります。 （47.17）式に（47.18）式と（47.19）式を代入すると
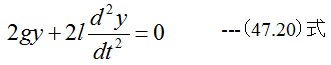
変形して
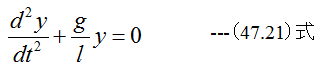
（47.21）式の一般解は
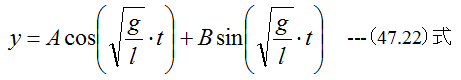
となります。周期Tは
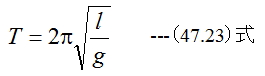
となります。
（47.23）式の計算結果をグラフにすると図47-4に示すようになります。
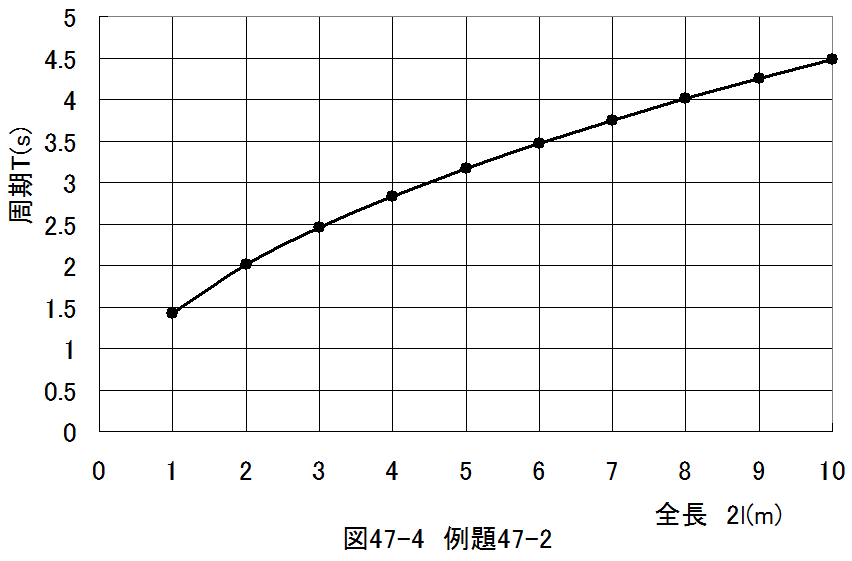
図47-4からU字の液の全長2ｌが大きくなると周期Tが長くなることがわかります。
４８章：運動量の法則に行く。