質点の運動量の法則ニュートンの運動の第2法則によれば
力＝質量×加速度
すなわち
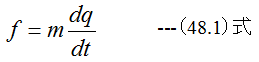
となるが、これを一般化すると
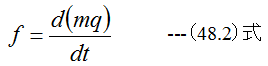
となる。 （48.2）式は次のように記述できる。「物体に作用した力は、その物体の運動量の単位時間あたりの変化に等しい。」
力のバランスを考えると（48.2）式は下記のようになる。
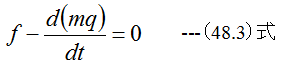
（48.3）式は次のように記述できる。「物体の運動量の単位時間あたりの変化は逆方向に反力を生じ、物体に作用した力を打ち消す。」
（48.1）式、 （48.2）式、 （48.3）式は数学的には同じですが、解釈については微妙な差があります。また、力と 加速度と運動量は方向と大きさを持つ３次元ベクトルです。したがって、ｘ成分、y成分、z成分に分けて考えるのが正式です。
これに対して、エネルギーは方向を持たないスカラー量であるため、エネルギー方程式と力のバランス方程式は扱い方が異なってきます。
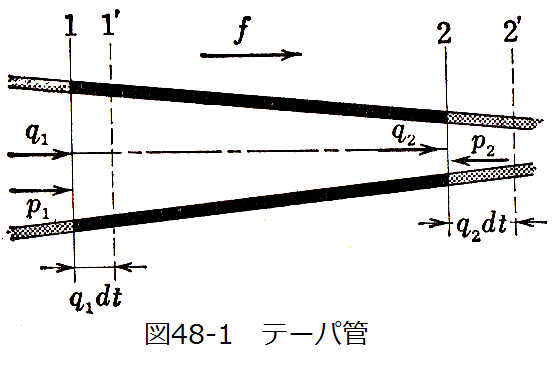
テーパ管の流れにおける運動量の法則図48-1に示すようにまっすぐなテーパ管の流れにおいて断面1と断面2の間の流体に着目する。この流体に流れの方向に一定の力ｆが作用した 場合、dt時間後には断面1‘と断面2’の間に移動する。この時の運動量の変化は
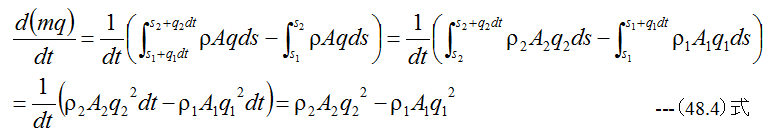
となります。ここで
（48.4）式に（48.5）式と（48.6）式を代入すると
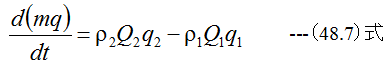
一方、圧力による力は
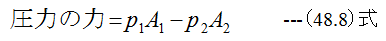
また流体が管に作用による力をFとした場合
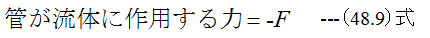
従って力のバランス方程式は
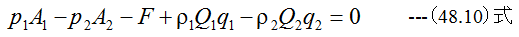
となります。また
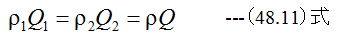
が成立する場合は
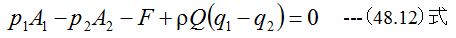
となります。変形すると
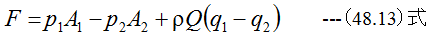
ここで（48.13）式は流体が管に作用による力と管が流体に作用する力は大きさが等しく、方向 が反対となることに注意する必要があります。
すなわち、管は流体の運動によりFの力を受けることになります。
断面積一定直管の流れにおける運動量の法則図48-2に示すように断面積Aが一定の直管内を流体が一定速度qで1から2の方向に流れている。
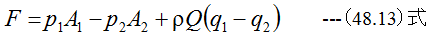
（48.13）式において、q1＝q2、A1=A2=Aとなります。したがって
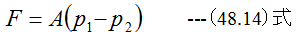
となります。したがって粘性流体の場合は摩擦損失により圧力の低下が発生します。断面積Aが一定の直 管は流れの方向にFの力を受けます。
逆に粘性流体は断面積Aが一定の直管から流れと反対方向にFの力を受けます。
摩擦損失の無い理想流体においてはp1=p2、F=0となります。
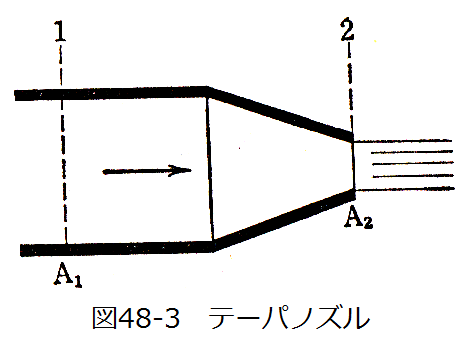
テーパノズルにおける運動量の法則図48-3に示すように、液体がテーパノズルから大気中に流量Qの割合で噴出している。
運動量の法則は
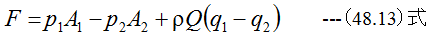
となります。ここで
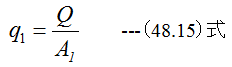
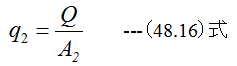
の関係があります。また圧力の基準を大気圧とすれば
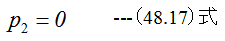
です。またベルヌーイの方程式
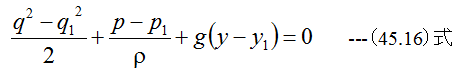
（45.16）式においてｙ-ｙ1＝0となります。変形すると
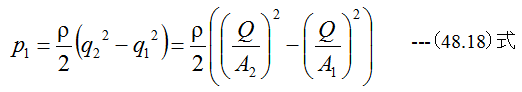
（48.13）式に（48.15）式、 （48.16）式、 （48.18）式を代入すると
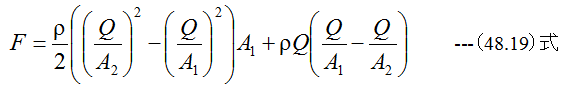
整理すると
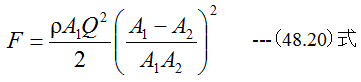
となります。
流体からノズルが受ける力Fは（48.20）式から、A1＝A2のときゼロとなり、A1とA2の差が大きいと き大きくなることがわかります。
また、流体の慣性力はノズルに対して流れと反対方向に作用するはずですが、流体からノズルが受 ける力Fは常に流れの方向となります。これは圧力の影響が支配的であると解釈できます。
４９章：曲管の流れにおける運動量の法則に行く。