曲管の流れ
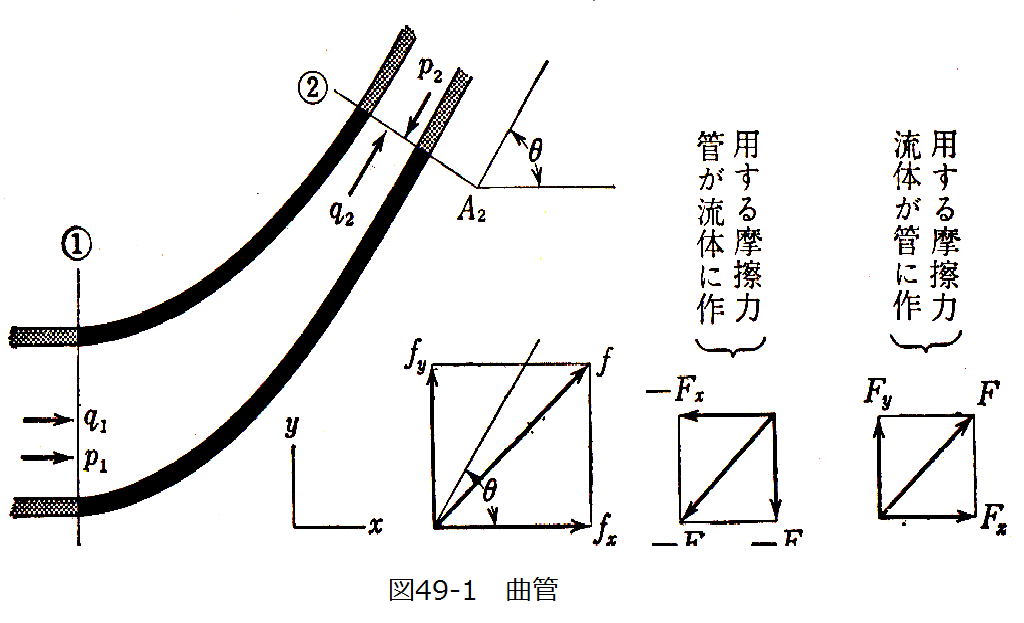
図49-1は曲管内を流体が流れている場合を示す。管の上流1、下流2における流速をq1、q2；断面積をA1、A2とする。
運動量の法則
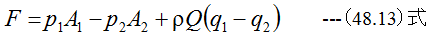
はｘ成分とy成分に分けて考える必要があります。
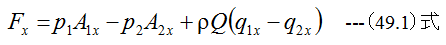
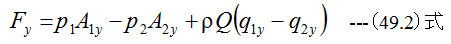
ここで
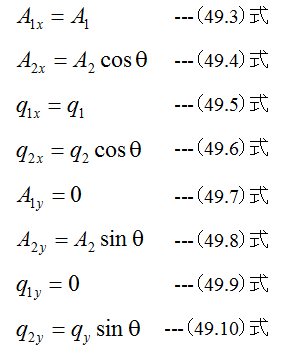
（49.1）式と（49.2）式に（49.3）式〜 （49.10）式を代入すると
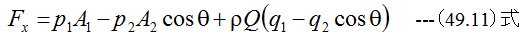
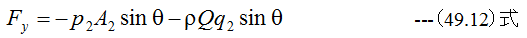
となります。 （49.12）式から曲管はy軸に関してマイナス方向の力を受けることがわかります。
例題49-1
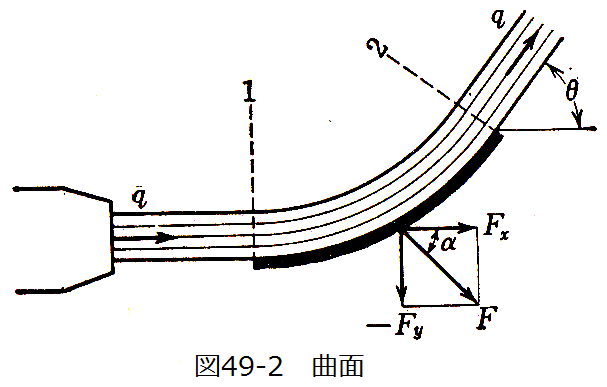
図49-2に示すように、断面積Aのノズルより速度qにて噴出する流体が固定局面にそって速度を変えることなく方向がθだけ変えられた。
この場合に固定局面に作用する力を求めよ。
解答
曲管の流れにおける運動量の法則から
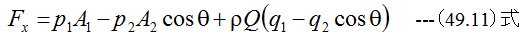
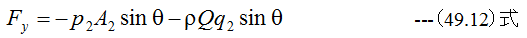
（49.11）式と（49.12）式においてp1=p2=0、q1=q2=q、A1=A2=Aとなります。したがって
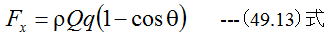
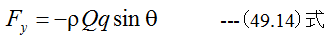
となります。
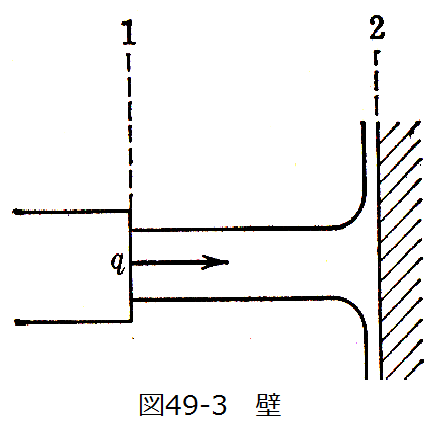
壁面に衝突する噴流図49-3に示すように、流量Q、比質量ρなる噴流がqなる速度で噴出し、これに垂直に置かれた平面に当たる場合、噴流が板に作用する力Fを求めます。
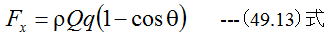
（48.13）式において、p1=p2=0、q1=q、ｑ2＝0となります。したがって
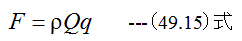
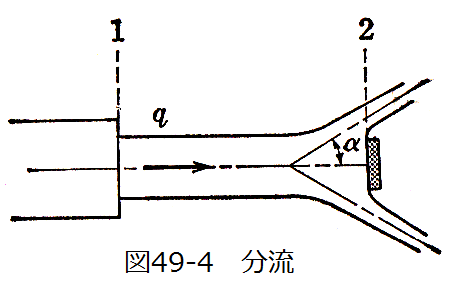
例題49-2図49-4に示すように、流量Qなる噴流が小さな円板に当たり、噴流とαなる角度で流れ出る場合、流体が円板に作用する力 を求めよ。ただし噴流の比質量をρ、速度をqとする。
解答
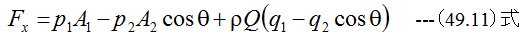
（49.11）式において、Fx=F、p1=p2=0、q1=q2=q、θ=αとなります。したがって
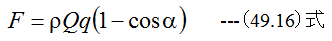
となります。
５０章：噴流による推進理論に行く。