プロペラの理論
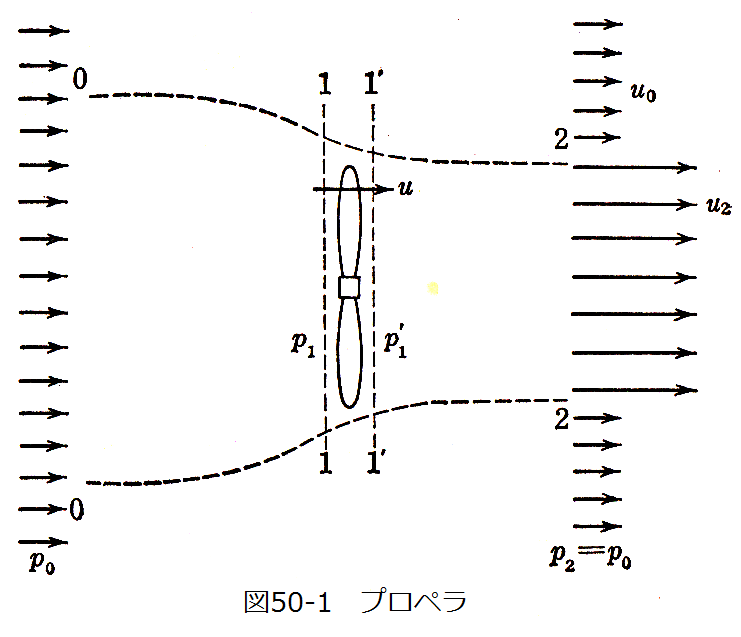
図50-1に示すように、流速u0の一様な流体中にプロペラが固定され、後方2-2では、プロペラの回転により流速u2になる とする。この状態は静止流体中をプロペラが左方向にu0の速度で進行し、プロペラ後方の流速がu2-u0の場合と同じである。
圧力は0-0位置で大気圧であり、プロペラ直前1-1で減少し、プロペラ直後1‘-1’で増加し、2-2位置でふたたび大気圧になる。
流体がプロペラに作用する力Fは
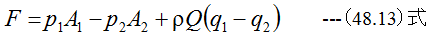
（48.13）式において、p1=p2=0、q1=u0、q2=u2となります。したがって
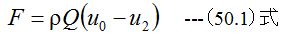
となります。またプロペラのところにおける流速をu、断面積をAとすると
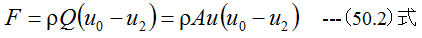
となります。推力Fプロペラ前後での圧力差の条件を満足する必要があります。
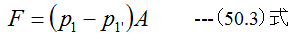
またベルヌーイの式を満足する必要があります。
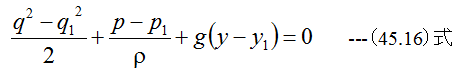
（45.16）式を0-0と1-1間と1‘-1’と2-2間に適用すると
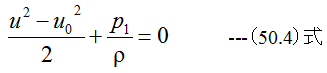
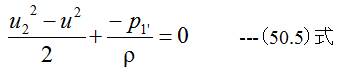
となります。 （50.2）式、 （50.3）式、 （50.4）式、 （50.5）式の条件式から
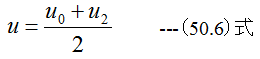
（50.6）式の関係式を得ることができます。
単位時間当たりのエネルギーすなわち有効仕事率Peは推力Fの方向を考慮して
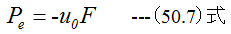
（50.7）式に（50.1）式を代入すると
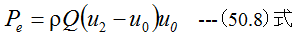
となります。また速度u0をu2に加速するに要する仕事率Piは
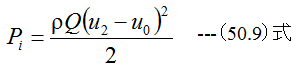
となります。したがってプロペラの理論効率ηは
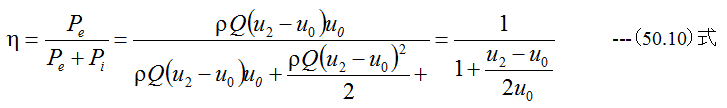
となり、u2-u0を小さくすると効率が向上することがわかります。
例題50-1気圧100kPa、温度20℃、相対湿度50%の空気の比質量は1.183kg/m3となります。この空中を毎時400km/h で飛んでいる航空機において、直径2.1mのプロペラ1基より放出される空気の流量は465m3/sである。
この時のプロペラの推力、動力、効率を求めよ。
解答
飛行速度は
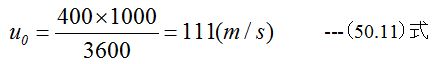
プロペラにおける流速uは
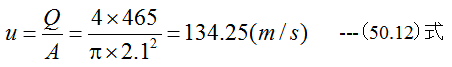
プロペラ後方の速度u2は（50.6）式から
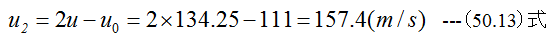
推力は（50.1）式から
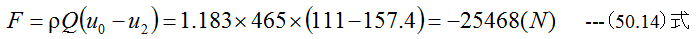
（50.14）式のマイナスは推力が流れと反対方向を意味します。有効動力は（50.7）式から
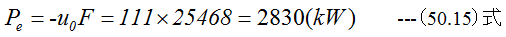
となります。効率は（50.10）式から
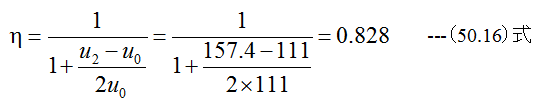
となります。
ジェットの理論
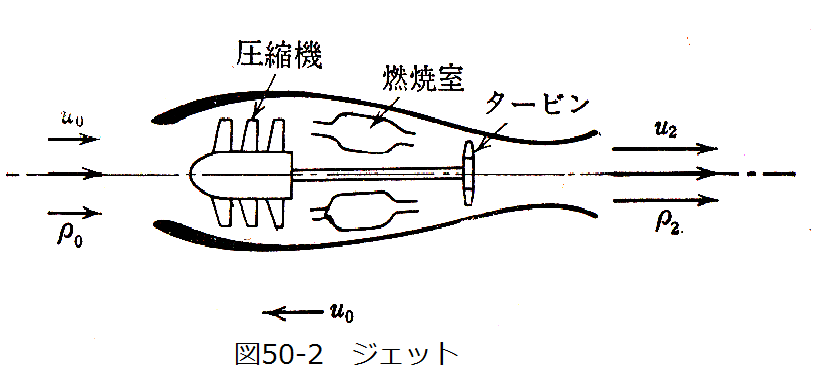
図50-2にターボジェット略図を示します。入口から吸込まれた空気を圧縮機で圧縮し、燃焼室でこれに燃料 を混入して燃焼させ、高温高圧となったガスを高速ジェットとして噴出させる。なおこのガスは途中でガス タービンを回し圧縮機を駆動する役目も果たします。
高温にて噴出されるガスが本体を押し出す力Fはプロペラ推力と同様に下記式となります。
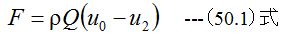
理論効率もプロペラ推力と同様に下記式となります。
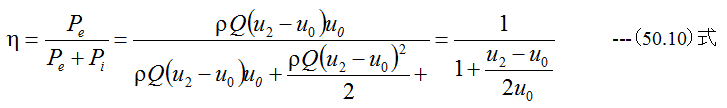
プロペラ推力と同様に、u2-u0を小さくすると効率が向上します。
例題50-2毎時580km/hの速度で飛んでいるジェット機が、高熱のガスを460m/sの速度で直径2mの吐き出し口から噴出し ている。高熱のガスは649℃、圧力1.033kg/cm2でガス定数R=29.27（m・kp/kg・K）とする。
ジェット機の推力を求めよ。
解答
熱力学の基礎方程式から高熱のガスの比質量ρは
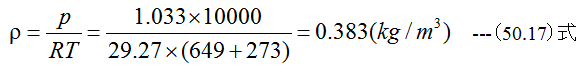
となります。また流量Qは
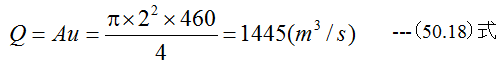
です。飛行速度uは
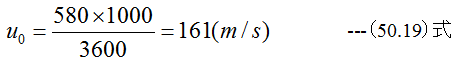
したがって推力Fは
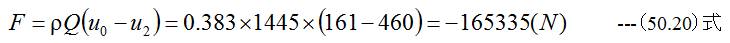
となります。マイナスは推力Fが流れと逆方向を意味します。効率は（50.10）式から
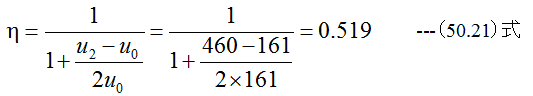
となります。
ロケットの理論
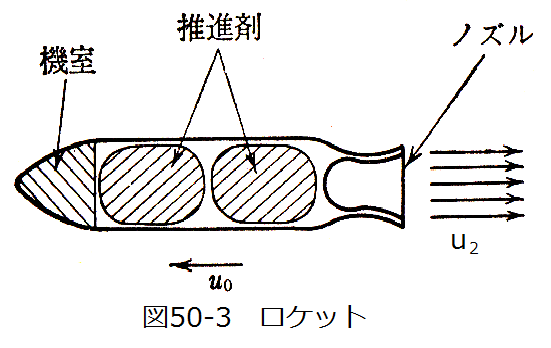
図50-3にロケット略図を示します。ロケットの動力は本体内の推進剤のみにより、大気 中からは空気を取らない構造です。推力Fは
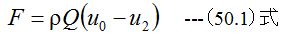
（50.1）式において、u0=0となります。したがって
単位時間当たりのエネルギーすなわち有効仕事率Peは推力Fの方向を考慮して
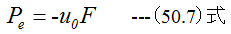
（50.7）式に（50.22）式を代入すると
となります。また速度をu2-u0に加速するに要する仕事率Piは
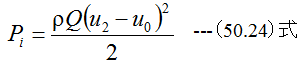
となります。したがってロケットの理論効率ηは
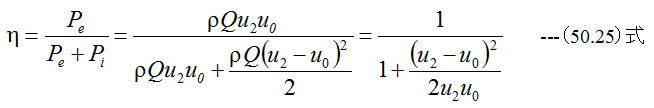
となり、u2-u0を小さくすると効率が向上することがわかります。また推進剤消費量をWとすると
であり、推力Fは
となります。
例題50-3ロケットの推進剤消費量は125kg/s、噴射ガスの速度は2350m/sであった。ロケットの推力を求めよ。
解答
（50.27）式から
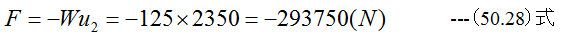
となります。
５１章：運動量モーメントの法則に行く。