質点の運動量モーメント力をｆ、半径をrとしたとき、モーメントMは
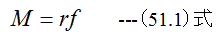
と定義されます。（51.1）式に（48.2）式を代入すると
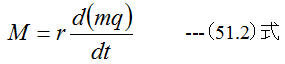
となります。 （51.2）式を一般化すると
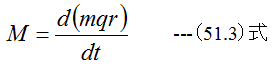
となる。 （51.3）式は次のように記述できる。「物体に作用したモーメントは、その物体の運動量モーメントの 単位時間あたりの変化に等しい。」
モーメントのバランスを考えると（51.3）式は下記のようになる。
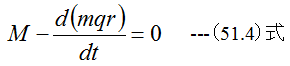
（51.4）式は次のように記述できる。「物体の運動量モーメントの単位時間あたりの変化は逆方向にモーメントを生 じ、物体に作用したモーメントを打ち消す。」
（51.1）式、 （51.2）式、 （51.3）式、 （51.4）式は数学的には同じですが、解釈については微妙な差があ ります。また、モーメントと運動量モーメントは方向と大きさを持つ３次元ベクトルです。したがって、ｘ成分、 y成分、z成分に分けて考えるのが正式です。
流体における運動量モーメントの法則
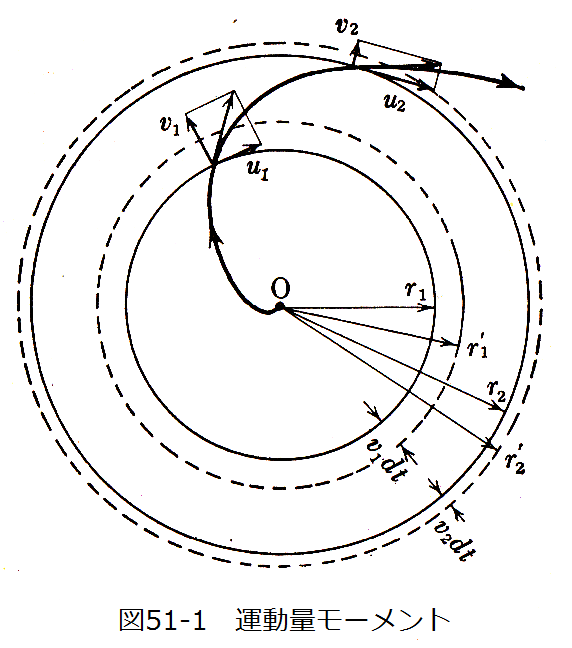
図51-1は原点Oを中心として定常的に旋回しながら流出している流体のモデル図です。
図では厚さ方向を無視していますが実際には厚みがありこれをzとします。
ここで半径r1からｒ2までの運動モーメントMは
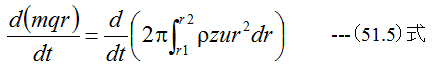
となります。
r1における半径方向流速をv1、円周方向流速をu1、比質量をρ1
r2における半径方向流速をv2、円周方向流速をu2、比質量をρ2
とします。
dｔ時間後のr1の位置r1’は
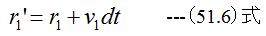
となります。同様にdｔ時間後のr2の位置r2’は
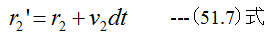
（51.5）式に（51.6）式と（51.7）式を代入すると
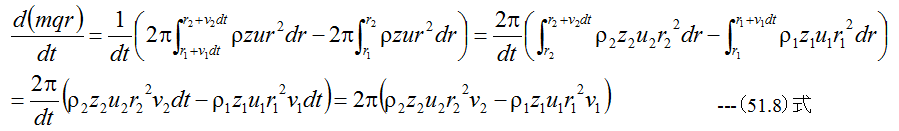
となります。 半径ｒ1における流量をQ1、半径ｒ2における流量をQ2とすれば
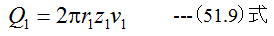
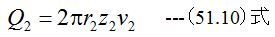
（51.8）式に（51.9）式と（51.10）式を代入すると
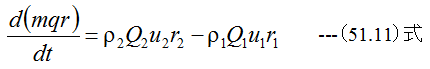
となります。また
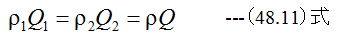
が成立する場合は
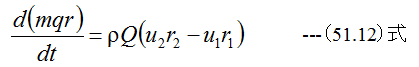
となります。
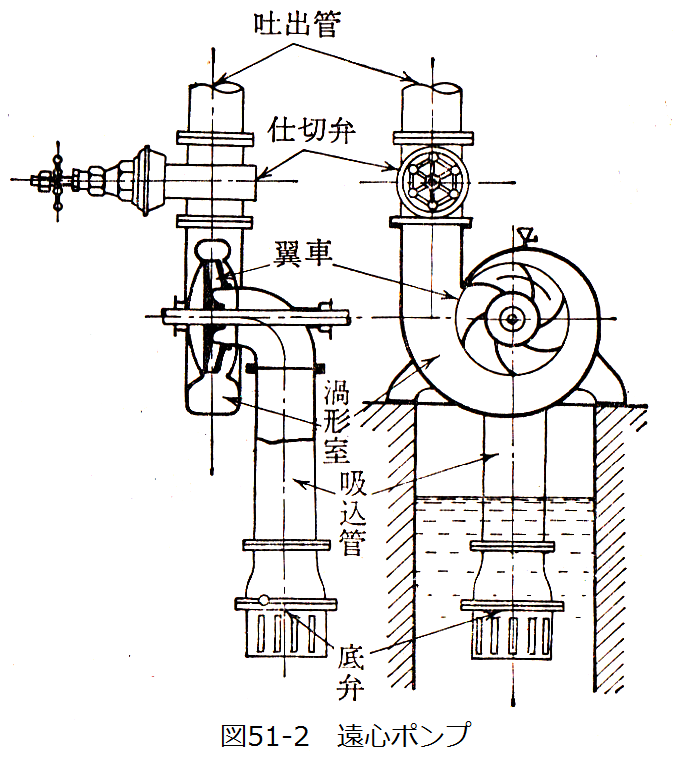
遠心ポンプの構造遠心ポンプは図51-2に示すように、翼車、うず形室、吸込み管、吐出管、底弁、仕切り弁より構成されます。ポ ンプの主要部分は翼車、うず形室です。水で満たされたうず形室内で翼車を回転すると遠心作用によって水は翼 車の外周より流出し、うず形室で集められ吐出管から押し出されます。このようなポンプを遠心ポンプと呼びます。
また、底弁は逆流防止、仕切り弁は揚水量の調整の役目をはたします。
翼車が流体に与える動力
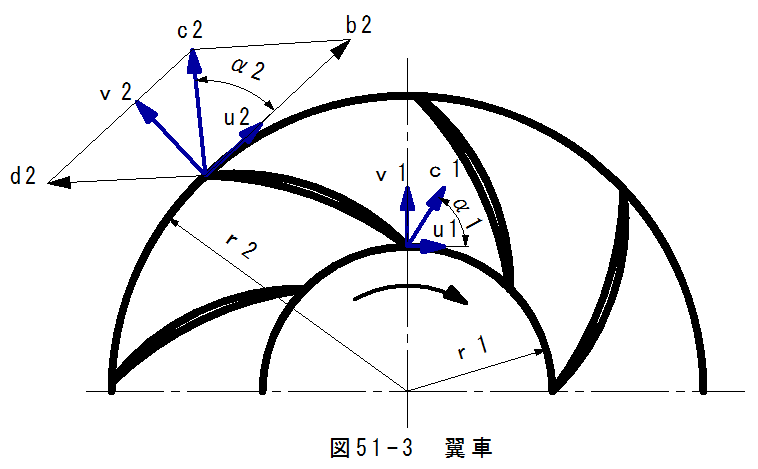
図51-3に示す翼車において2点は回転によりb2の周方向速度となります。流体は翼車の羽の形状にそって流れる ためd2の速度を持ちます。流体は合成速度はb2とｄ2の合成となり、ｃ2の速度を持ちます、ｃ2の円周方向分速度 をu2とした場合、翼車のモーメントMは
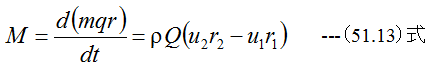
となります。翼車の回転角速度をωとした場合の翼車が流体に与える動力Pは
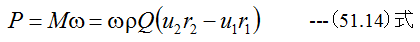
となります。
例題51-1外形276mm、内径139mmの翼車を有する遠心ポンプがあり、毎分1450rpmで回転するとき、翼車外形における周 方向分速度が14m/s、翼車内形における周方向分速度が0m/sで流量が2.6ｍ3/minとしたときの動力を求めよ。
解答
角速度ωは
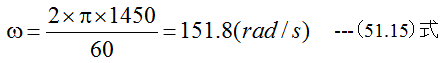
動力Pは（51.14）式から
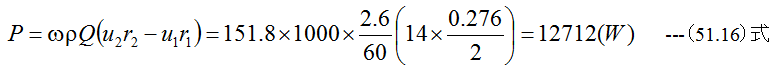
となります。
例題51-1の解説例題51-1は流量Qと翼車外形における周方向分速度u2が与えられているため、 （51.14）式で簡単に動力Pが計算で きます。しかし、流量Qと周方向分速度u2をどのように求めるか？明確ではありません。
角速度ωが与えられており、翼車の周方向速度ｂ2は容易に計算できます。角度α2とb2とu2の関係は
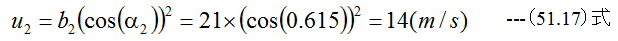
となり、角度α2＝0.615rad（35.3°）であることがわかります。また流体の半径方向分速度ｖ2は
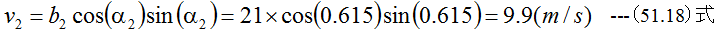
となります。翼車のｒ2における厚さをｚ2とした場合の流量Qは（51.10）式から
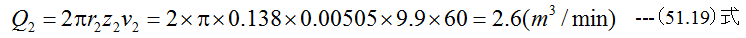
となり、翼車のｒ2における厚さｚ2＝5.05mmとなることがわかります。翼車の内周では半径rと半径方向流速vが 小さくなるため翼車の厚さｚは大きくする必要があります。
これらの特性は翼車の羽の形状、大きさ、厚さに大きく依存します。
なお、ポンプによって得られた動力（単位時間あたりの仕事量Pは
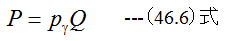
の関係があります。従って圧力増加pγは
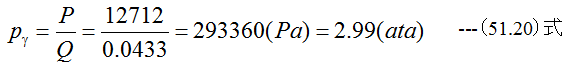
となります。
軸流ポンプの構造
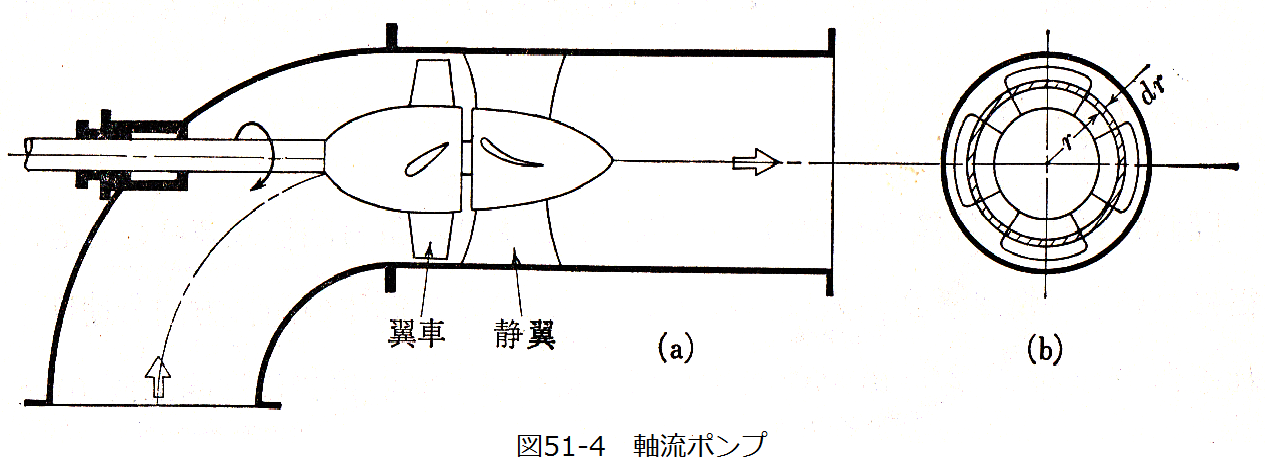
図51-4に軸流ポンプを示します。プロペラ形の翼車の回転により、吸込まれた流体は軸心にそって送り出 されます。軸流ポンプは一般に大流量、低揚程を必要とする場合に適します。
軸流ポンプの理論
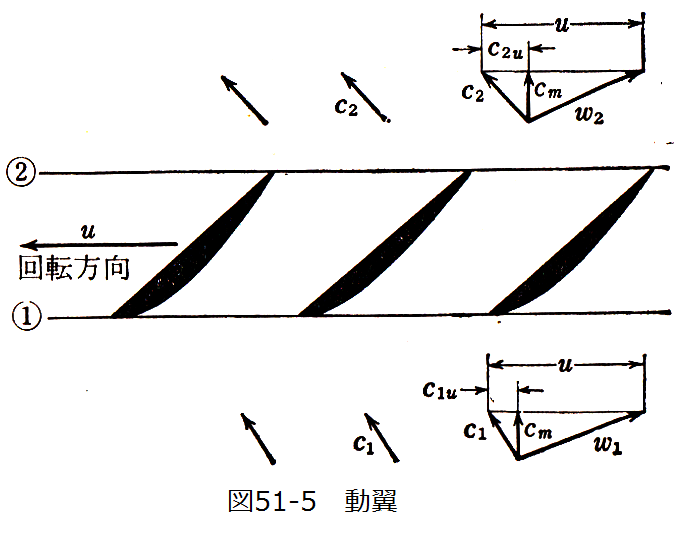
動翼を軸心より半径ｒの位置の円筒面で切って、これを平面に展開すると図51-5に示すようになります。
翼車の入口1で絶対速度c1で吸込まれた流体は、翼車出口で絶対速度c2で押し出されます。
また、動翼の円周方向速度をu、入口1での円周方向分速度をc1u、入口2での円周方向分速度をc2uとします。
図51-4の(b)に示すように半径r+drとrの間の流体について考えます。この部分で翼車が回転方向に流体に与える 力をdF、この断面を通る流量をdQとして、回転方向に運動量の法則を適用すると
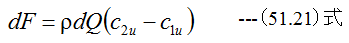
従ってこの部分の動力dPは
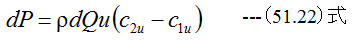
となります。 （46.6）式は
に変形できます。 （51.22）式と（51.23）式から
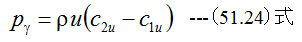
となります。
例題51-2外形980mmの軸流ポンプがあり、毎分回転数300rpmのとき、外形において翼車翼列の入口の流体分速度が 0m/s、出口の流体分速度が2.08m/sとすれば、このポンプの圧力増加は何Paか？
解答
（51.24）式から
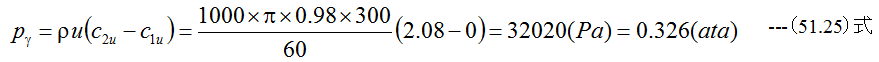
となります。例題51-2も例題51-1同様に流体分速度が与えられているため、簡単に計算できます。流体分速度 が不明の場合は翼車の羽の形状から計算する必要が生じます。
５２章：円管の流れとレイノルズ数に行く。