レイノルズ数の定義
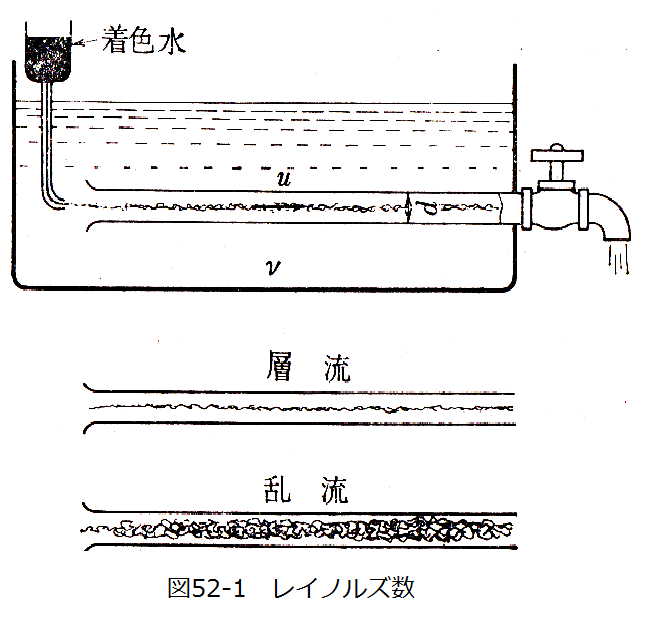
図52-1に示すように水が流れるガラス管内に軸心にそって色素の溶液を合流すると、流速が小さい間は、この溶液は形をくず さず、そのまま線状に流れるのが見られるが、流速が大きくなると、水と色素の溶液は合流直後から入り乱れて混流してしまう。
前者のように層状の流れを層流と呼び、後者のように入り乱れた流れを乱流と呼びます。
動粘性係数をν、管内の平均流速をu、管の内径をdとするとレイノルズ数は下記式で定義されます。
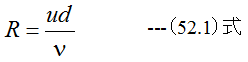
レイノルズ数Rは無次元の定数であり多くの実験により、レイノルズ数Rが同一ならば流れが力学的に相似となることが確認されています。
なお熱力学において、Rはガス定数として用いられていますが、流体ではレイノルズ数としてもちいられます。混同に注意する必要があります。
実験的にレイノルズ数Rが2310以下で層流、以上で乱流となることが確認されています。
例題52-120℃の水を内径20mmの円管に通した場合、どのような流速で層流から乱流に変化するか？
解答
４３章：粘性係数と動粘性係数、水の粘性係数図43-2から
水の比質量ρは1ｇ/cm3です。従って20℃の動粘性係数は
ν＝μ/ρ＝0.01/1＝0.01cm2/sとなります。
標準単位に変換すると
0.01cm2/s＝0.000001m2/sとなります。
従って（52.1）式から
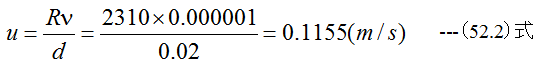
となります。層流から乱流に変化する流速は、低速であり多くの条件では乱流となることがわかります。乱流のような複雑な流れは理論的に解 を求めることが困難なため、流れの解析は実験的な要素が多くなります。
滑らかな円管
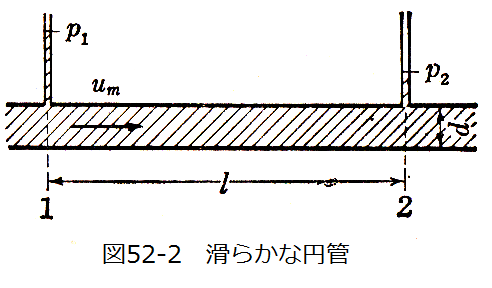
管の内壁が滑らかで、真直な水平円管の中を液体が定常的に流れている。上流1の圧力をp1、下流2の圧力をp2として圧力損失p1-p2の式を求めます。
1-2間の長さをｌ、管の直径をd、流体の管壁における摩擦応力をτとして、1-2間の流れについて運動量の法則を適用すれば
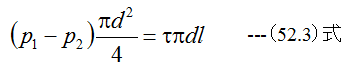
摩擦応力τは動圧に比例するとして
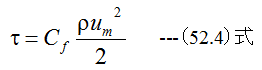
（52.4）式において、Cfは摩擦応力係数、ρは比質量、umは平均流速です。 （52.3）式に（52.4）式を代入して整理すると
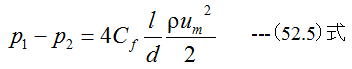
となります。ここで
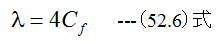
とするならば
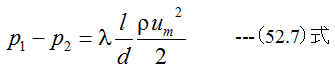
となります。（52.7）式のλは無次元の定数であり、管摩擦係数または圧力降下係数と呼ばれます。
層流の管摩擦係数λ
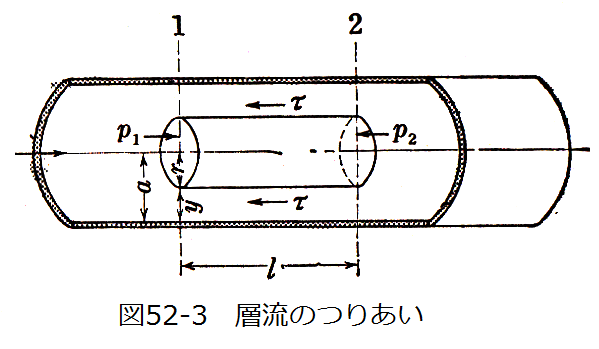
図52-3に示す層流において運動量の法則から
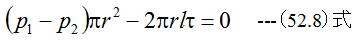
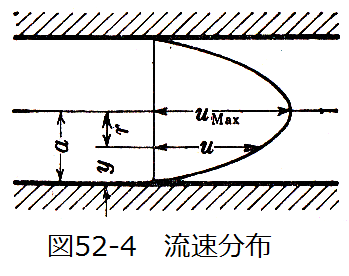
図52-4に示すように、半径ｒにおける流速をuとする。管壁からの距離をｙとしたとき
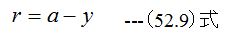
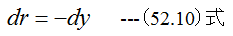
ゆえに粘性係数をμとすれば
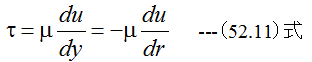
（52.8）式に（52.11）式を代入して整理すると
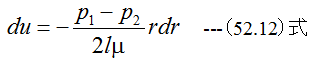
r=aでu=0の条件で（52.12）式を積分すると
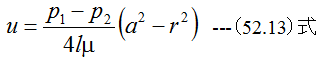
となります。つぎに流量Qは
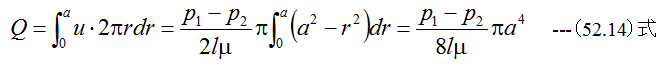
となります。平均流速umは
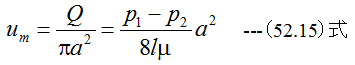
となります。また
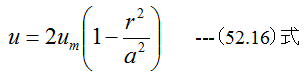
の関係式も得られます。
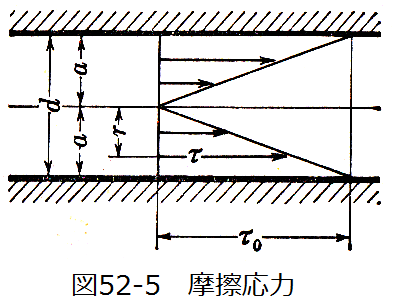
図52-5に示すように任意の半径ｒにおける摩擦応力τは（52.11）式と（52.16）式から
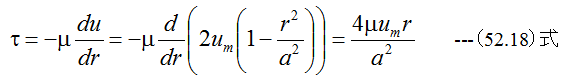
となります。 （52.1）式より管壁r=aにおいて摩擦応力τは最大となります。
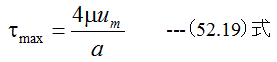
管摩擦係数λは（52.6）式と（52.4）式から
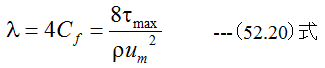
（52.20）式に（52.19）式を代入して整理すれば
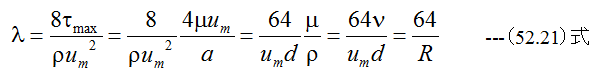
となります。 （52.21）式は理論的に導かれた式ですが、実験値と良く一致することが確認されています。
乱流の管摩擦係数λ乱流の場合は、理論的に求めることはできず実験式を求めることになります。
図52-6に滑らかな円管の管摩擦係数λ実験値グラフを示します。
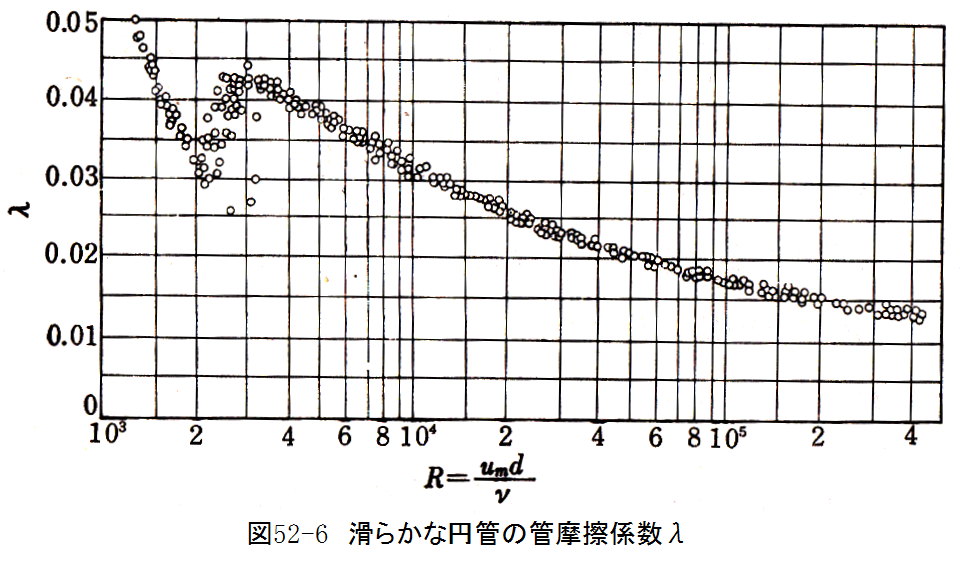
レイノルズ数R＝3000以上で良く一致する実験式は下記のプラントルの式です。
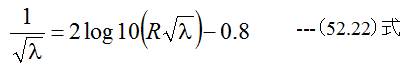
管摩擦係数λが両辺にあるため計算しにくいのですが、良く一致する実験式として提唱されています。
滑らかな円管の管摩擦係数λのEXCEL数表図52-6の滑らかな円管の管摩擦係数λ実験値グラフから正確な値を読み取るのは厄介ですのでEXCEL数表に まとめると扱いやすくなります。
レイノルズ数Rが2310以下では（52.21）式を適用
レイノルズ数Rが3000以上では（52.22）式を適用
レイノルズ数Rが2310以上3000以下は直線補間としました。
加熱蒸気表のワークブック「管摩擦係数-1.xls」のダウンロード
下記のワークブック「管摩擦係数-1.xls 」をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「管摩擦係数-1.xls 」をダウンロードする。ワークブック「管摩擦係数-1.xls 」説明
シート「管摩擦係数表 (滑らかな円管)」が数表です。
黄色のセル「A5セル」に値を入力すると補間計算できます。
滑らかな円管の管摩擦係数λのEXCEL数表のグラフを図52-7に示します。
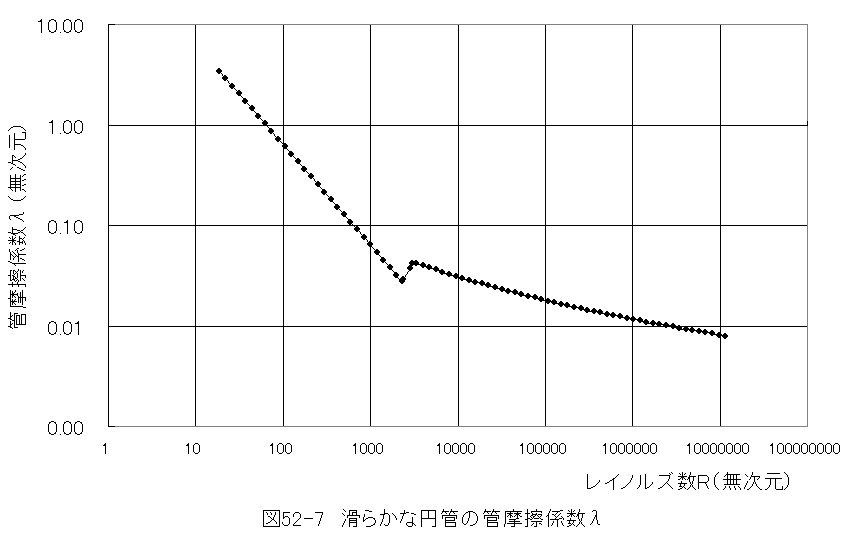
例題52-2内径70mmの真直な円管に風速30m/sの空気を通したところ円管の長さ1m間の静圧差が水柱16mmとなった。この 円管の管摩擦係数λを求めよ。ただし、空気は1.033ata、20℃、相対湿度0.5で比質量ρ＝1.2kg/m3とする。
解答
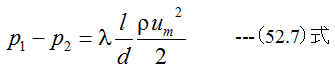
（52.7）式を変形すると
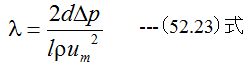
ここで
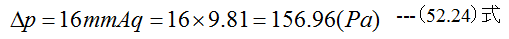
したがって
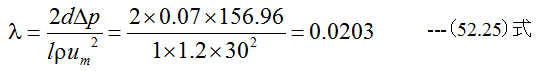
となります。
例題52-3内径18cm、長さ1500mの滑らかな理想円管を通して、20℃の水を流量7m3／minで送り出すにはどれ だけの圧力を必要とするか？また必要動力はいくらか？
解答
４３章：粘性係数と動粘性係数、水の粘性係数図43-2から
水の比質量ρは1ｇ/cm3(1000kg/m3）です。従って20℃の動粘性係数は
ν＝μ/ρ＝0.01/1＝0.01cm2/sとなります。
標準単位に変換すると 0.01cm2/s＝0.000001m2/sとなります。
平均流速umは
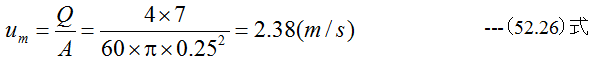
レイノルズ数Rは（52.1）式から
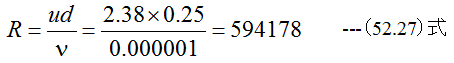
滑らかな円管の管摩擦係数λのEXCEL数表からλ＝0.01276となります。圧力差は（52.7）式から
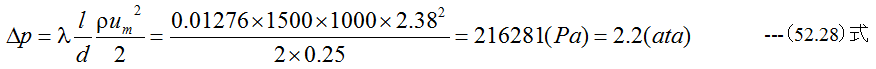
となります。また必要動力Pは
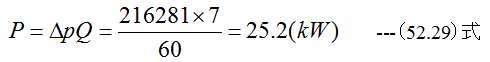
となります。この例題においては滑らかな理想円管としましたが、実際の管の内面には凹凸 があり圧力損失が増大するため、必要動力も増大します。
例題52-4例題52-3と同条件で流量を1〜7m3／minに変化させた場合の圧力損失と必要動力を求めよ。
解答
計算式は例題52-3と同一となります。
計算結果を表52-1に示します。
表52-1 流量と圧力損失と必要動力の関係
| 流量Q | 流速um | レイノルズ数R | 管摩擦係数λ | 圧力損失Δp | 必要動力P |
| m3/min | m/s | 無次元 | 無次元 | kPa | ｋW |
| 1 | 0.340 | 84883 | 0.01864 | 6.4 | 0.11 |
| 2 | 0.679 | 169765 | 0.01617 | 22.4 | 0.75 |
| 3 | 1.019 | 254648 | 0.01493 | 46.5 | 2.32 |
| 4 | 1.358 | 339531 | 0.01414 | 78.3 | 5.22 |
| 5 | 1.698 | 424413 | 0.01356 | 117.3 | 9.77 |
| 6 | 2.037 | 509296 | 0.01312 | 163.3 | 16.33 |
| 7 | 2.377 | 594178 | 0.01276 | 216.3 | 25.23 |
表52-1から流速を大きくすると、急激に圧力損失と必要動力が増大することがわかります。パイプ ラインの運用に関して流速をできるだけ小さくすることが、省エネ上重要となります。
５３章：粗い円管の管摩擦係数λに行く。