水力平均深さm
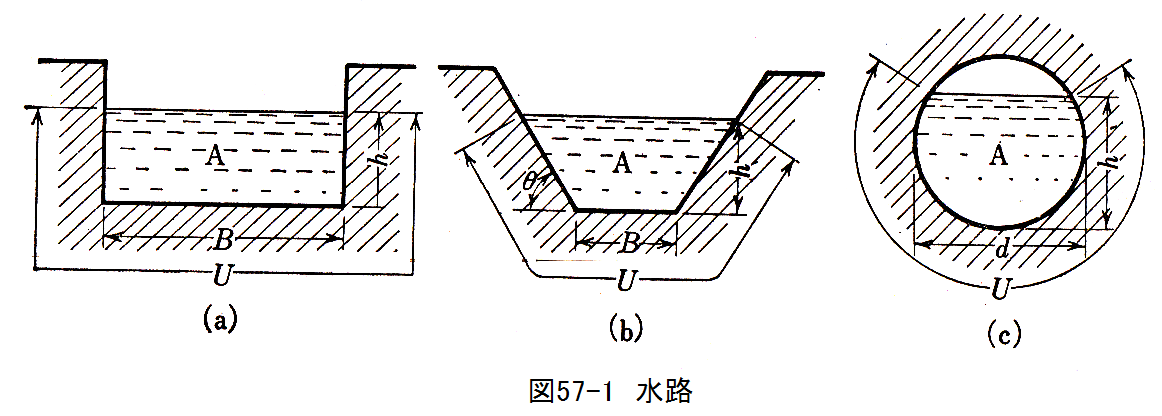
水路においては、水力平均深さmが使用されます。流れの断面積をA、大気を除く水路壁面の長 さをUとしたとき、水力平均深さmは
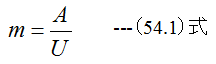
と定義されます。
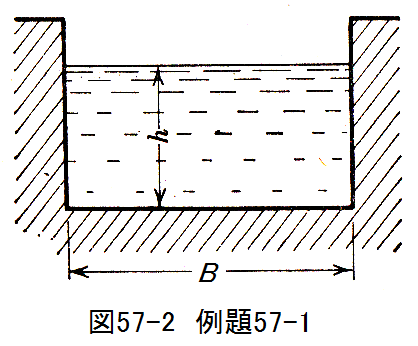
例題57-1図57-2に示す矩形の水路において、最も摩擦抵抗が少ないBとhの比を求めよ。
解答
大気を除く水路壁面の長さUは
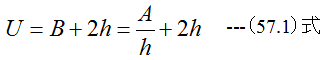
Uが最小となる条件は
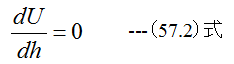
従って
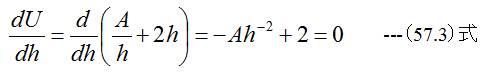
ゆえに
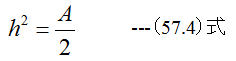
（57.4）式にA=Bhを代入して整理すると
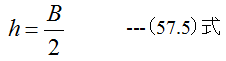
となります。
流速が一定の水路
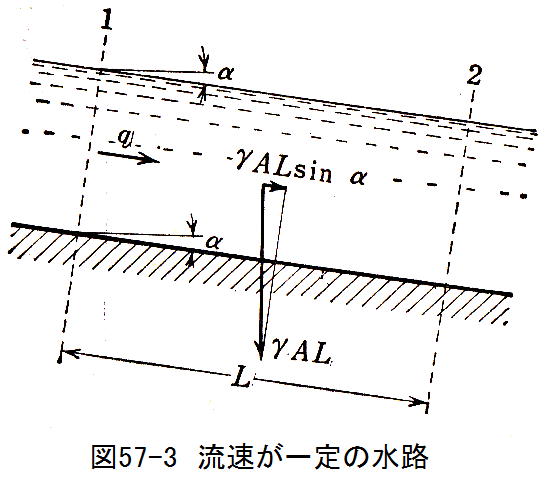
図57-3に示すように、傾き角α、流れの断面積Aの水路内を液体が流速q一定で流れているとする。 1-2間の流体が流れの方向に引かれる力Fは
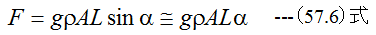
となる。流れを止めようとする力Fは、せん断応力をτ0とすると
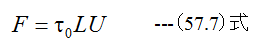
両者は等しく
せん断応力をτ0は動圧に比例するとして
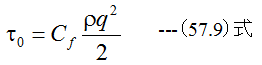
（57.8）式に（57.9）式を代入して整理すると
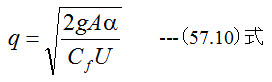
となります。 （57.10）式にm=A/U代入して整理すると
となります。 （57.11）式は理論的に予想される式ですが、Manningの実験式とは一致しません。水路の 流れは複雑であり、 （57.9）式の条件が厳密には成立しないのかもしれません。
Manningの実験式は
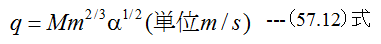
となります。Mは壁面の種類と状態で異なる定数となります。
M定数表を表57-1に示します。
表57-1 M定数表
| 壁面の種類 | 状態 | M値 |
| 木材 | かんなをかけたもの | 90 |
| 木材 | かんなをかけないもの | 80 |
| 木材 | ふるいもの | 65〜70 |
| コンクリート | 上塗りを行ない滑らかなもの | 90〜95 |
| コンクリート | 砂利露出のもの | 50 |
| 金属 | 滑らかなもの | 90〜95 |
| 金属 | リベット頭の出ているもの | 55〜75 |
| 堀さく開渠 | でい砂 | 60 |
| 堀さく開渠 | 砂をまじえた砂れき | 50 |
| 堀さく開渠 | 砂れき | 40 |
| 自然の河川 | 侵食、輸送のないもの | 40 |
| 自然の河川 | 侵食、輸送のあるもの | 35 |
| 自然の河川 | 同上で雑草のはえているもの | 30 |
例題57-2幅b=6mの矩形断面のコンクリート製（上塗りして滑らか）があり、傾斜が0.001の場合、水深hと流速の関 係をグラフにせよ。
解答
水力平均深さmは
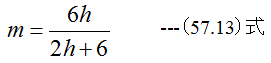
M=90とすると流速qは
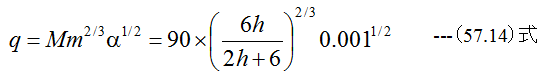
となります。
計算結果を図57-4に示します。
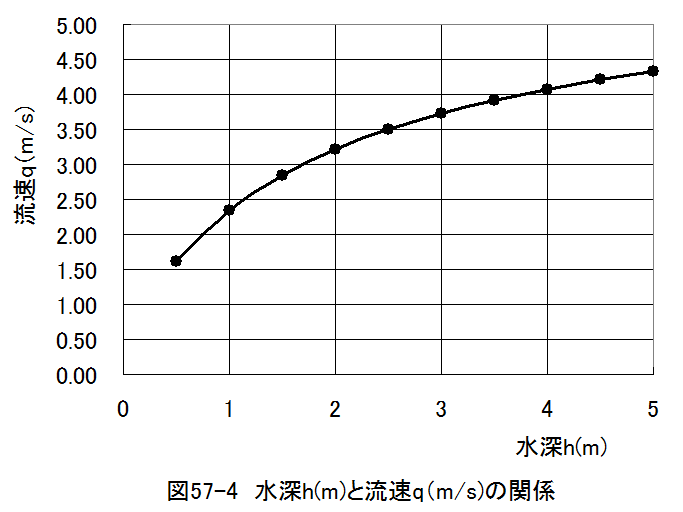
図57-4から流速qは1.62m/s（5.8km/h）から4.33m/s（15.6km/h)の間で変化することがわかります。（自然の 河川と比較すると早くなります。）
５８章：オリフィスに行く。