管の途中に丸い穴の開いた仕切り板を設けた場合、この仕切り板をオリフィスといいます。流体が ここを通るとオリフィスの前後で圧力差が生じます。
具体的な応用例としてはエアーベアリングのオリフィスがあります。
オリフィスの実験式
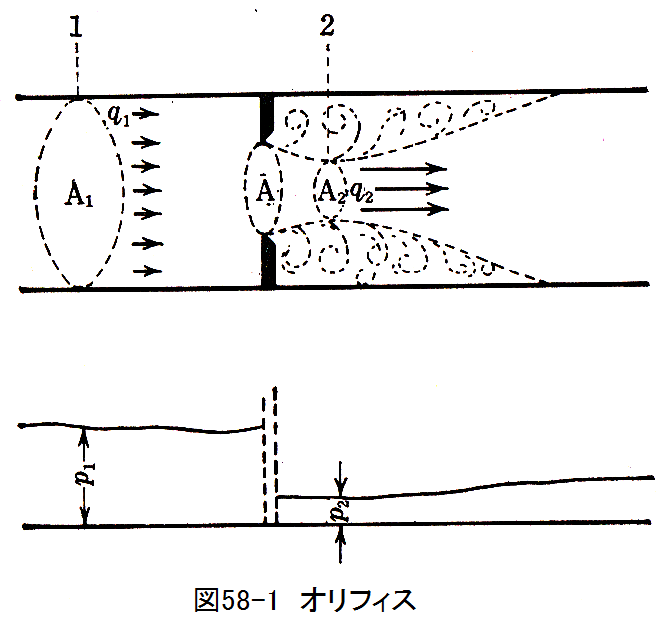
図58-1に示すように管（断面積A1）内の流れはオリフィス(断面積A)を出たところで、その主流は最小断面 （断面積A2)に絞られた後、漸次膨張して管一杯に流れます。
A1、A2における平均流速をq1、q2とすればベルヌーイの式より
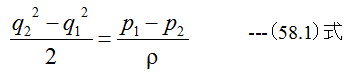
また連続条件から
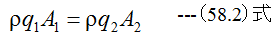
（58.1）式に（58.2）式を代入して整理すれば
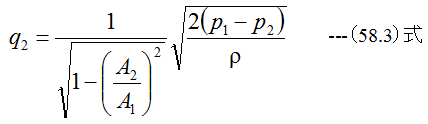
となります。流量Qは
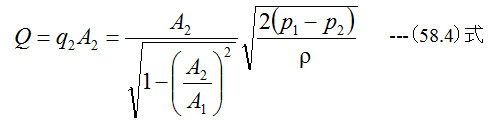
ここで
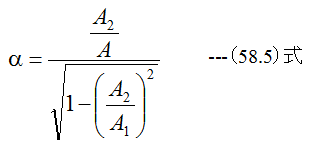
とするならば
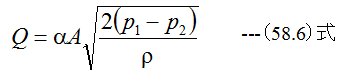
となります。 （58.5）式がオリフィスの実験式であり、定数αを流量係数といいます。流 量係数αは無次元であり、実験的に求めます。
流量係数α
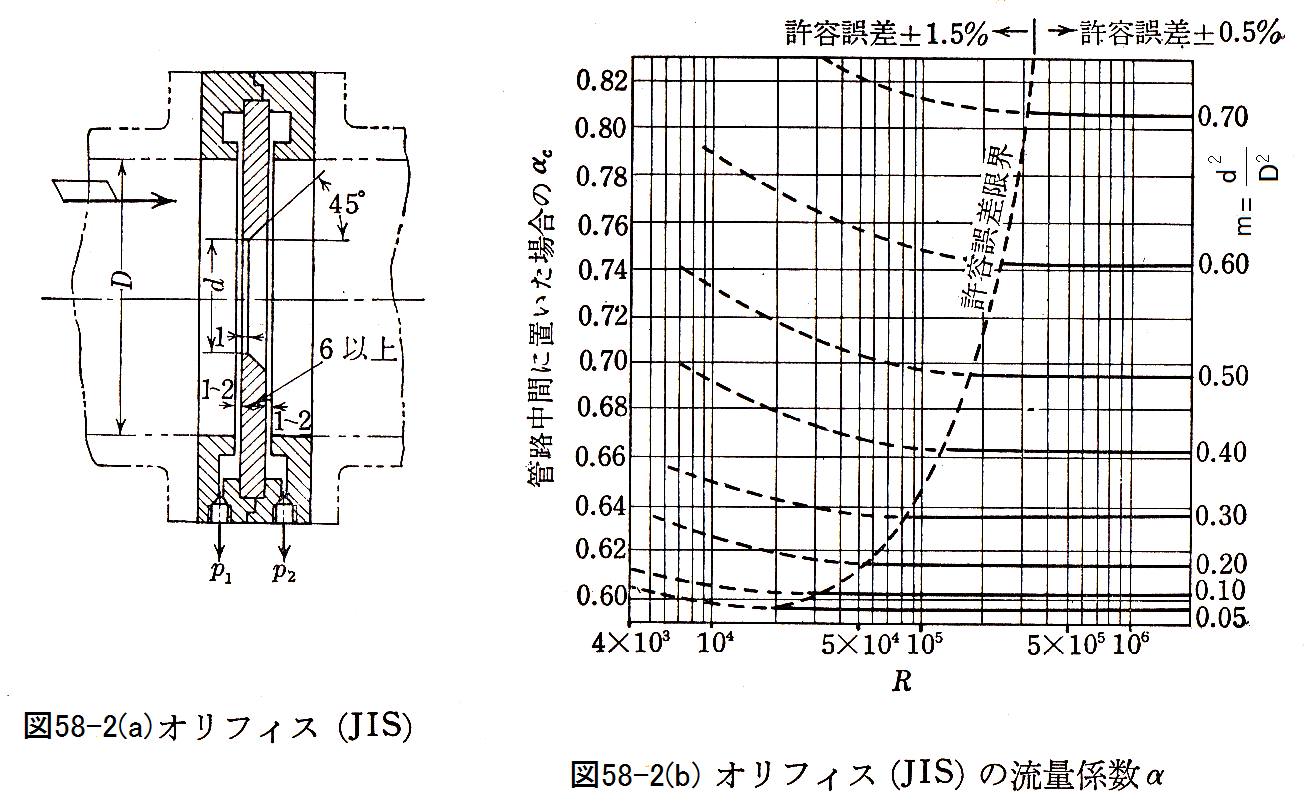
図58-2(a)にJISオリフィスの形状と圧力p1、ｐ2の測定条件を示します。図58-2(b)は各種条件における管路中 間においた場合の流量係数α（単位無次元）の値を示します。ここでレイノルズ数Rは
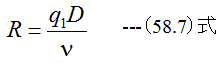
で定義されます。また面積比mは
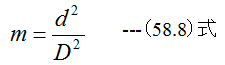
で定義されます。図58-2(b)からわかるようにレイノルズ数Rが一定値以上において、流量係数αは一定値となり ことがわかります。
オリフィスを管路の入口、途中、出口につけた場合オリフィスを管路の入口、途中、出口につけた場合の流量係数αe、αc、αaとしたグラフを図58-3に示します。
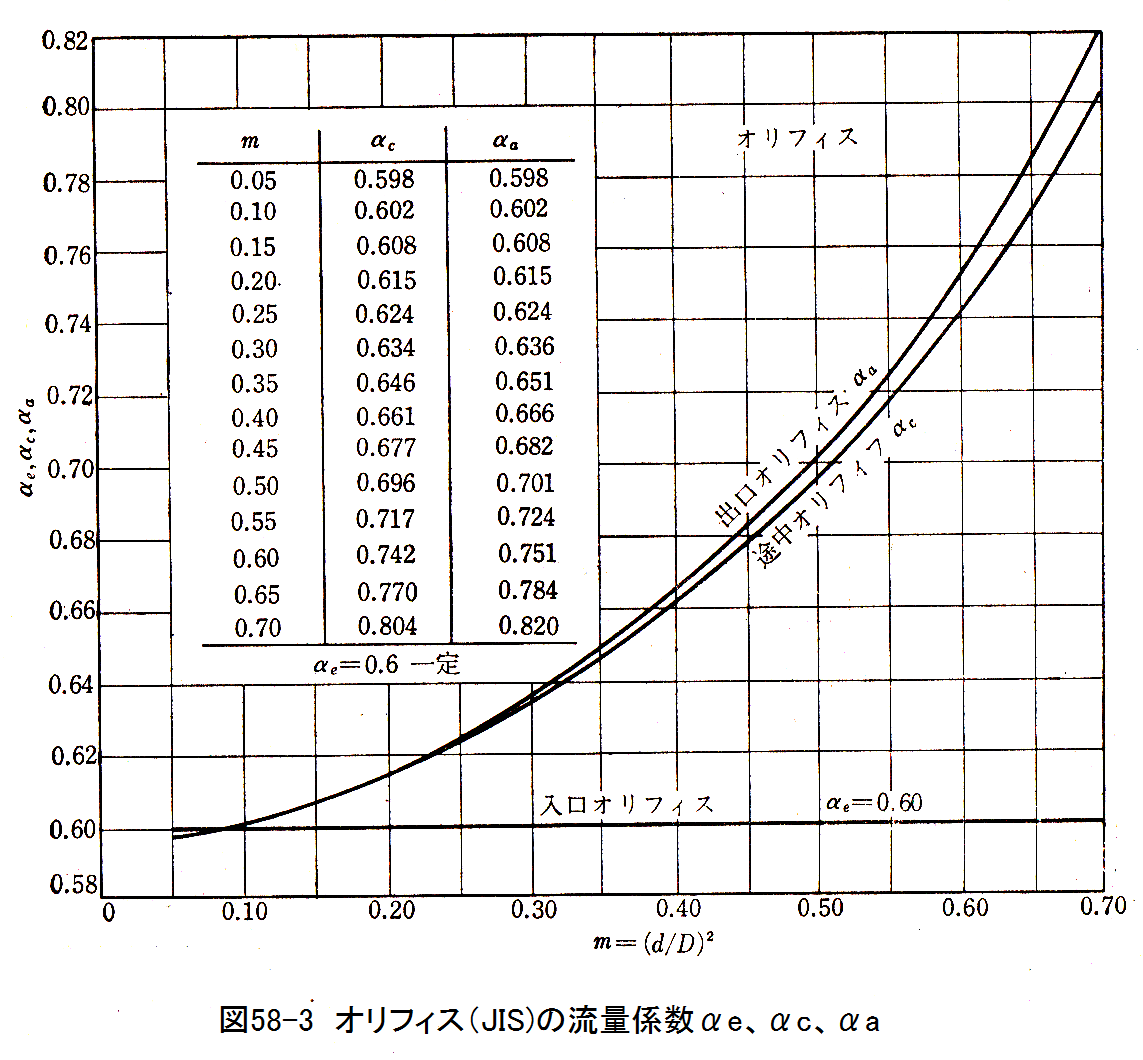
図58-3はレイノルズ数Rが十分大きいときの流量係数です。オリフィスを管路の入口につけるとD=∞ となり、m=0となります。
従って、流量係数αe＝0.6で一定となります。m=0.05においてαc=αa=0.598となりますが
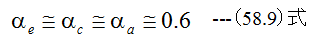
としても問題ないと思います。
気体の実験式気体の場合は液体の流量係数αに補正係数εをかけて補正します。気体の実験式は
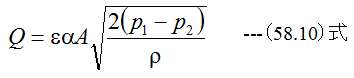
となります。補正係数εの値を図58-4に示します。
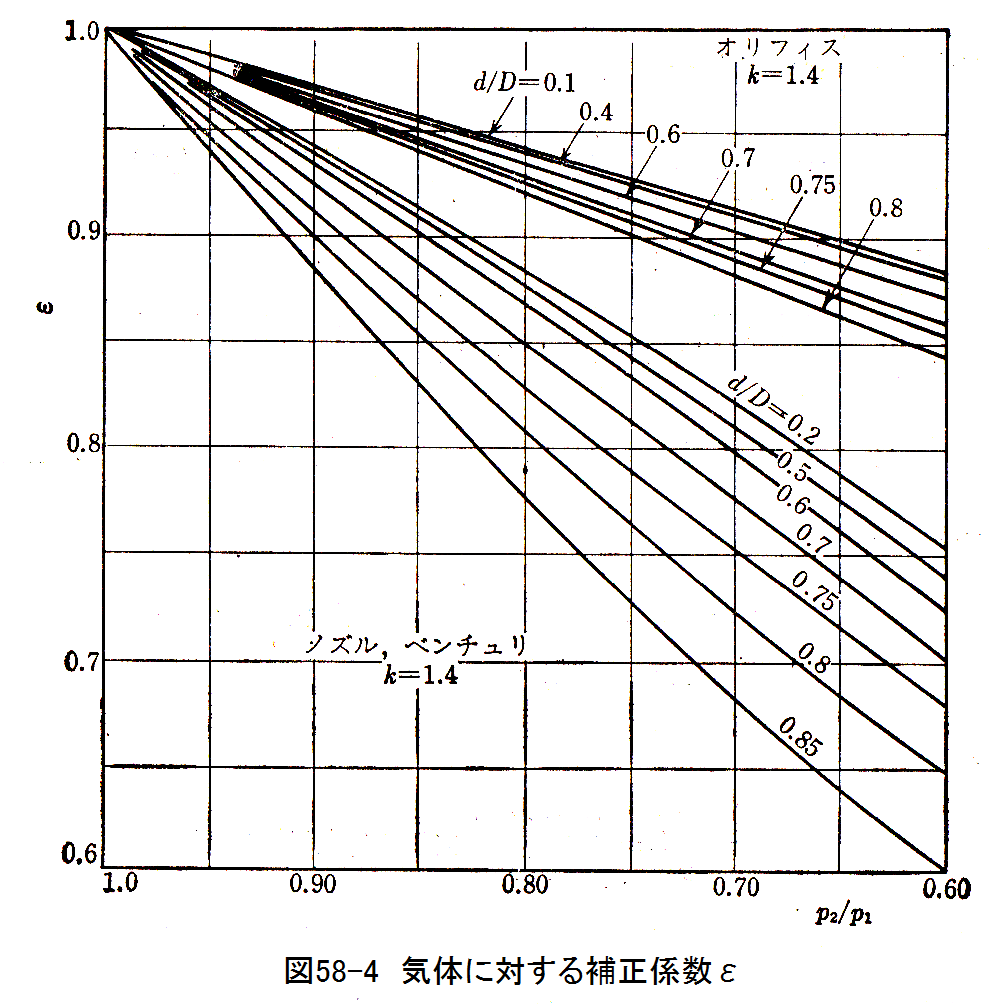
図58-4は、オリフィスとノズル・ベンチュリの補正係数εであり、圧力比p2/p1と直径比d/Dで変化します。
例題58-1内径20cmの円管の途中に孔径11cmのJIS規格のオリフィスを取付けて、この中を通る空気量を計測します。オリ フィス前後の圧力差が1216Paになったとすれば空気の流量は何m3/sになるか？
オリフィス直前の圧力は101990Pa、温度は20℃とする。
解答
面積比は
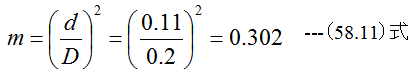
圧力比は
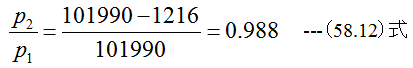
流量係数αは図58-3から
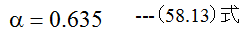
補正係数εは図58-4から
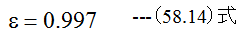
空気の比質量ρは圧力ｐの単位がPaの場合
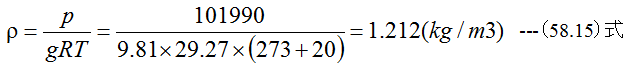
従って流量Qは
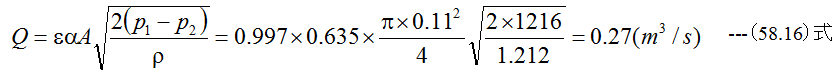
管内の平均流速q1は
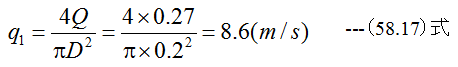
図43-3のグラフから20℃の空気の粘性係数は約0.00018ｇ/cm・sです。これは 0.00018ｇ/cm・s ＝ 0.000018 Pa・sに相当します。
動粘性係数ν＝μ/ρ＝ 0.000018 /1.212＝0.0000149（ｍ2/s)となります。
レイノルズ数Rは
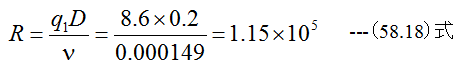
図58-2(b)においてm=0.3ではR＝85000以上で流量係数αは一定となります。これ は上記の流量計算が成立することを意味します。
５９章：ノズルとベンチュリ管に行く。