流体中を物体進行する場合、または流れの中の物体が静止している場合、物体が流体から受 ける力を流体の抵抗または抗力といいます。
球体の抗力実験式
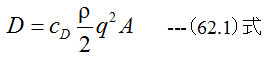
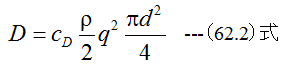
（62.1）式において、cDは無次元の係数で抗力係数といいます。抗力係数は実験的に求められます。ρ は比質量、qは流速、Aは断面積です。球の直径をdとすると(62.2)式となります。
球の抗力係数の実験データ
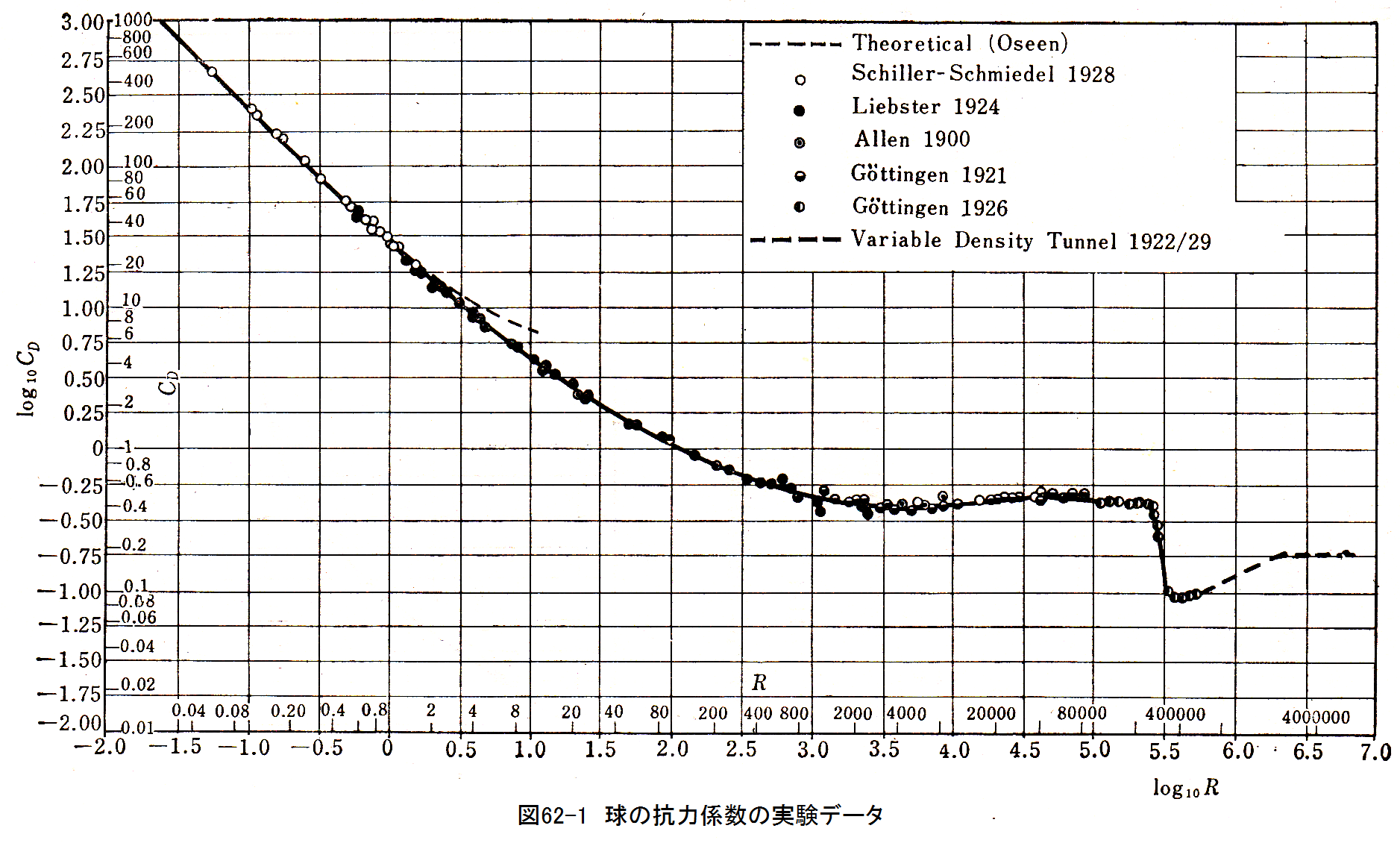
図62-1において球の抗力係数は
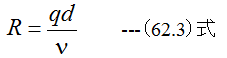
で与えられるレイノルズ数Rの関数となっています。また
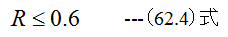
の領域においては
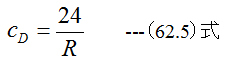
（62.5）式の関係式が成立します。
臨界レイノルズ数図62-1において、レイノルズ数R＝300000付近で球の抗力係数が約0.44から0.18に急激に変 化します。これを臨界レイノルズ数といいます。
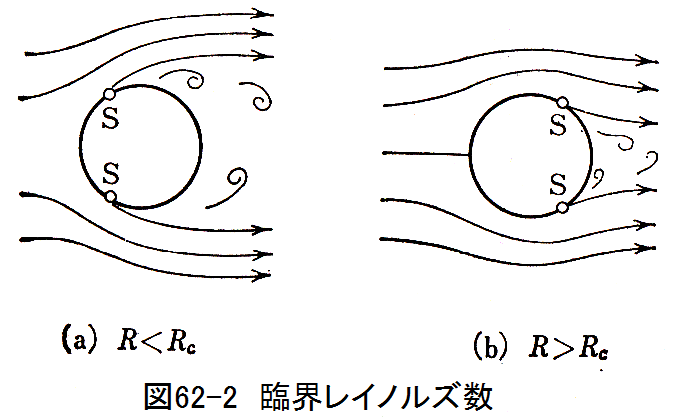
この現象は、図62-2(a)に示す剥離点Sが図62-2(ｂ)に示す位置に急激に変化するためと考えられています。
例題62-1直径1cmの球が空気中を30m/sの速度で飛ぶ場合の抗力を求めよ。ただし、空気の比質量は1.23kg/m3、動粘性 係数は0.15cm2/sとする。
解答
レイノルズ数は
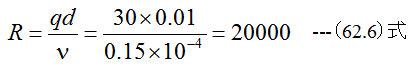
図62-1から抗力係数cDは
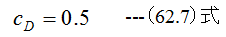
したがって抗力Dは
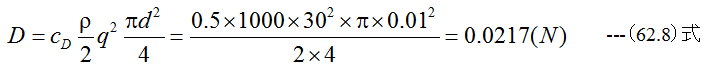
となります。
６３章：円柱とその他形状の抗力係数に行く。