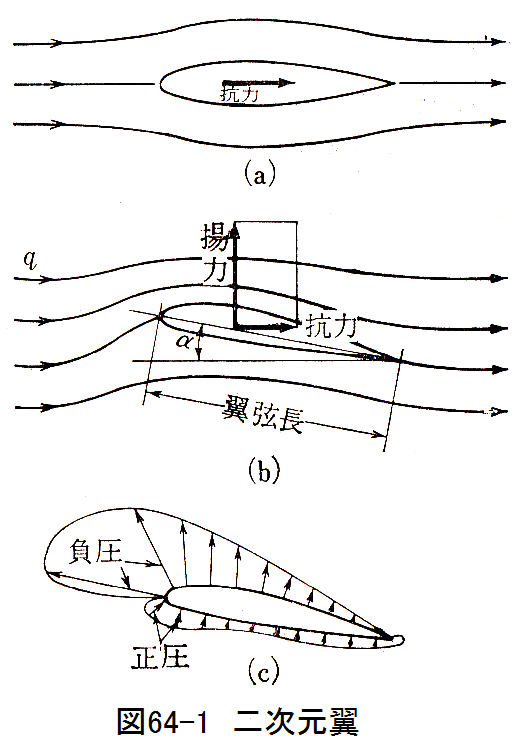
二次元翼図64-1に示すように、翼幅が無限大でどの断面でも流れの状態が同一な翼を二次元翼といいます。
図64-1(a)に示すように上下対称な翼を流れに平行に置いた場合、抗力のみが作用して揚力は生じません。
図64-1(b)に示すように、流れに対してある程度傾けて置くと上側の流速は早く、下側の流速は遅くなりま す。ベルヌーイの式より明らかなように上側の圧力は低く、下側の圧力は高くなります。この圧力差により揚 力が生じます。
図64-1(ｃ)は翼の表面の圧力分布の様子を示します。翼型は対称でなく上側のほうが丸まっています。これに よりさらに、上側の流速は早く下側の流速は遅くなります。
揚力をL、抗力をDとしたとき、実験式は
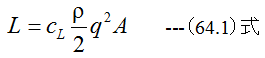
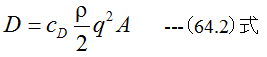
（64.1）式と（64.2）式において、cLは無次元の係数で揚力係数、cDは無次元の係数で抗力係数といいます。 ρは空気の比質量であり、qは流速、Aは翼の面積です。揚力係数と抗力係数は実験的に求められます。
揚力係数と抗力係数のグラフ例迎え角αを変数とした揚力係数と抗力係数のグラフ例を図64-2に示します。
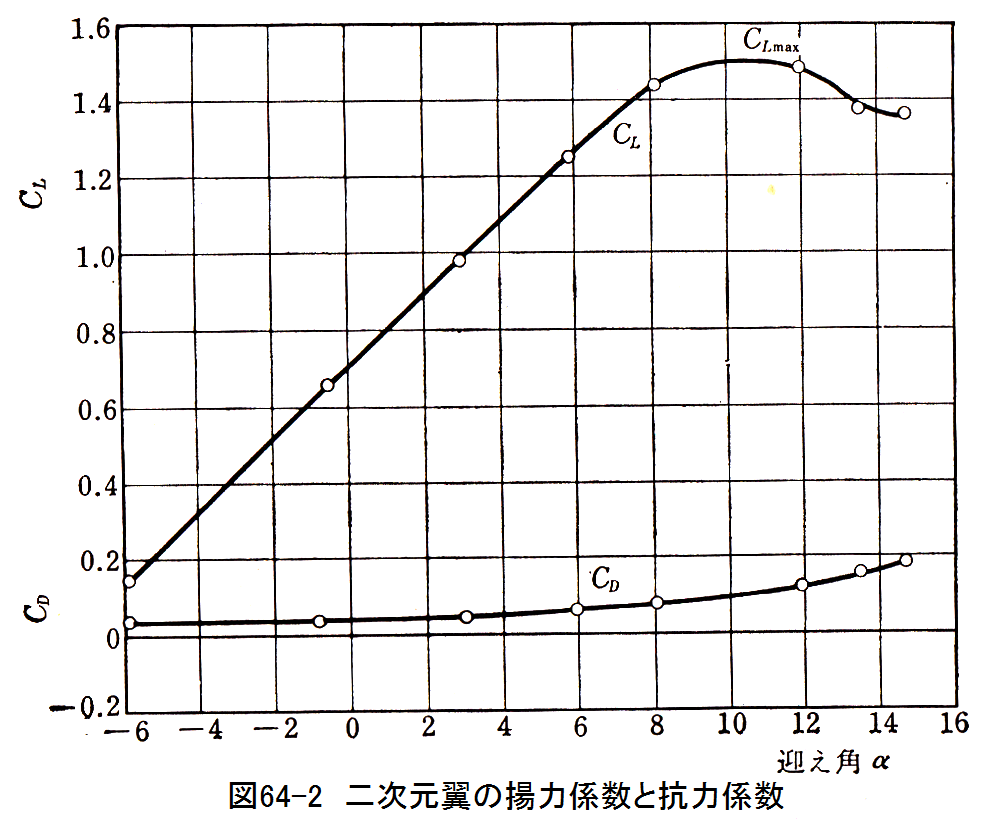
例題64-1図64-2に示す性能を有し、翼幅10m、翼弦長2mの翼が迎え角２°で10m/sの速度で飛ぶ場合、揚力、抗力はい くらか？ただし、空気の比質量は1.2kg/m3とする。また必要動力はいくらか？
解答
図64-2から迎え角２°における揚力係数と抗力係数は
従って、揚力Lと抗力Dは
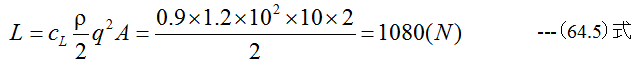
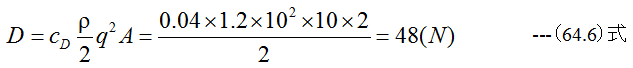
必要動力Pは
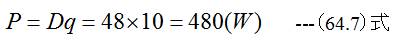
となります。
人力飛行は可能か？
毎年、人力飛行の大会があり可能なことは明らかです。例題64-1の条件において、揚力は1080（N)であり、 これは機体と操縦者の合計の質量が110kg以下であることが必要条件となります。
大きな問題は操縦者が480(W)以上の動力を継続できるか？この動力の値は、体重60ｋｇの操縦者が毎 秒0.815mの高さに駆け上るのに相当します。超人的なパワーと持続力が要求されます。
６５章：エアーベアリングパッドの最適化検討に行く。