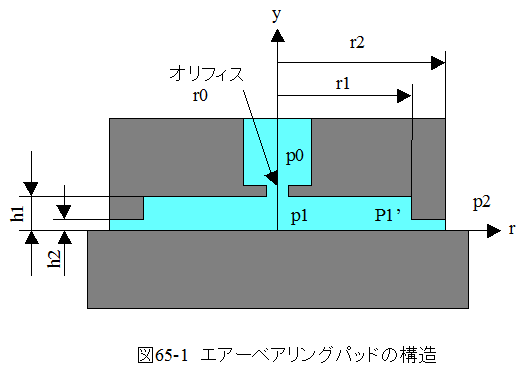
２平面間流れの基礎方程式図65-1に示すエアーベアリングパッドの構造において、供給圧力ｐ0はオリフィスを通過することによりｐ1に変化 し、隙間ｈ1とｈ2を通って大気(p2)に放出されます。
まず、ｒ＝0からr=r1、隙間h1における２平面間流れの基礎方程式を考えます。
２平面間流れの基礎方程式は
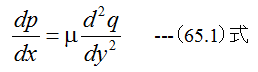
（65.1）式において、pは圧力、xは流れの方向の距離、μは粘性係数、qは流速、ｙは隙間方向距離です。ここで
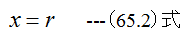
とするならば
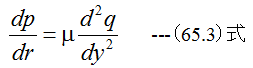
となります。（65.3）式の解は
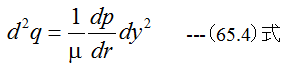
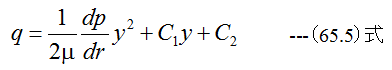
となります。ここで、ｙ=0とｙ=ｈにおいて、粘性流体の流速Uはゼロである条件を入れて積分定数C1とC2を求めます。
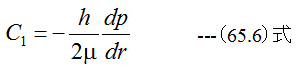
したがって
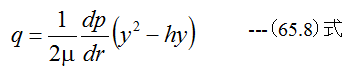
となります。半径ｒでの隙間hを通過する粘性流体の流量Qは
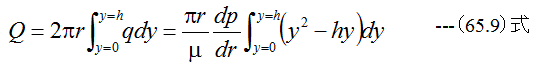
（65.9）式の積分を実行すると
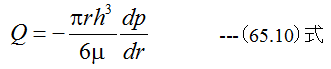
（65.10）式を変形して
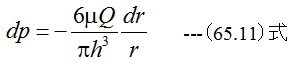
h=h1として、 （65.11）式をｒ0からｒ1まで積分すると
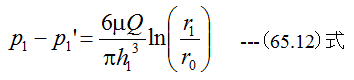
同様にh=h2として、 （65.11）式をｒ1からｒ2まで積分すると
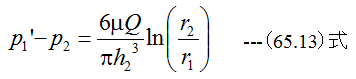
となります。
オリフィスによる圧力低下オリフィスの実験式は
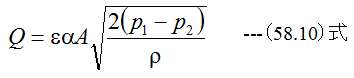
で与えられます。εは補正係数でありε＝0.9、αは流量係数でありα＝0.6、p1=p0 、ｐ2＝ｐ1とするならば（58.10）式は下記のようになります。
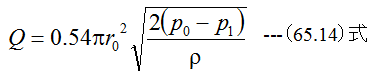
エアーベアリングパッドの特性式の誘導大気圧ｐ2＝0として、p1-p1’＝0とするならば
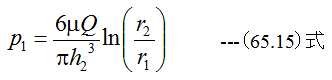
（65.15）式に（65.14）式を代入すると
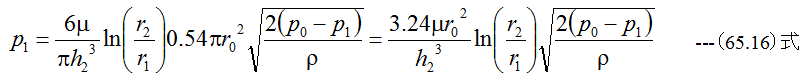
（65.16）式は以下のように変形できます。
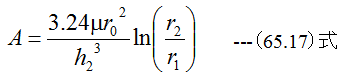
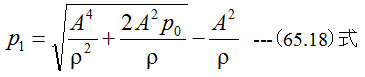
エアベアリングパッドの浮上力Fは
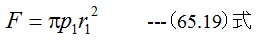
エアベアリングパッドの剛性Sは
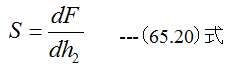
となります。
計算事例以下の条件で計算します。
比容積：ｖ=8.63E-01（m3/kg）
比質量：ρ = 1.16E+00 （ kg/m3)
粘性係数：μ = 1.80E-05 （ Pa・s)
動粘性係数：ν = 1.55E-05 （ｍ2/ｓ)
パッド内半径：r1 = 7.00E-02 （ m)
パッド外半径：r2 = 8.00E-02 （ m)
供給圧力：p0 = 5.00E+05 （ Pa)
また、オリフィス半径ｒ0は0.1mmと0.2mmで計算します。
圧力変化の計算結果を図65-2に示します。
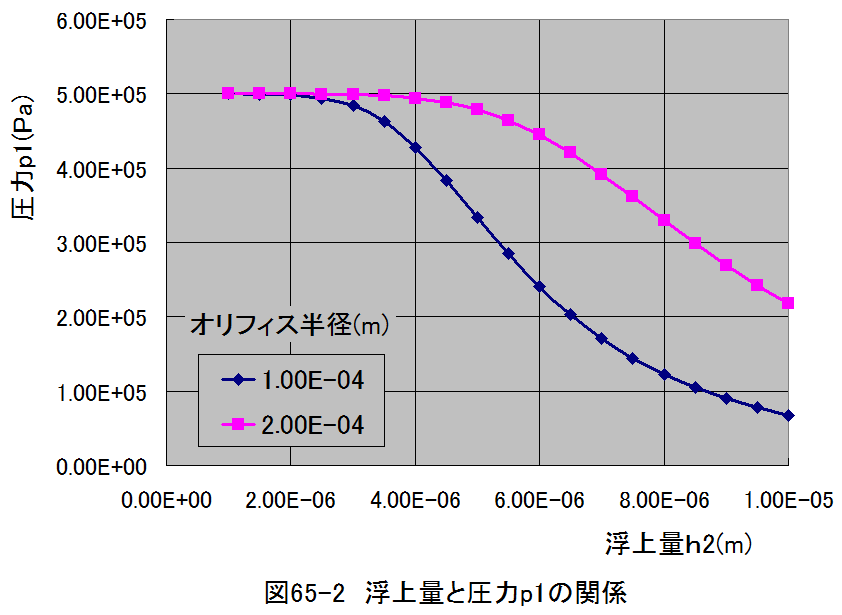
図65-2からオリフィス半径ｒ0＝0.1mmにおいては、浮上量が約5μmで急激に圧力p1が変化することがわかります。
剛性変化の計算結果を図65-3に示します。
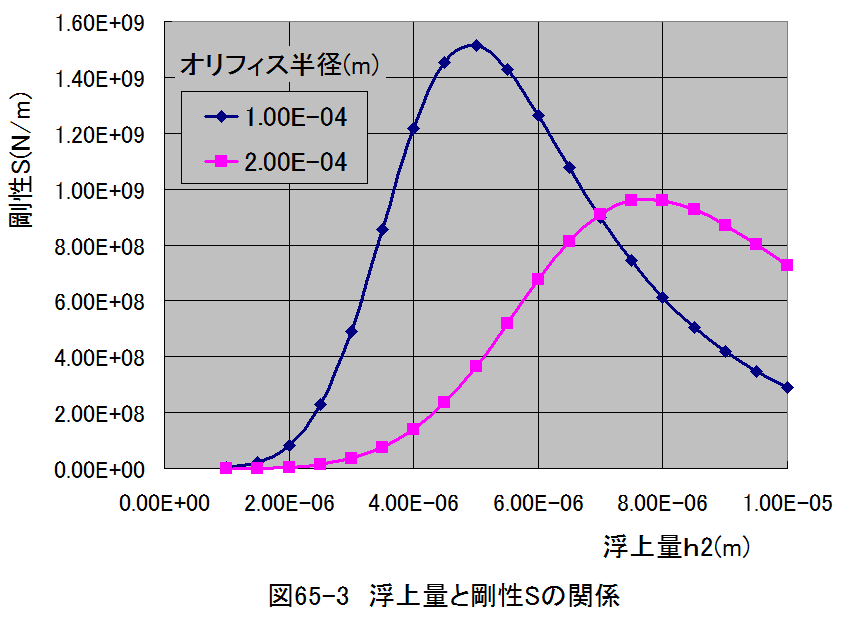
図65-3から、オリフィス半径ｒ0＝0.1mmにおいては、浮上量が約5μmで剛性Sが最大となることがわか ります。この時の剛性は1.5E+09(N/m)であり、浮上量1μmの変化に対して、浮上力が1500N変化します。
このことから、最適設計されたエアーベアリングは十分な剛性を持つことがわかります。
空気室での圧力損失（65.12）式と（65.13）式を加算すると
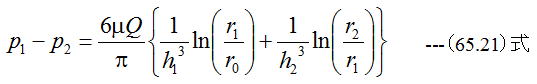
となります。したがって
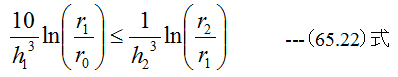
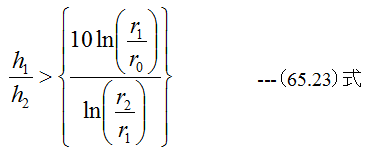
であれば、空気室での圧力損失は無視できると考えるべきです。
計算事例の値を代入すると
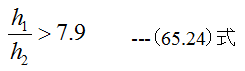
となります。従って浮上量が5μmの場合
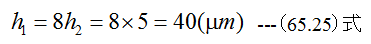
となります。
流体のまとめ流体は身近な物質ですが、流れは複雑であり多くの場合理論解を求めることが困難です。しかし、実用的には重 要であり多くの実験がおこなわれています。実験結果の一部は実験式と実験データの形で公開されていますので 、実験式と実験データを活用することが重要となります。
理論的には鮮やかさにかけますが、実験式と実験データの活用はさほど難しくはありません。
トップページに戻る。