直流発電機の原理と起電力直流発電機は構造が複雑で整流子が磨耗劣化するため、長期的な信頼性が要求される用途には適しませんが、直接直流電源が得られる特徴があります。
また、直流発電機を逆に使用すれば、直流モータとなります。
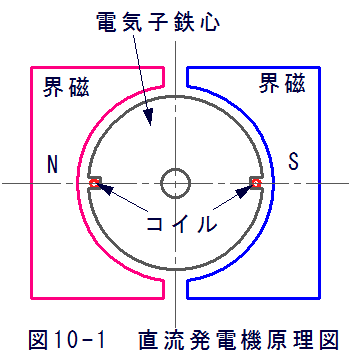
図10-1に直流発電機の原理図を示します。実際には界磁の磁極数もコイル数も多いのですが、ここではそれぞれ１ペアーとしています。
界磁磁極は永久磁石と電磁石の２種類があります。
電気子鉄心は界磁で発生する磁束の磁気抵抗を減らす作用があり、隙間が小さいほど磁気抵抗を減らすことができます。
磁束密度B〔T〕（〔Wb/m2〕）、胴体の長さl〔m〕、導体の移動方向が磁界と直角で速度がv〔m/s〕とすると、導 体が1s 間に移動する距離vtはv×1=v〔m〕、導体が磁束と交差する面積はlv〔m2〕、よって、1s 間の磁束の変化数 はBlv、よって起電力Eは
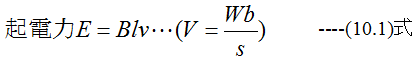
回転子の速度v〔m／s〕は直径D〔m〕、1秒間の回転数をn回〔rps〕とすると
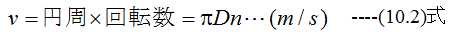
磁束密度（平均）B〔T〕は1極当たりの磁束をΦ〔Wb〕、極数をp、導体の長さをl〔m〕とすると、
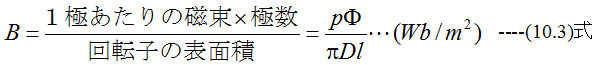
(10.1)式に(10.2)式と(10.2)式を代入すると
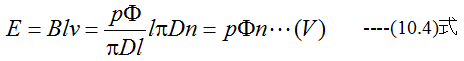
と比較的簡単な式となります。(10.4)式はコイル１個当たりの起電力となりますが、全コイルの 巻き数Zとコイルの並列結線数aで起電力は変化します。起電力の倍率mは
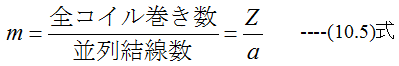
(10.4)式と(10.5)式から一般てきな直流発電機の起電力は
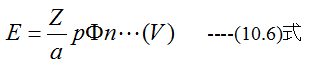
となります。
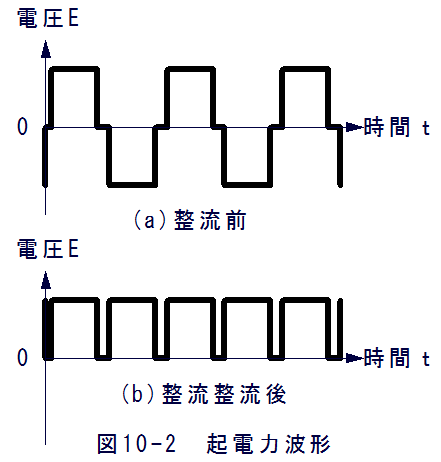
直流発電機の起電力波形直流発電機の磁束密度は界磁の切れ目で急激に変化し間は一定になるようにしてあります。このため、整流前の波形はSIN曲線とはならず、図10-2(a)に示すような矩形波となります。
これを整流器を通すと図10-2(b)に示すような波形となります。整流の切れ目での脈動は残りますがこの脈動はコンデンサで除去します。
直流発電機の構造
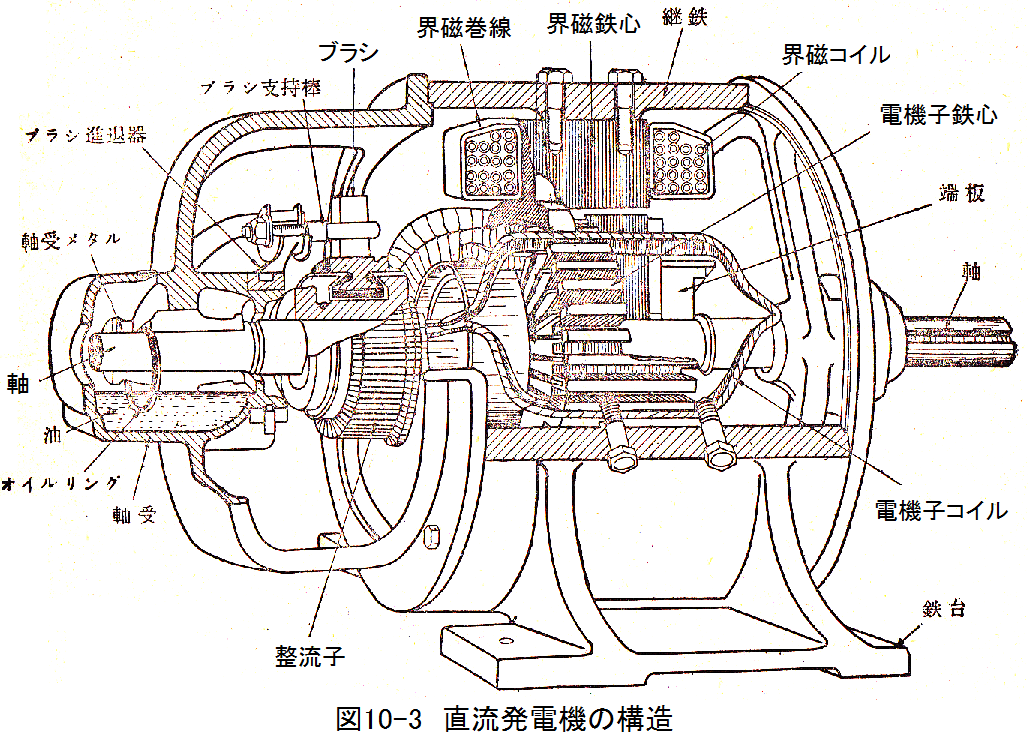
直流発電機の構造を図10-3に示します。図10-1の原理図とはことなり、多くの界磁極数pと多くの巻き線数Zで構成されます。並列結線数aは図からは判断できませんが、2〜pの値をとります。
a=2は波巻き電機子といい高電圧型、あa=pは重巻き電機子といい高電流型に使用されます。
また、大型の発電機では界磁は永久磁石でなく電磁石型が使用されます。
磁コイルの回路方式
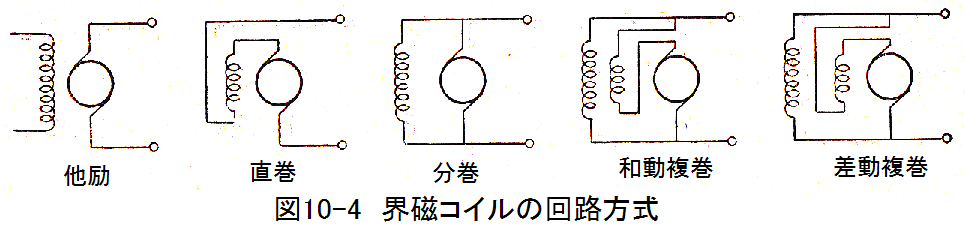
界磁コイルの回路方式は図10-4に示すように、他励、直巻、分巻、和動複巻、差動複巻 等がありますが、分巻が一般的です。
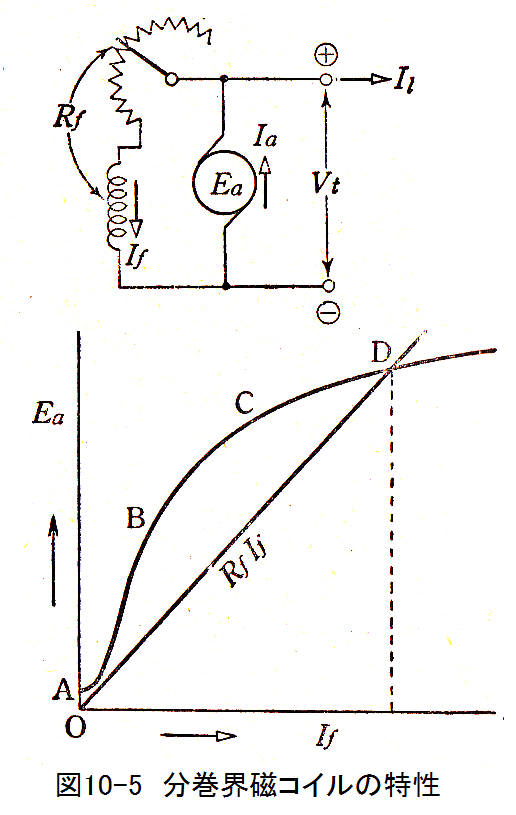
分巻界磁コイルの特性分巻界磁コイルの特性を図10-5に示します。
分巻界磁コイルの電流Ifを横軸、起電力Eaを縦軸にとるとABCDの曲線に示す特性となります。
分巻界磁コイルの抵抗Rfと電流Ifの積はODの直線となります。
起電力EaはD点で飽和します。D点はRfの値できまるため、可変抵抗をつけてRfの値を調整します。
出力電圧Vtは、コイルの抵抗をRa、コイルの電流をIa、出力電流をIｌとすると
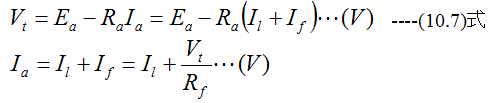
となります。通常Ifは全負荷電流の3〜5%程度となります。上記の式からわかるように負荷が加わると RaIaが増加して端子電圧Vtは低下します。電圧変動率は
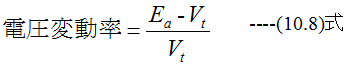
となります。
フレミング左手の法則９章：電磁誘導のフレーミング右手3指の法則は、磁界中の導体の運動による起電力の方向を与えました。今度はフレミング左手の法則です。
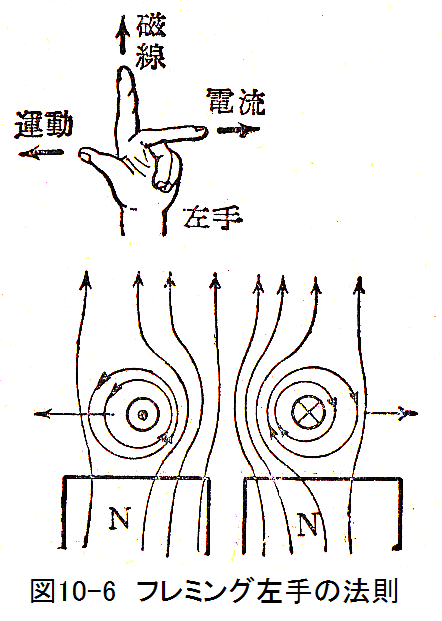
図10-6に示すように磁界中で導体に電流を流すと力を受けます。この方向を知るにはフレミング左手の法則が便利です。
「３指を直角に曲げ、磁界の方向に人差し指を、電流の方向に中指を向けると電線は親指の方向に力を受ける。」
磁束密度の強さをB(Wb/m2)、導体の電流をI(A)、導体の長さをL(m)、力の大きさをF(N)とするならば
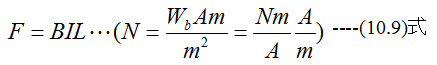
(10.9)式の単位はニュートン（N)となります。
ベクトルの外積フレミング左手の法則をベクトルで一般化すると微小長さds当たりの力ｄFは
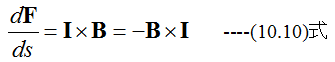
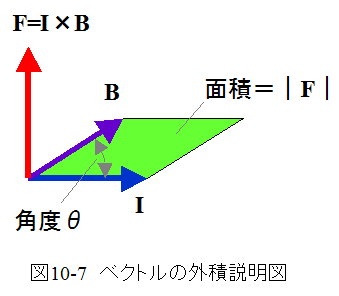
（10.10）式の力F、電流I、磁束密度Bは、方向と大きさを持つ３次元ベクトルです。単位長さ当たりの力Fは電流と磁界の外積として定義できます。
ベクトルの外積の定義は IとHで形成される平行四辺形の面積と大きさが等しく、平行四辺形と垂直な方向ベクトルをベクトルの外積と定義します。
また、正負の方向はIからBに回したとき、右ネジの進む方向を正と定義しています。フレミング左手の法則は右ねじの法則に置き換えることができます。すなわち
「電流Iから磁束密度Bの方向に回したとき、力の方向は右ねじの進む方向となる。」
上記の表現は応用性にとみ、ベクトル解析の定義とも一致するため便利です。なお、ベクトルの外積は積の前後を入れ替えると符号が反転しますので注意が必要です。
直流電動機のトルク直流電動機の構造は直流発電機と同一です。図10-1において、空隙の磁束密度の強さをB(Wb/m2)、コイルの電流をI(A)、コイルの有効長さをL(m)、コイルの平均 半径をR(m)とすれば発生するトルクT(Nm)は
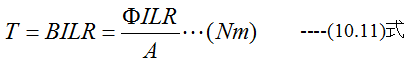
(10.11)式においてΦは１極に発生する磁束、Aは界磁の有効断面積です。
界磁極数をp、コイル総数をZ、コイル並列結線数をaとすれば
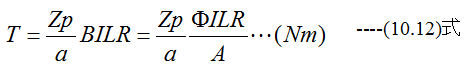
となります。(10.12)式は、コイルが静止状態でのトルクを与えます。負荷トルクが起動トルクより小さい場合は、回転子はトルクにより加速され、しだいに回転数が上昇します。
直流電動機の回転数が上がると、その回転運動により発電が起こります。その起電力は加えられた電圧と逆方向であり逆起電力といいます。その値は
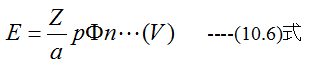
となります。印加電圧と逆起電力は等しくなると、コイルに流れる電流はゼロとなり、トルクがゼロとなります。これが印加電圧における最高回転数となるはずです。実際には摩擦等の損失があり、最高回転数より小さい回転数となるはずです。
したがって、直流電動機は駆動時に大きな電流が流れ、回転数が上がるに従って電流が減少し使用電力が減少します。
詳細の特性については、直流電動機の構造や回路方式に依存しますので、個別に検討する必要があります。
１１章：電界と電位に行く。