電荷の単位電荷量Qは、電流I(A)と時間t(s)で定義されます。
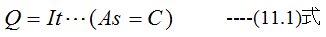
原子はプラスの電荷を持つ原子核とマイナスの電荷をもつ電子で構成されており、電子が不 足するとプラスに帯電し、過剰になるとマイナスに帯電します。
異種の電荷は引力が働き、同種の電荷には反発力が作用します。
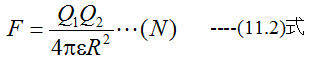
となります。(11.2)式のεを誘電率といいます。
比誘電率真空の誘電率をε0とした場合、比誘電率εｓは
となります。
真空の誘電率ε0の値真空の誘電率をε0、透磁率をμ0、光速をcとすると下記の関係があります。
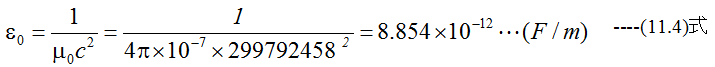
例題11-1大気中に80μCと-50μCが2mを隔てて置かれたとき吸引力はいくらか？空気の比誘電率は1とします。
解答
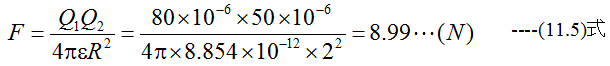
電荷による電界E+Q(C)の電荷からR(m)離れた点Pの電界EはP点に単位電荷を置いたときの力F(N)で定義されます。すなわち
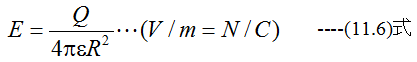
(11.6)式の電界（または電場）の単位は通常V/mを使用します。
電荷による静電ポテンシャルφ（電位）電界Eと静電ポテンシャルφ（電位）の関係は
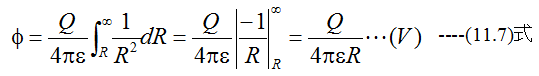
となり、電荷Qに比例し距離Rに反比例することがわかります。
ラプラスの方程式ここで、ベクトル解析による一般式を参考にしてみたいと思います。
静電ポテンシャルφ（電位）の勾配が電界Eとなります。すなわち
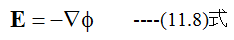
電荷密度ρによる電場Eを与える一般式は
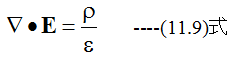
(11.9)式に(11.8)式を代入して
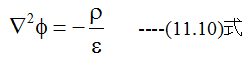
(11.10)式をポアソンの方程式といいます。領域内に電荷が無い場合は
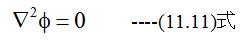
となり、(11.11)式をラプラスの方程式といいます。すなわち、電荷の無い領域において静電ポテンシャルφ（電位）分布はラプラスの方程式を満足することになります。
(11.11)式を満足する解は無限に存在します。従って、解を求めるには厳密に境界条件を決める必要があります。計算の都合で2次元分布とします。2次元のラプラスの方程式は
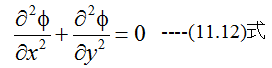
となります。これは偏微分方程式であり、理解しがたいものがありますが、実例を計算 してイメージをつかむ必要があります。
ラプラスの方程式の計算事例基本計算条件は以下とします。
| 項目 | 記号 | 値 |
| 行数（ｊ） | Ni | 21 |
| 列数(j) | Nj | 21 |
| 変化幅 | h | 1 |
| 収束判定値 | e | 0.01 |
| 最大演算回数 | Nc | 200 |
| 演算領域指定 | Ce | -100 |
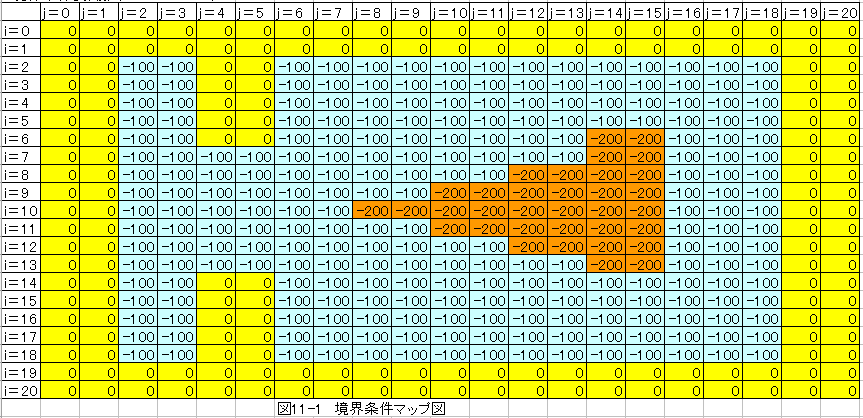
計算結果グラフを下記に示します。
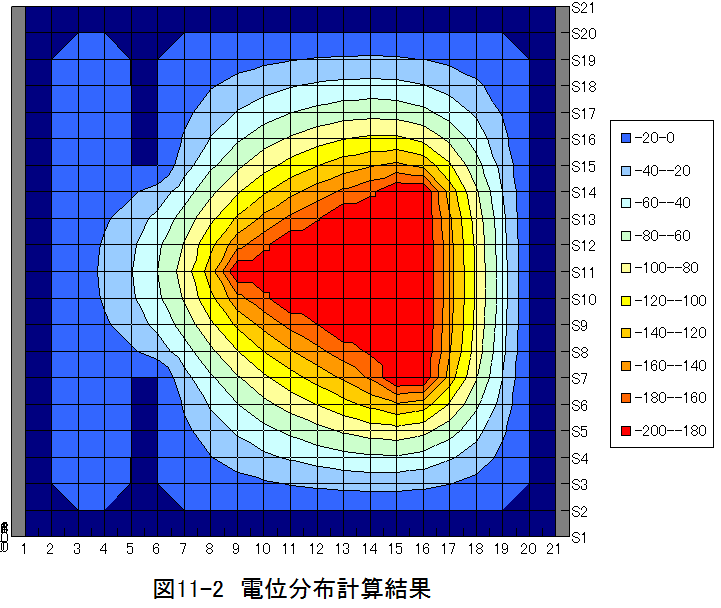
図11-2は空間の電位（電圧）分布を示しています。電界Eは電位の勾配として求めることができます。これから電界Eは 金属の先端部で強く、穴の方向に向かうことがわかります。本計算は２次元の近似計算ですが、３次元ではさら に強調されます。この原理は電子顕微鏡の電子銃や避雷針等に応用されます。
電位分布.xls(フリーソフト)のダウンロード電位分布.xls(フリーソフト)]は下記でダウンロードできます。
ダウンロード後はダブルクリックで解凍してから使用してください。
「電位分布.xls(フリーソフト)」をダウンロードする。
１２章：コンデンサに行く。